人教B版(2019)高中数学选择性必修第一册 1.2.4 二面角word含答案
文档属性
| 名称 | 人教B版(2019)高中数学选择性必修第一册 1.2.4 二面角word含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 594.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 18:19:50 | ||
图片预览




文档简介
1.2.4 二面角
课后篇巩固提升
基础达标练
1.已知ABCD是正方形,E是AB的中点,将△DAE和△CBE分别沿DE,CE折起,使AE与BE重合,A,B两点重合后记为点P,那么二面角P-CD-E的大小为( )
A.30° B.45° C.60° D.90°
答案A
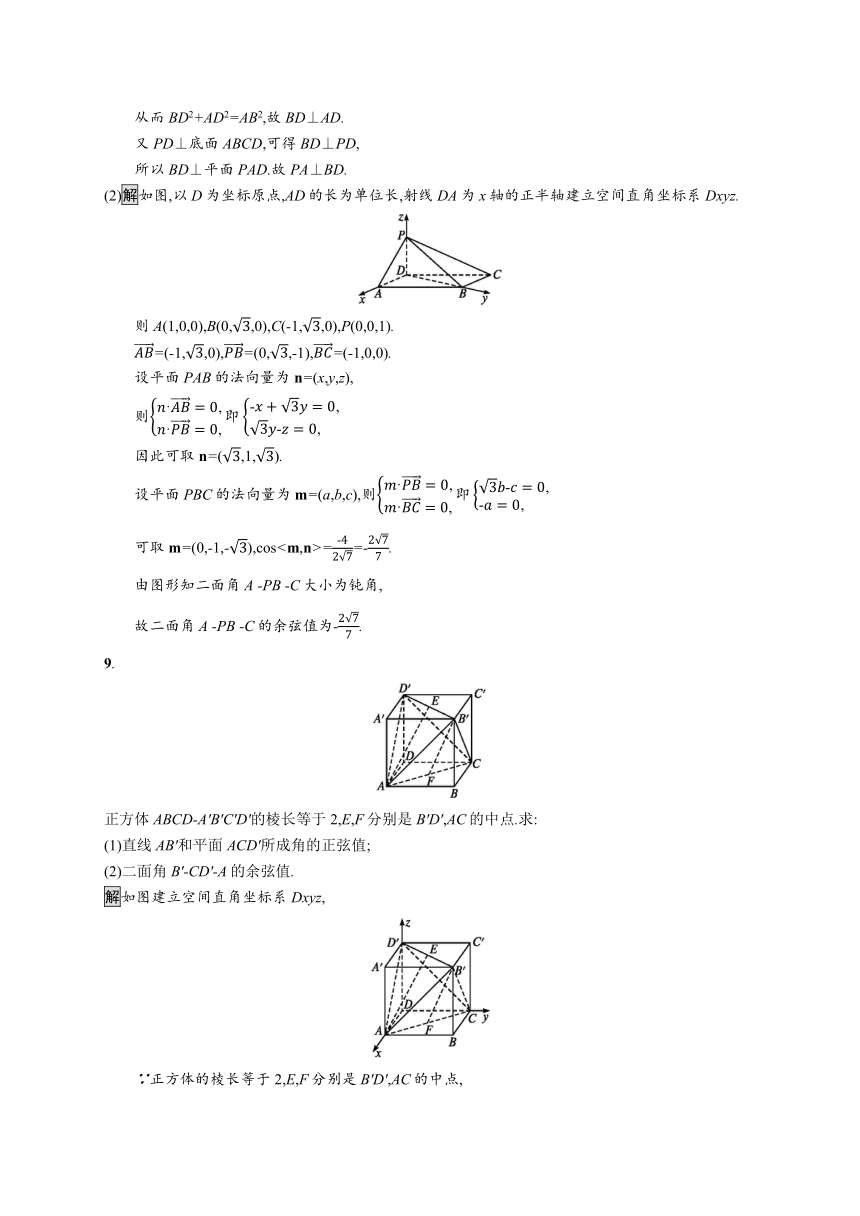
2.如图,设AB为圆锥PO的底面直径,PA为母线,点C在底面圆周上,若△PAB是边长为2的正三角形,且CO⊥AB,则二面角P-AC-B的正弦值是( )
A.6 B.427 C.77 D.7
解析
如图,取AC的中点D,连接OD,PD,
∵PO⊥底面,∴PO⊥AC,
∵OA=OC,D为AC的中点,∴OD⊥AC,
又PO∩OD=O,∴AC⊥平面POD,则AC⊥PD,
∴∠PDO为二面角P-AC-B的平面角.
∵△PAB是边长为2的正三角形,
∴PO=3,OA=OC=1,OD=22,则PD=(3)2+(22)?2 =142.
∴sin∠PDO=POPD=3142=427.
故选B.
答案B
3.正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD所成的角为( )
A.30° B.45° C.60° D.90°
解析如图所示,建立空间直角坐标系,设PA=AB=1,
则A(0,0,0),D(0,1,0),P(0,0,1).
于是AD=(0,1,0),取PD的中点E,则E0,12,12,
∴AE=0,12,12,易知AD是平面PAB的法向量,AE是平面PCD的法向量,
∴cos=22,
∴平面PAB与平面PCD所成的角为45°.
答案B
4.请根据所给的图形,把空白之处填写完整.
(1)直线与平面平行的性质定理(请用符号语言作答).
如图①,已知:a∥α, ,?
求证: .?
(2)平面与平面垂直的性质定理的证明.
如图②,已知:α⊥β,AB∩CD=B,α∩β=CD, , ,?
求证:AB⊥β.
证明:在β内引直线 ,垂足为B,则 是二面角 的平面角,由α⊥β,知 ,又AB⊥CD,BE和CD是β内的两条 直线,所以AB⊥β.?
解(1)已知:a∥α,a?β,α∩β=b,
求证:a∥b.
故答案为a?β,α∩β=b;a∥b.
(2)如图②,已知:α⊥β,AB∩CD=B,
α∩β=CD,AB?α,AB⊥CD,
求证:AB⊥β.
证明:在β内引直线BE⊥CD,垂足为B,
则∠ABE是二面角α-CD-β的平面角,
由α⊥β,知AB⊥BE,又AB⊥CD,
BE和CD是β内的两条相交直线,所以AB⊥β.
故答案为AB?α,AB⊥CD,BE⊥CD,∠ABE,α-CD-β,AB⊥BE,相交.
5.已知正△ABC与正△BCD所在平面垂直,则二面角A-BD-C的正弦值为 .?
解析取BC中点O,连接AO,DO,建立如图所示的空间直角坐标系.
设BC=1,则A0,0,32,B0,-12,0,D32,0,0.
所以OA=0,0,32,
BA=0,12,32,BD=32,12,0.
由于OA=0,0,32为平面BCD的一个法向量,
设平面ABD的法向量为n=(x,y,z),
则n·BA=0,n·BD=0,所以12y+32z=0,32x+12y=0,
取x=1,则y=-3,z=1,所以n=(1,-3,1),
所以cos=55,所以sin=255.
答案255
6.在空间中,已知平面α过(3,0,0)和(0,4,0)及z轴上一点(0,0,a)(a>0),如果平面α与平面xOy所成的角为45°,则a= .?
解析平面xOy的法向量n=(0,0,1),设平面α的法向量为u=(x,y,z),
则-3x+4y=0,-3x+az=0,
即3x=4y=az,取z=1,
则u=a3,a4,1.
而cos=1a29+a216+1=22,又∵a>0,
∴a=125.
答案125
7.
如图所示,已知四棱锥P-ABCD中,底面ABCD是菱形,且PA⊥平面ABCD,PA=AD=AC,点F为PC的中点,求二面角C-BF-D的正切值.
解如图所示,设AC与BD交于O,
连接OF,以O为坐标原点,OB,OC,OF所在直线分别为x轴、y轴、z轴建立空间直角坐标系Oxyz.
设PA=AD=AC=1,则BD=3,
所以O(0,0,0),B32,0,0,F0,0,12,C0,12,0,OC=0,12,0,易知OC为平面BDF的一个法向量.
由BC=-32,12,0,FB=32,0,-12,可得平面BCF的一个法向量为n=(1,3,3),所以cos=217,sin=277,所以tan=233.
8.
如图,在四棱锥P - ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(1)证明:PA⊥BD;
(2)设PD=AD,求二面角A - PB - C的余弦值.
(1)证明因为∠DAB=60°,AB=2AD,由余弦定理得BD=3AD.
从而BD2+AD2=AB2,故BD⊥AD.
又PD⊥底面ABCD,可得BD⊥PD,
所以BD⊥平面PAD.故PA⊥BD.
(2)解如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系Dxyz.
则A(1,0,0),B(0,3,0),C(-1,3,0),P(0,0,1).
AB=(-1,3,0),PB=(0,3,-1),BC=(-1,0,0).
设平面PAB的法向量为n=(x,y,z),
则n·AB=0,n·PB=0,即-x+3y=0,3y-z=0,
因此可取n=(3,1,3).
设平面PBC的法向量为m=(a,b,c),则m·PB=0,m·BC=0,即3b-c=0,-a=0,
可取m=(0,-1,-3),cos=-427=-277.
由图形知二面角A -PB -C大小为钝角,
故二面角A -PB -C的余弦值为-277.
9.
正方体ABCD-A'B'C'D'的棱长等于2,E,F分别是B'D',AC的中点.求:
(1)直线AB'和平面ACD'所成角的正弦值;
(2)二面角B'-CD'-A的余弦值.
解如图建立空间直角坐标系Dxyz,
∵正方体的棱长等于2,E,F分别是B'D',AC的中点,
∴A(2,0,0),B(2,2,0),C(0,2,0),D'(0,0,2),B'(2,2,2),E(1,1,2),F(1,1,0).
(1)AD'=(-2,0,2),AC=(-2,2,0),AB'=(0,2,2),设n=(x',y',z')是平面ACD'的一个法向量,
则由n·AD'=0,n·AC=0,(x',y',z')·(-2,0,2)=0,(x',y',z')·(-2,2,0)=0,
z'=x',y'=x',
取x'=1,得平面ACD'的一个法向量n=(1,1,1),
设直线AB'和平面ACD'所成角的大小为θ,则sin θ=|n·AB'||n||AB'|=|(1,1,1)·(0,2,2)|3×8=63,
∴直线AB'和平面ACD'所成角的正弦值是63.
(2)D'B'=(2,2,0),D'C=(0,2,-2),
设m=(x0,y0,z0)是平面B'CD'的一个法向量,
则由m·D'B'=0,m·D'C=0得x0=-y0,z0=y0,取y0=1得平面B'CD'的一个法向量m=(-1,1,1),
由cos θ=n·m|n|·|m|=(1,1,1)·(-1,1,1)3×3=13,
由图形知二面角B'-CD'-A的大小为锐角.
故二面角B'-CD'-A的余弦值是13.
能力提升练
1.二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=217,则该二面角的大小为( )
A.150° B.45° C.60° D.120°
解析由条件知,CA·AB=0,AB·BD=0,
CD=CA+AB+BD.
∴|CD|2=|CA|2+|AB|2+|BD|2+2CA·AB+2AB·BD+2CA·BD
=62+42+82+2×6×8cos
=(217)2,
∴cos=-12,即=120°,
∴二面角的大小为60°,故选C.
答案C
2.设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点(不含端点).记直线PB与直线AC所成的角为α,直线PB与平面ABC所成的角为β,二面角P-AC-B的平面角为γ,则( )
A.β<γ,α<γ B.β<α,β<γ
C.β<α,γ<α D.α<β,γ<β
解析如图G为AC中点,点V在底面ABC上的投影为点O,则点P在底面ABC上的投影点D在线段AO上,过点D作DE垂直AE,易得PE∥VG,过点P作PF∥AC交VG于点F,过点D作DH∥AC,交BG于点H,则α=∠BPF,β=∠PBD,γ=∠PED,所以cos α=PFPB=EGPB=DHPBβ,因为tan γ=PDED>PDBD=tan β,所以γ>β.故选B.
答案B
3.如图,将菱形ABCD沿对角线BD折起,使得C点至C',E点在线段AC'上,若二面角A-BD-E与二面角E-BD-C'的大小分别为30°和45°,则AEEC'=( )
A.12 B.66 C.22 D.63
解析取BD的中点O,连接AO,EO,C 'O,
∵菱形ABCD沿对角线BD折起,使得C点至C',E点在线段AC'上,
∴C'O⊥BD,AO⊥BD,OC'=OA,
∴BD⊥平面AOC',
∴EO⊥BD,
∵二面角A-BD-E与二面角E-BD-C'的大小分别为30°和45°,
∴∠AOE=30°,∠EOC'=45°,
∵OC'=OA,∴∠OC'E=∠OAE,
由正弦定理得OEsin∠OC'E=EC'sin∠EOC',
OEsin∠OAE=AEsin∠AOE,
∴EC'sin∠EOC'=AEsin∠AOE,
∴AEEC'=sin30°sin45°=1222=22.
故选C.
答案C
4.如图所示,将边长为a的正三角形ABC,沿BC边上的高线AD将△ABC折起.若折起后B,C'间距离为a2,则二面角B-AD-C'的大小为 .?
答案60°
5.如图,在矩形ABCD中,E为线段BC上一动点,现将△ABE沿AE折起得到△AB'E,当二面角B'-AE-D的平面角为120°,点B'在平面ABC上的投影为K,当E从B运动到C,则点K所形成轨迹是 .?
解析过K作KO⊥AE,连接OB',
∵二面角B'-AE-D的平面角为120°,
∴∠B'OK=60°,
∴KO=12B'O,
从而原问题就转化为B'O⊥AE,K为B'O中点, 求K的轨迹长度,如下图,
∵B'O⊥AE,∴O在以AB'为直径的圆上,取AB'中点J,则JK⊥B'K,
所以K点的轨迹是以B'J为直径的圆上的一段弧.
答案一段圆弧
6.如图,在四棱锥P-ABCD中,PC⊥底面ABCD,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
若二面角P-AC-E的余弦值为33,求直线PA与平面EAC所成角的正弦值.
解如图,作CF∥DA,交AB于点F,以C为原点,CF,CD,CP分别为x轴、y轴、z轴正方向,建立空间直角坐标系,
则C(0,0,0),A(1,1,0),B(1,-1,0).
设P(0,0,a)(a>0),则E12,-12,a2,
CA=(1,1,0),CP=(0,0,a),CE=12,-12,a2,
取m=(1,-1,0),则m·CA=m·CP=0,所以m为平面PAC的一个法向量.
设n=(x,y,z)为平面EAC的一个法向量,则n·CA=0,n·CE=0,即x+y=0,x-y+az=0,取x=a,
可得n=(a,-a,-2),
依题意,|cos|=|m·n||m||n|=2a2·2a2+4=33,
则a=1(负值舍去).
于是n=(1,-1,-2),PA=(1,1,-1).
设直线PA与平面EAC所成的角为θ,
则sin θ=|cos|=23,
即直线PA与平面EAC所成角的正弦值为23.
7.
如图,在以A,B,C,D,E,F为顶点的五面体中,平面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
(1)证明:平面ABEF⊥平面EFDC;
(2)求二面角E-BC-A的余弦值.
(1)证明由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC,又AF?平面ABEF,故平面ABEF⊥平面EFDC.
(2)解过D作DG⊥EF,垂足为G,由(1)知DG⊥平面ABEF.以G为坐标原点,GF的方向为x轴正方向,|GF|为单位长,建立如图所示的空间直角坐标系Gxyz.由(1)知∠DFE为二面角D-AF-E的平面角,
故∠DFE=60°,则DF=2,DG=3,
可得A(1,4,0),B(-3,4,0),E(-3,0,0),D(0,0,3).
由已知AB∥EF,所以AB∥平面EFDC,又平面ABCD∩平面EFDC=CD,故AB∥CD,CD∥EF,由BE∥AF,可得BE⊥平面EFDC,
所以∠CEF为二面角C-BE-F的平面角,∠CEF=60°,
从而可得C(-2,0,3).
所以EC=(1,0,3),EB=(0,4,0),AC=(-3,-4,3),AB=(-4,0,0).
设n=(x,y,z)是平面BCE的法向量,则n·EC=0,n·EB=0,
即x+3z=0,4y=0,所以可取n=(3,0,-3).设m=(x1,y1,z1)是平面ABCD的法向量,则m·AC=0,m·AB=0.
同理可取m=(0,3,4),则cos=n·m|n||m|=-21919.
由图形知二面角E-BC-A为钝角,
故二面角E-BC-A的余弦值为-21919.
8.
如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(1)求证:AE⊥BC;
(2)若点N为线段AB的中点,求证:MN∥面ADE;
(3)若BE=4,CE=42,且二面角A-BC-E的大小为45°,求三棱锥C-ABE的体积.
(1)证明∵BM⊥平面ACE,AE?平面ACE,∴BM⊥AE.
∵AE⊥BE,BM∩BE=B,
∴AE⊥平面BCE.
∵BC?平面BCE,
∴AE⊥BC.
(2)证明取DE中点P,连接PM,AP,
∵BC=BE,BM⊥AE,
∴M为CE的中点,
∴MP∥12DC∥AN,且MP=AN,
∴APMN为平行四边形,
∴MN∥AP.
∵MN?平面ADE,AP?平面ADE,
∴MN∥平面ADE.
(3)解由BE=BC=4,CE=42得BC⊥BE.
∵BC⊥AE,AE∩BE=E,
∴BC⊥平面ABE.
∴∠ABE为二面角A-BC-E的平面角.
∴∠ABE=45°.∴AE=BE=4.
∴三棱锥C-ABE的体积13×12×42×4=323.
9.
如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B-EC-C1的正弦值.
(1)证明由已知得,B1C1⊥平面ABB1A1,BE?平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.
(2)解由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,
故AE=AB,AA1=2AB.
以D为坐标原点,DA的方向为x轴正方向,|DA|为单位长,建立如图所示的空间直角坐标系D-xyz,则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),CB=(1,0,0),CE=(1,-1,1),CC1=(0,0,2).
设平面EBC的法向量为n=(x,y,z),则
CB·n=0,CE·n=0,即x=0,x-y+z=0,
所以可取n=(0,-1,-1).
设平面ECC1的法向量为m=(x,y,z),则
CC1·m=0,CE·m=0,即2z=0,x-y+z=0,
所以可取m=(1,1,0).
于是cos=n·m|n||m|=-12.
所以,二面角B-EC-C1的正弦值为32.
10.如图,在长方体ABCD-A1B1C1D中,已知上下两底面为正方形,且边长均为1,侧棱AA1=2,E为BC中点,F为CD中点,G为BB1上一个动点.
(1)确定G点的位置,使得D1E⊥平面AFG;
(2)当D1E⊥平面AFG时,求二面角G-AF-E的平面角的余弦值.
解(1)如图,
分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系Dxyz,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,2).
因为E为BC中点,F为CD中点,所以E12,1,0,F0,12,0.
由题意得D1E⊥AF,D1E⊥AG,设G(1,1,t).
又D1E=12,1,-2,AF=-1,12,0,AG=(0,1,t).
因为D1E⊥平面AFG,则D1E·AF=0,D1E·AG=0,
得1-2t=0,t=12.∴BG=12,
即G为BB1的四等分点.
(2)由题意知,平面AFE的一个法向量为m=(0,0,1),
设平面AFG的法向量n=(x,y,z).
则AF·n=0,AG·n=0,得-x+12y=0,y+12z=0,取x=-1,得n=(-1,-2,4).
∴cos=m·n|m||n|=42121.
由图形知二面角G-AF-E的大小为锐角.
∴二面角G-AF-E的平面角的余弦值为42121.
素养培优练
1.
如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足DQ=12CP,记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E-l-C的大小为β,求证:sin θ=sin αsin β.
(1)解直线l∥平面PAC,证明如下:
连接EF,因为E,F分别是PA,PC的中点,
所以EF∥AC.
又EF?平面ABC,且AC?平面ABC,
所以EF∥平面ABC.
而EF?平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因为l?平面PAC,EF?平面PAC,
所以直线l∥平面PAC.
(2)证明如图,由DQ=12CP,作DQ∥CP,且DQ=12CP.
连接PQ,EF,BE,BF,BD,由(1)可知交线l即为直线BD.
以点C为原点,向量CA,CB,CP所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,设CA=a,CB=b,CP=2c,则有C(0,0,0),A(a,0,0),B(0,b,0),P(0,0,2c),Q(a,b,c),E12a,0,c,F(0,0,c).
于是FE=12a,0,0,QP=(-a,-b,c),BF=(0,-b,c),
所以cos α=|FE·QP||FE||QP| =aa2+b2+c2 ,
从而sin α=1-cos2α=b2+c2 a2+b2+c2 .
又取平面ABC的一个法向量为m=(0,0,1),可得sin θ=|m·QP||m||QP| =ca2+b2+c2 ,
设平面BEF的一个法向量为n=(x,y,z),
所以由n·FE=0,n·BF=0,可得12ax=0,-by+cz=0.取n=(0,c,b).
于是|cos β|=|mn||m|·|n|=bb2+c2 ,
从而sin β=1-cos2β=cb2+c2 .
故sin αsin β=b2+c2 a2+b2+c2 ·cb2+c2 =ca2+b2+c2 =sin θ,即sin θ=sin αsin β.
2.图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小.
(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,
故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.
又因为AB?平面ABC,
所以平面ABC⊥平面BCGE.
(2)解作EH⊥BC,垂足为H.
因为EH?平面BCGE,平面BCGE⊥平面ABC,所以EH⊥平面ABC.
由已知,菱形BCGE的边长为2,∠EBC=60°,可求得BH=1,EH=3.
以H为坐标原点,HC的方向为x轴的正方向,建立如图所示的空间直角坐标系Hxyz,
则A(-1,1,0),C(1,0,0),G(2,0,3),CG=(1,0,3),AC=(2,-1,0).
设平面ACGD的法向量为n=(x,y,z),
则CG·n=0,AC·n=0,即x+3z=0,2x-y=0.
所以可取n=(3,6,-3).
又平面BCGE的法向量可取为m=(0,1,0),
所以cos=n·m|n||m|=32.
由图形知二面角B-CG-A大小为锐角.
因此二面角B-CG-A的大小为30°.
课后篇巩固提升
基础达标练
1.已知ABCD是正方形,E是AB的中点,将△DAE和△CBE分别沿DE,CE折起,使AE与BE重合,A,B两点重合后记为点P,那么二面角P-CD-E的大小为( )
A.30° B.45° C.60° D.90°
答案A
2.如图,设AB为圆锥PO的底面直径,PA为母线,点C在底面圆周上,若△PAB是边长为2的正三角形,且CO⊥AB,则二面角P-AC-B的正弦值是( )
A.6 B.427 C.77 D.7
解析
如图,取AC的中点D,连接OD,PD,
∵PO⊥底面,∴PO⊥AC,
∵OA=OC,D为AC的中点,∴OD⊥AC,
又PO∩OD=O,∴AC⊥平面POD,则AC⊥PD,
∴∠PDO为二面角P-AC-B的平面角.
∵△PAB是边长为2的正三角形,
∴PO=3,OA=OC=1,OD=22,则PD=(3)2+(22)?2 =142.
∴sin∠PDO=POPD=3142=427.
故选B.
答案B
3.正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD所成的角为( )
A.30° B.45° C.60° D.90°
解析如图所示,建立空间直角坐标系,设PA=AB=1,
则A(0,0,0),D(0,1,0),P(0,0,1).
于是AD=(0,1,0),取PD的中点E,则E0,12,12,
∴AE=0,12,12,易知AD是平面PAB的法向量,AE是平面PCD的法向量,
∴cos
∴平面PAB与平面PCD所成的角为45°.
答案B
4.请根据所给的图形,把空白之处填写完整.
(1)直线与平面平行的性质定理(请用符号语言作答).
如图①,已知:a∥α, ,?
求证: .?
(2)平面与平面垂直的性质定理的证明.
如图②,已知:α⊥β,AB∩CD=B,α∩β=CD, , ,?
求证:AB⊥β.
证明:在β内引直线 ,垂足为B,则 是二面角 的平面角,由α⊥β,知 ,又AB⊥CD,BE和CD是β内的两条 直线,所以AB⊥β.?
解(1)已知:a∥α,a?β,α∩β=b,
求证:a∥b.
故答案为a?β,α∩β=b;a∥b.
(2)如图②,已知:α⊥β,AB∩CD=B,
α∩β=CD,AB?α,AB⊥CD,
求证:AB⊥β.
证明:在β内引直线BE⊥CD,垂足为B,
则∠ABE是二面角α-CD-β的平面角,
由α⊥β,知AB⊥BE,又AB⊥CD,
BE和CD是β内的两条相交直线,所以AB⊥β.
故答案为AB?α,AB⊥CD,BE⊥CD,∠ABE,α-CD-β,AB⊥BE,相交.
5.已知正△ABC与正△BCD所在平面垂直,则二面角A-BD-C的正弦值为 .?
解析取BC中点O,连接AO,DO,建立如图所示的空间直角坐标系.
设BC=1,则A0,0,32,B0,-12,0,D32,0,0.
所以OA=0,0,32,
BA=0,12,32,BD=32,12,0.
由于OA=0,0,32为平面BCD的一个法向量,
设平面ABD的法向量为n=(x,y,z),
则n·BA=0,n·BD=0,所以12y+32z=0,32x+12y=0,
取x=1,则y=-3,z=1,所以n=(1,-3,1),
所以cos
答案255
6.在空间中,已知平面α过(3,0,0)和(0,4,0)及z轴上一点(0,0,a)(a>0),如果平面α与平面xOy所成的角为45°,则a= .?
解析平面xOy的法向量n=(0,0,1),设平面α的法向量为u=(x,y,z),
则-3x+4y=0,-3x+az=0,
即3x=4y=az,取z=1,
则u=a3,a4,1.
而cos
∴a=125.
答案125
7.
如图所示,已知四棱锥P-ABCD中,底面ABCD是菱形,且PA⊥平面ABCD,PA=AD=AC,点F为PC的中点,求二面角C-BF-D的正切值.
解如图所示,设AC与BD交于O,
连接OF,以O为坐标原点,OB,OC,OF所在直线分别为x轴、y轴、z轴建立空间直角坐标系Oxyz.
设PA=AD=AC=1,则BD=3,
所以O(0,0,0),B32,0,0,F0,0,12,C0,12,0,OC=0,12,0,易知OC为平面BDF的一个法向量.
由BC=-32,12,0,FB=32,0,-12,可得平面BCF的一个法向量为n=(1,3,3),所以cos
8.
如图,在四棱锥P - ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(1)证明:PA⊥BD;
(2)设PD=AD,求二面角A - PB - C的余弦值.
(1)证明因为∠DAB=60°,AB=2AD,由余弦定理得BD=3AD.
从而BD2+AD2=AB2,故BD⊥AD.
又PD⊥底面ABCD,可得BD⊥PD,
所以BD⊥平面PAD.故PA⊥BD.
(2)解如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系Dxyz.
则A(1,0,0),B(0,3,0),C(-1,3,0),P(0,0,1).
AB=(-1,3,0),PB=(0,3,-1),BC=(-1,0,0).
设平面PAB的法向量为n=(x,y,z),
则n·AB=0,n·PB=0,即-x+3y=0,3y-z=0,
因此可取n=(3,1,3).
设平面PBC的法向量为m=(a,b,c),则m·PB=0,m·BC=0,即3b-c=0,-a=0,
可取m=(0,-1,-3),cos
由图形知二面角A -PB -C大小为钝角,
故二面角A -PB -C的余弦值为-277.
9.
正方体ABCD-A'B'C'D'的棱长等于2,E,F分别是B'D',AC的中点.求:
(1)直线AB'和平面ACD'所成角的正弦值;
(2)二面角B'-CD'-A的余弦值.
解如图建立空间直角坐标系Dxyz,
∵正方体的棱长等于2,E,F分别是B'D',AC的中点,
∴A(2,0,0),B(2,2,0),C(0,2,0),D'(0,0,2),B'(2,2,2),E(1,1,2),F(1,1,0).
(1)AD'=(-2,0,2),AC=(-2,2,0),AB'=(0,2,2),设n=(x',y',z')是平面ACD'的一个法向量,
则由n·AD'=0,n·AC=0,(x',y',z')·(-2,0,2)=0,(x',y',z')·(-2,2,0)=0,
z'=x',y'=x',
取x'=1,得平面ACD'的一个法向量n=(1,1,1),
设直线AB'和平面ACD'所成角的大小为θ,则sin θ=|n·AB'||n||AB'|=|(1,1,1)·(0,2,2)|3×8=63,
∴直线AB'和平面ACD'所成角的正弦值是63.
(2)D'B'=(2,2,0),D'C=(0,2,-2),
设m=(x0,y0,z0)是平面B'CD'的一个法向量,
则由m·D'B'=0,m·D'C=0得x0=-y0,z0=y0,取y0=1得平面B'CD'的一个法向量m=(-1,1,1),
由cos θ=n·m|n|·|m|=(1,1,1)·(-1,1,1)3×3=13,
由图形知二面角B'-CD'-A的大小为锐角.
故二面角B'-CD'-A的余弦值是13.
能力提升练
1.二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=217,则该二面角的大小为( )
A.150° B.45° C.60° D.120°
解析由条件知,CA·AB=0,AB·BD=0,
CD=CA+AB+BD.
∴|CD|2=|CA|2+|AB|2+|BD|2+2CA·AB+2AB·BD+2CA·BD
=62+42+82+2×6×8cos
=(217)2,
∴cos
∴二面角的大小为60°,故选C.
答案C
2.设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点(不含端点).记直线PB与直线AC所成的角为α,直线PB与平面ABC所成的角为β,二面角P-AC-B的平面角为γ,则( )
A.β<γ,α<γ B.β<α,β<γ
C.β<α,γ<α D.α<β,γ<β
解析如图G为AC中点,点V在底面ABC上的投影为点O,则点P在底面ABC上的投影点D在线段AO上,过点D作DE垂直AE,易得PE∥VG,过点P作PF∥AC交VG于点F,过点D作DH∥AC,交BG于点H,则α=∠BPF,β=∠PBD,γ=∠PED,所以cos α=PFPB=EGPB=DHPB
答案B
3.如图,将菱形ABCD沿对角线BD折起,使得C点至C',E点在线段AC'上,若二面角A-BD-E与二面角E-BD-C'的大小分别为30°和45°,则AEEC'=( )
A.12 B.66 C.22 D.63
解析取BD的中点O,连接AO,EO,C 'O,
∵菱形ABCD沿对角线BD折起,使得C点至C',E点在线段AC'上,
∴C'O⊥BD,AO⊥BD,OC'=OA,
∴BD⊥平面AOC',
∴EO⊥BD,
∵二面角A-BD-E与二面角E-BD-C'的大小分别为30°和45°,
∴∠AOE=30°,∠EOC'=45°,
∵OC'=OA,∴∠OC'E=∠OAE,
由正弦定理得OEsin∠OC'E=EC'sin∠EOC',
OEsin∠OAE=AEsin∠AOE,
∴EC'sin∠EOC'=AEsin∠AOE,
∴AEEC'=sin30°sin45°=1222=22.
故选C.
答案C
4.如图所示,将边长为a的正三角形ABC,沿BC边上的高线AD将△ABC折起.若折起后B,C'间距离为a2,则二面角B-AD-C'的大小为 .?
答案60°
5.如图,在矩形ABCD中,E为线段BC上一动点,现将△ABE沿AE折起得到△AB'E,当二面角B'-AE-D的平面角为120°,点B'在平面ABC上的投影为K,当E从B运动到C,则点K所形成轨迹是 .?
解析过K作KO⊥AE,连接OB',
∵二面角B'-AE-D的平面角为120°,
∴∠B'OK=60°,
∴KO=12B'O,
从而原问题就转化为B'O⊥AE,K为B'O中点, 求K的轨迹长度,如下图,
∵B'O⊥AE,∴O在以AB'为直径的圆上,取AB'中点J,则JK⊥B'K,
所以K点的轨迹是以B'J为直径的圆上的一段弧.
答案一段圆弧
6.如图,在四棱锥P-ABCD中,PC⊥底面ABCD,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
若二面角P-AC-E的余弦值为33,求直线PA与平面EAC所成角的正弦值.
解如图,作CF∥DA,交AB于点F,以C为原点,CF,CD,CP分别为x轴、y轴、z轴正方向,建立空间直角坐标系,
则C(0,0,0),A(1,1,0),B(1,-1,0).
设P(0,0,a)(a>0),则E12,-12,a2,
CA=(1,1,0),CP=(0,0,a),CE=12,-12,a2,
取m=(1,-1,0),则m·CA=m·CP=0,所以m为平面PAC的一个法向量.
设n=(x,y,z)为平面EAC的一个法向量,则n·CA=0,n·CE=0,即x+y=0,x-y+az=0,取x=a,
可得n=(a,-a,-2),
依题意,|cos
则a=1(负值舍去).
于是n=(1,-1,-2),PA=(1,1,-1).
设直线PA与平面EAC所成的角为θ,
则sin θ=|cos
即直线PA与平面EAC所成角的正弦值为23.
7.
如图,在以A,B,C,D,E,F为顶点的五面体中,平面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
(1)证明:平面ABEF⊥平面EFDC;
(2)求二面角E-BC-A的余弦值.
(1)证明由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC,又AF?平面ABEF,故平面ABEF⊥平面EFDC.
(2)解过D作DG⊥EF,垂足为G,由(1)知DG⊥平面ABEF.以G为坐标原点,GF的方向为x轴正方向,|GF|为单位长,建立如图所示的空间直角坐标系Gxyz.由(1)知∠DFE为二面角D-AF-E的平面角,
故∠DFE=60°,则DF=2,DG=3,
可得A(1,4,0),B(-3,4,0),E(-3,0,0),D(0,0,3).
由已知AB∥EF,所以AB∥平面EFDC,又平面ABCD∩平面EFDC=CD,故AB∥CD,CD∥EF,由BE∥AF,可得BE⊥平面EFDC,
所以∠CEF为二面角C-BE-F的平面角,∠CEF=60°,
从而可得C(-2,0,3).
所以EC=(1,0,3),EB=(0,4,0),AC=(-3,-4,3),AB=(-4,0,0).
设n=(x,y,z)是平面BCE的法向量,则n·EC=0,n·EB=0,
即x+3z=0,4y=0,所以可取n=(3,0,-3).设m=(x1,y1,z1)是平面ABCD的法向量,则m·AC=0,m·AB=0.
同理可取m=(0,3,4),则cos
由图形知二面角E-BC-A为钝角,
故二面角E-BC-A的余弦值为-21919.
8.
如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(1)求证:AE⊥BC;
(2)若点N为线段AB的中点,求证:MN∥面ADE;
(3)若BE=4,CE=42,且二面角A-BC-E的大小为45°,求三棱锥C-ABE的体积.
(1)证明∵BM⊥平面ACE,AE?平面ACE,∴BM⊥AE.
∵AE⊥BE,BM∩BE=B,
∴AE⊥平面BCE.
∵BC?平面BCE,
∴AE⊥BC.
(2)证明取DE中点P,连接PM,AP,
∵BC=BE,BM⊥AE,
∴M为CE的中点,
∴MP∥12DC∥AN,且MP=AN,
∴APMN为平行四边形,
∴MN∥AP.
∵MN?平面ADE,AP?平面ADE,
∴MN∥平面ADE.
(3)解由BE=BC=4,CE=42得BC⊥BE.
∵BC⊥AE,AE∩BE=E,
∴BC⊥平面ABE.
∴∠ABE为二面角A-BC-E的平面角.
∴∠ABE=45°.∴AE=BE=4.
∴三棱锥C-ABE的体积13×12×42×4=323.
9.
如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B-EC-C1的正弦值.
(1)证明由已知得,B1C1⊥平面ABB1A1,BE?平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.
(2)解由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,
故AE=AB,AA1=2AB.
以D为坐标原点,DA的方向为x轴正方向,|DA|为单位长,建立如图所示的空间直角坐标系D-xyz,则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),CB=(1,0,0),CE=(1,-1,1),CC1=(0,0,2).
设平面EBC的法向量为n=(x,y,z),则
CB·n=0,CE·n=0,即x=0,x-y+z=0,
所以可取n=(0,-1,-1).
设平面ECC1的法向量为m=(x,y,z),则
CC1·m=0,CE·m=0,即2z=0,x-y+z=0,
所以可取m=(1,1,0).
于是cos
所以,二面角B-EC-C1的正弦值为32.
10.如图,在长方体ABCD-A1B1C1D中,已知上下两底面为正方形,且边长均为1,侧棱AA1=2,E为BC中点,F为CD中点,G为BB1上一个动点.
(1)确定G点的位置,使得D1E⊥平面AFG;
(2)当D1E⊥平面AFG时,求二面角G-AF-E的平面角的余弦值.
解(1)如图,
分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系Dxyz,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,2).
因为E为BC中点,F为CD中点,所以E12,1,0,F0,12,0.
由题意得D1E⊥AF,D1E⊥AG,设G(1,1,t).
又D1E=12,1,-2,AF=-1,12,0,AG=(0,1,t).
因为D1E⊥平面AFG,则D1E·AF=0,D1E·AG=0,
得1-2t=0,t=12.∴BG=12,
即G为BB1的四等分点.
(2)由题意知,平面AFE的一个法向量为m=(0,0,1),
设平面AFG的法向量n=(x,y,z).
则AF·n=0,AG·n=0,得-x+12y=0,y+12z=0,取x=-1,得n=(-1,-2,4).
∴cos
由图形知二面角G-AF-E的大小为锐角.
∴二面角G-AF-E的平面角的余弦值为42121.
素养培优练
1.
如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足DQ=12CP,记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E-l-C的大小为β,求证:sin θ=sin αsin β.
(1)解直线l∥平面PAC,证明如下:
连接EF,因为E,F分别是PA,PC的中点,
所以EF∥AC.
又EF?平面ABC,且AC?平面ABC,
所以EF∥平面ABC.
而EF?平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因为l?平面PAC,EF?平面PAC,
所以直线l∥平面PAC.
(2)证明如图,由DQ=12CP,作DQ∥CP,且DQ=12CP.
连接PQ,EF,BE,BF,BD,由(1)可知交线l即为直线BD.
以点C为原点,向量CA,CB,CP所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,设CA=a,CB=b,CP=2c,则有C(0,0,0),A(a,0,0),B(0,b,0),P(0,0,2c),Q(a,b,c),E12a,0,c,F(0,0,c).
于是FE=12a,0,0,QP=(-a,-b,c),BF=(0,-b,c),
所以cos α=|FE·QP||FE||QP| =aa2+b2+c2 ,
从而sin α=1-cos2α=b2+c2 a2+b2+c2 .
又取平面ABC的一个法向量为m=(0,0,1),可得sin θ=|m·QP||m||QP| =ca2+b2+c2 ,
设平面BEF的一个法向量为n=(x,y,z),
所以由n·FE=0,n·BF=0,可得12ax=0,-by+cz=0.取n=(0,c,b).
于是|cos β|=|mn||m|·|n|=bb2+c2 ,
从而sin β=1-cos2β=cb2+c2 .
故sin αsin β=b2+c2 a2+b2+c2 ·cb2+c2 =ca2+b2+c2 =sin θ,即sin θ=sin αsin β.
2.图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小.
(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,
故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.
又因为AB?平面ABC,
所以平面ABC⊥平面BCGE.
(2)解作EH⊥BC,垂足为H.
因为EH?平面BCGE,平面BCGE⊥平面ABC,所以EH⊥平面ABC.
由已知,菱形BCGE的边长为2,∠EBC=60°,可求得BH=1,EH=3.
以H为坐标原点,HC的方向为x轴的正方向,建立如图所示的空间直角坐标系Hxyz,
则A(-1,1,0),C(1,0,0),G(2,0,3),CG=(1,0,3),AC=(2,-1,0).
设平面ACGD的法向量为n=(x,y,z),
则CG·n=0,AC·n=0,即x+3z=0,2x-y=0.
所以可取n=(3,6,-3).
又平面BCGE的法向量可取为m=(0,1,0),
所以cos
由图形知二面角B-CG-A大小为锐角.
因此二面角B-CG-A的大小为30°.
