人教版高中物理选修3-3 10.5热力学第二定律的微观解释(共33张PPT)
文档属性
| 名称 | 人教版高中物理选修3-3 10.5热力学第二定律的微观解释(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-09 06:58:50 | ||
图片预览










文档简介
(共33张PPT)
热力学第二定律的微观解释
教学目标
了解有序和无序是相对的??
知道宏观态与微观态,知道宏观态对应的微观态的数目与无序程度的对应关系?
知道熵的概念,初步了解熵是描述系统无序程度的物理量。了解熵增加原理,知道它是热力学第二定律的另一种表述?
能用熵增加原理解释生活中的一些现象
教学重点
教学难点
了解热力学第二定律的微观意义
.?
了解熵的概念,知道熵是反映系统无序程度的物理量
对熵和熵增加原理的解释
前情回顾
热力学第二定律揭示了什么规律?
热力学第二定律揭示了一切与热现象有关的宏观自然过程都是不可逆的
系统的宏观表现源于组成系统的微观粒子的统计规律
本节从微观角度说明为什么涉及热运动的宏观过程会有一定的方向性
按花色及大小排列
我们说它是有序的
有序和无序
洗牌后变为无序
有序和无序
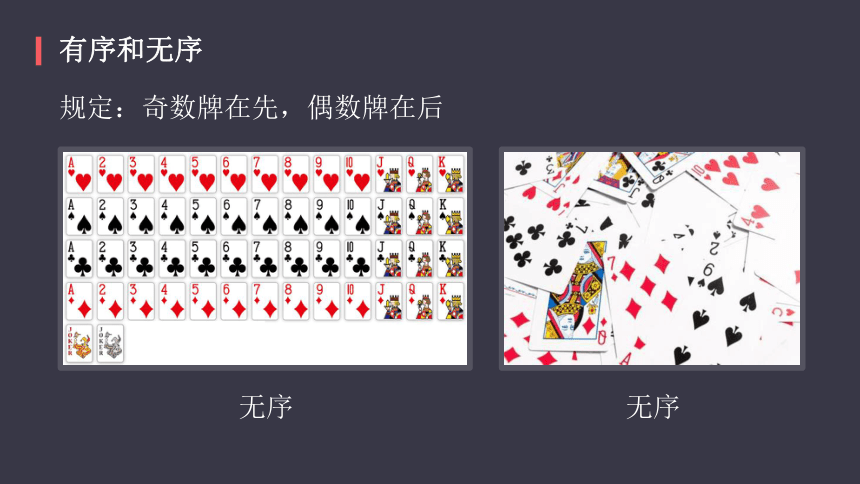
规定:奇数牌在先,偶数牌在后
无序
无序
有序和无序
有序:只要确定了某种规则,符合这个规则的就叫做有序。
无序:不符合某种确定规则的称为无序。
有序和无序
无序意味着各处都一样,平均、没有差别,有序则相反。
有序和无序是相对的
宏观态:符合某种规定、规则的状态,叫做热力学系统的宏观态。
宏观态和微观态
微观态:在宏观状态下,符合另外的规定、规则的状态叫做这个宏观态的微观态。
系统的宏观态所对应的微观态的多少表现为宏观态无序程度的大小
如果一个“宏观态”对应的“微观态”比较多,就说这个“宏观态”是比较无序的
;同时也决定了宏观过程的方向性——从有序到无序。
下面从统计观点探讨过程的不可逆性微观意义,并由此深入认识第二定律的本质
不可逆性的微观意义
不可逆过程的统计性质(以气体自由膨胀为例)
一个被隔板分为A、B相等两部分的容器,装有4个涂以不同颜色分子
气体向真空扩散
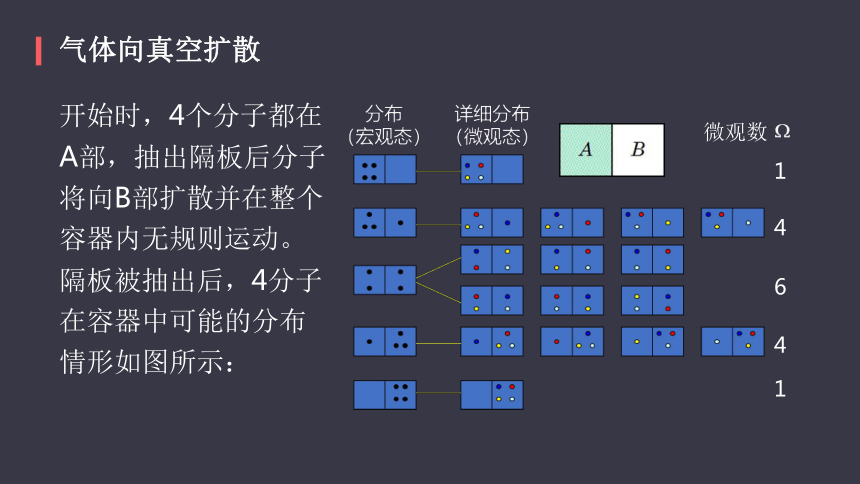
开始时,4个分子都在A部,抽出隔板后分子将向B部扩散并在整个容器内无规则运动。隔板被抽出后,4分子在容器中可能的分布情形如图所示:
微观数
1
4
4
1
6
气体向真空扩散
此数值极小,意味着此事件永远不会发生。从任何实际操作的意义上说,不可能发生此类事件。
气体向真空扩散
对单个分子或少量分子来说,它们扩散到B部的过程原则上是可逆的。
对大量分子组成的宏观系统来说,它们向B部自由膨胀的宏观过程实际上是不可逆的。这就是宏观过程的不可逆性在微观上的统计解释。
气体向真空扩散
左边一列的各种分布仅指出A、B两边各有几个分子,代表的是系统可能的宏观态。
中间各列是详细的分布,具体指明了这个或那个分子各处于A或B哪一边,代表的是系统的任意一个微观态。
4个分子在容器中的分布对应5种宏观态
一种宏观态对应若干种微观态
不同的宏观态对应的微观态数不同
均匀分布对应的微观态数最多。
全部退回A边仅对应一种微观态。
在一定的宏观条件下,各种可能的宏观态中哪一种是实际所观测到的?
气体向真空扩散
热力学第二定律的统计意义
统计物理基本假定—等几率原理:
对于孤立系,各种微观态出现的可能性(或几率)是相等的。
各种宏观态不是等几率的。那种宏观态包含的微观态数多,这种宏观态出现的可能性就大。
热力学第二定律的统计意义
在气体向真空扩散的例子中,均匀分布这种宏观态,相应的微观态最多,热力学几率最大,实际观测到的可能性或几率最大。
所以,实际观测到的总是均匀分布这种宏观态。即系统最后所达到的平衡态。
热力学第二定律的统计意义
热力学第二定律的统计表述:孤立系统内部所发生的过程总是从包含微观态数少的宏观态向包含微观态数多的宏观态过渡,从热力学几率小的状态向热力学几率大的状态过渡。
①自然过程总是向着使系统热力学几率增大的方向进行。
②一切自然过程总是沿着无序性增大的方向进行。
注意:微观状态数最大的平衡态状态是最混乱、最无序的状态。
热力学第二定律的统计意义
热力学第二定律的适用范围
①适用于宏观过程,对微观过程不适用
如布朗运动
②孤立系统,有限范围
对整个宇宙不适用
热力学第二定律的微观意义
对于一个热力学系统,如果处于非平衡态,我们认为它处于有序的状态,如果处于平衡态,我们认为它处于无序的状态。
在热力学中,序:区分度。
热力学第二定律的微观意义:
一切自然过程总是沿着无序性增大的方向进行
“熵”是什么?
熵与熵增加原理
“熵”是德国物理学家克劳修斯在1850年创造的一个术语,他用熵来表示任何一种能量在空间分布的均匀程度。能量分布得越均匀,熵就越大。如果对于我们所考虑的那个系统来说,能量完全均匀地分布,那么这个系统的熵就达到最大值。
简单的说,“熵”就是微观粒子的无序程度、能量差别的消除程度。
在克劳修斯看来,在一个封闭的系统中,运动总是从有序到无序发展的
熵与熵增加原理
比如,把一块冰糖放入水中,结果整杯水都甜了。这就是说,糖分子的运动扩展到了整杯水中,它们的运动变得更加无序了。
对于一个封闭的系统,能量差也总是倾向于消除的。
比如,有水位差的两个水库,如果把它们连接起来,那么,重力就会使一个水库的水面降低,而使另一个水库的水面升高,直到两个水库的水面均等,势能取平为止。
克劳修斯总结说,自然界中的一个普遍规律是:运动总是从有序到无序,能量的差异总是倾向变成均等,也即“熵将随着时间而增大”。
熵和系统内能一样都是一个状态函数,仅由系统的状态决定。
从分子运动论的观点来看,熵是分子热运动无序(混乱)程度的定量量度。
熵与熵增加原理
一个系统的熵是随着系统状态的变化而变化的。在自然过程中,系统的熵是增加的。
熵与熵增加原理
在绝热过程或孤立系统中,熵是增加的,叫做熵增加原理。对于其它情况,系统的熵可能增加,也可能减小。
从微观的角度看,热力学第二定律是一个统计规律:一个孤立系统总是从熵小的状态向熵大的状态发展,而熵值较大代表着较为无序,所以自发的宏观过程总是向无序程度更大的方向发展。
一个物体在粗糙的平面上滑动,最后停止。系统的熵如何变化?
熵与熵增加原理的理解
因为物体由于受到摩擦力而停止运动,其动能变为系统的内能,增加了系统分子无规则运动的程度,使得无规则运动加强,也就是系统的无序程度增加了,所以系统的熵增加。?
一个密闭的容器内有稀薄气体,在容器上开一小口,外部的空气就会流入容器,在气体流入过程中,容器内靠近开口处的空气密度暂时变得比内部大,以下说法正确的是(?
?
?
)
熵与熵增加原理的理解
A.此时容器内气体处于一个不平衡状态,是一个最无序的状态
B.外界的影响破坏了容器内气体的平衡
C.上面事实说明热力学第二定律只适用于封闭系统
D.对一个开放系统并不一定是最无序的分布
BCD
一个封闭的方盒内有两个隔板,把方盒隔成了三个小房间,每个小房间内有2个球,球上各有一个字,小房间内球上的字恰好组成如图所示的三个词(从左向右念)。振动方盒,球在小房间内的左右位置可以变换。??
问题与练习
(1)图中6个球同时排列成这三个词的概率是多少?
(2)取去其中一个隔板,振动方盒,6个球能同时排列成这三个词的概率又是多少?
(3)把链各个隔板全部取去,摇动方盒,6个球能同时排列成这三个词的概率又是多少?
(4)在这个封闭的方盒内,取消隔板让小球充分地运动,其无序性是增大了还是减小了?
(4)无序性增大
成语“覆水难收”指的是一盆水泼出后是不可能再回到盆中的。请从不同宏观态所对应的微观态数目不同这个角度,解释为什么水不会自发地聚到盆中。
问题与练习
“覆水难收”是中国古代的一句成语,字面意思是泼出去的水无法收回,表示事已定居,不可挽回。盛在盆中的水,水分子分布情况受盆的容积、形状的限制,对应的微观态较少;而泼出去的水,水分子的分布受制约较少,对应额微观态较多。根据熵增加原理,自发过程进行的方向总是朝着熵增加,即无序性增大的方向进行,因此泼出去的水(无序性大)不可能自发地回到盆中(无序性小)。
无序意味着各处都一样,平均、没有差别,有序则相反。
总结
有序和无序是相对的。
热力学第二定律的统计表述:孤立系统内部所发生的过程总是从包含微观态数少的宏观态向包含微观态数多的宏观态过渡,从热力学几率小的状态向热力学几率大的状态过渡。
注意:微观状态数最大的平衡态状态是最混乱、最无序的状态。
在绝热过程或孤立系统中,熵是增加的,叫做熵增加原理。对于其它情况,系统的熵可能增加,也可能减小。
【分析】
【解答】
【点评】
练习
【分析】
【解答】
【点评】
练习
【分析】
【解答】
【点评】
练习
热力学第二定律的微观解释
教学目标
了解有序和无序是相对的??
知道宏观态与微观态,知道宏观态对应的微观态的数目与无序程度的对应关系?
知道熵的概念,初步了解熵是描述系统无序程度的物理量。了解熵增加原理,知道它是热力学第二定律的另一种表述?
能用熵增加原理解释生活中的一些现象
教学重点
教学难点
了解热力学第二定律的微观意义
.?
了解熵的概念,知道熵是反映系统无序程度的物理量
对熵和熵增加原理的解释
前情回顾
热力学第二定律揭示了什么规律?
热力学第二定律揭示了一切与热现象有关的宏观自然过程都是不可逆的
系统的宏观表现源于组成系统的微观粒子的统计规律
本节从微观角度说明为什么涉及热运动的宏观过程会有一定的方向性
按花色及大小排列
我们说它是有序的
有序和无序
洗牌后变为无序
有序和无序
规定:奇数牌在先,偶数牌在后
无序
无序
有序和无序
有序:只要确定了某种规则,符合这个规则的就叫做有序。
无序:不符合某种确定规则的称为无序。
有序和无序
无序意味着各处都一样,平均、没有差别,有序则相反。
有序和无序是相对的
宏观态:符合某种规定、规则的状态,叫做热力学系统的宏观态。
宏观态和微观态
微观态:在宏观状态下,符合另外的规定、规则的状态叫做这个宏观态的微观态。
系统的宏观态所对应的微观态的多少表现为宏观态无序程度的大小
如果一个“宏观态”对应的“微观态”比较多,就说这个“宏观态”是比较无序的
;同时也决定了宏观过程的方向性——从有序到无序。
下面从统计观点探讨过程的不可逆性微观意义,并由此深入认识第二定律的本质
不可逆性的微观意义
不可逆过程的统计性质(以气体自由膨胀为例)
一个被隔板分为A、B相等两部分的容器,装有4个涂以不同颜色分子
气体向真空扩散
开始时,4个分子都在A部,抽出隔板后分子将向B部扩散并在整个容器内无规则运动。隔板被抽出后,4分子在容器中可能的分布情形如图所示:
微观数
1
4
4
1
6
气体向真空扩散
此数值极小,意味着此事件永远不会发生。从任何实际操作的意义上说,不可能发生此类事件。
气体向真空扩散
对单个分子或少量分子来说,它们扩散到B部的过程原则上是可逆的。
对大量分子组成的宏观系统来说,它们向B部自由膨胀的宏观过程实际上是不可逆的。这就是宏观过程的不可逆性在微观上的统计解释。
气体向真空扩散
左边一列的各种分布仅指出A、B两边各有几个分子,代表的是系统可能的宏观态。
中间各列是详细的分布,具体指明了这个或那个分子各处于A或B哪一边,代表的是系统的任意一个微观态。
4个分子在容器中的分布对应5种宏观态
一种宏观态对应若干种微观态
不同的宏观态对应的微观态数不同
均匀分布对应的微观态数最多。
全部退回A边仅对应一种微观态。
在一定的宏观条件下,各种可能的宏观态中哪一种是实际所观测到的?
气体向真空扩散
热力学第二定律的统计意义
统计物理基本假定—等几率原理:
对于孤立系,各种微观态出现的可能性(或几率)是相等的。
各种宏观态不是等几率的。那种宏观态包含的微观态数多,这种宏观态出现的可能性就大。
热力学第二定律的统计意义
在气体向真空扩散的例子中,均匀分布这种宏观态,相应的微观态最多,热力学几率最大,实际观测到的可能性或几率最大。
所以,实际观测到的总是均匀分布这种宏观态。即系统最后所达到的平衡态。
热力学第二定律的统计意义
热力学第二定律的统计表述:孤立系统内部所发生的过程总是从包含微观态数少的宏观态向包含微观态数多的宏观态过渡,从热力学几率小的状态向热力学几率大的状态过渡。
①自然过程总是向着使系统热力学几率增大的方向进行。
②一切自然过程总是沿着无序性增大的方向进行。
注意:微观状态数最大的平衡态状态是最混乱、最无序的状态。
热力学第二定律的统计意义
热力学第二定律的适用范围
①适用于宏观过程,对微观过程不适用
如布朗运动
②孤立系统,有限范围
对整个宇宙不适用
热力学第二定律的微观意义
对于一个热力学系统,如果处于非平衡态,我们认为它处于有序的状态,如果处于平衡态,我们认为它处于无序的状态。
在热力学中,序:区分度。
热力学第二定律的微观意义:
一切自然过程总是沿着无序性增大的方向进行
“熵”是什么?
熵与熵增加原理
“熵”是德国物理学家克劳修斯在1850年创造的一个术语,他用熵来表示任何一种能量在空间分布的均匀程度。能量分布得越均匀,熵就越大。如果对于我们所考虑的那个系统来说,能量完全均匀地分布,那么这个系统的熵就达到最大值。
简单的说,“熵”就是微观粒子的无序程度、能量差别的消除程度。
在克劳修斯看来,在一个封闭的系统中,运动总是从有序到无序发展的
熵与熵增加原理
比如,把一块冰糖放入水中,结果整杯水都甜了。这就是说,糖分子的运动扩展到了整杯水中,它们的运动变得更加无序了。
对于一个封闭的系统,能量差也总是倾向于消除的。
比如,有水位差的两个水库,如果把它们连接起来,那么,重力就会使一个水库的水面降低,而使另一个水库的水面升高,直到两个水库的水面均等,势能取平为止。
克劳修斯总结说,自然界中的一个普遍规律是:运动总是从有序到无序,能量的差异总是倾向变成均等,也即“熵将随着时间而增大”。
熵和系统内能一样都是一个状态函数,仅由系统的状态决定。
从分子运动论的观点来看,熵是分子热运动无序(混乱)程度的定量量度。
熵与熵增加原理
一个系统的熵是随着系统状态的变化而变化的。在自然过程中,系统的熵是增加的。
熵与熵增加原理
在绝热过程或孤立系统中,熵是增加的,叫做熵增加原理。对于其它情况,系统的熵可能增加,也可能减小。
从微观的角度看,热力学第二定律是一个统计规律:一个孤立系统总是从熵小的状态向熵大的状态发展,而熵值较大代表着较为无序,所以自发的宏观过程总是向无序程度更大的方向发展。
一个物体在粗糙的平面上滑动,最后停止。系统的熵如何变化?
熵与熵增加原理的理解
因为物体由于受到摩擦力而停止运动,其动能变为系统的内能,增加了系统分子无规则运动的程度,使得无规则运动加强,也就是系统的无序程度增加了,所以系统的熵增加。?
一个密闭的容器内有稀薄气体,在容器上开一小口,外部的空气就会流入容器,在气体流入过程中,容器内靠近开口处的空气密度暂时变得比内部大,以下说法正确的是(?
?
?
)
熵与熵增加原理的理解
A.此时容器内气体处于一个不平衡状态,是一个最无序的状态
B.外界的影响破坏了容器内气体的平衡
C.上面事实说明热力学第二定律只适用于封闭系统
D.对一个开放系统并不一定是最无序的分布
BCD
一个封闭的方盒内有两个隔板,把方盒隔成了三个小房间,每个小房间内有2个球,球上各有一个字,小房间内球上的字恰好组成如图所示的三个词(从左向右念)。振动方盒,球在小房间内的左右位置可以变换。??
问题与练习
(1)图中6个球同时排列成这三个词的概率是多少?
(2)取去其中一个隔板,振动方盒,6个球能同时排列成这三个词的概率又是多少?
(3)把链各个隔板全部取去,摇动方盒,6个球能同时排列成这三个词的概率又是多少?
(4)在这个封闭的方盒内,取消隔板让小球充分地运动,其无序性是增大了还是减小了?
(4)无序性增大
成语“覆水难收”指的是一盆水泼出后是不可能再回到盆中的。请从不同宏观态所对应的微观态数目不同这个角度,解释为什么水不会自发地聚到盆中。
问题与练习
“覆水难收”是中国古代的一句成语,字面意思是泼出去的水无法收回,表示事已定居,不可挽回。盛在盆中的水,水分子分布情况受盆的容积、形状的限制,对应的微观态较少;而泼出去的水,水分子的分布受制约较少,对应额微观态较多。根据熵增加原理,自发过程进行的方向总是朝着熵增加,即无序性增大的方向进行,因此泼出去的水(无序性大)不可能自发地回到盆中(无序性小)。
无序意味着各处都一样,平均、没有差别,有序则相反。
总结
有序和无序是相对的。
热力学第二定律的统计表述:孤立系统内部所发生的过程总是从包含微观态数少的宏观态向包含微观态数多的宏观态过渡,从热力学几率小的状态向热力学几率大的状态过渡。
注意:微观状态数最大的平衡态状态是最混乱、最无序的状态。
在绝热过程或孤立系统中,熵是增加的,叫做熵增加原理。对于其它情况,系统的熵可能增加,也可能减小。
【分析】
【解答】
【点评】
练习
【分析】
【解答】
【点评】
练习
【分析】
【解答】
【点评】
练习
