人教版数学九年级下册 26.1.2 反比例函数的图象和性质(第2课时)(共25张PPT)
文档属性
| 名称 | 人教版数学九年级下册 26.1.2 反比例函数的图象和性质(第2课时)(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 07:43:43 | ||
图片预览



文档简介
(共25张PPT)
二、学习目标
1、会用描点法画反比例函数的图象
.
2.结合图象分析并掌握反比例函数的性质
3.体会函数的三种表示方法,领会数形结合的思想方法.
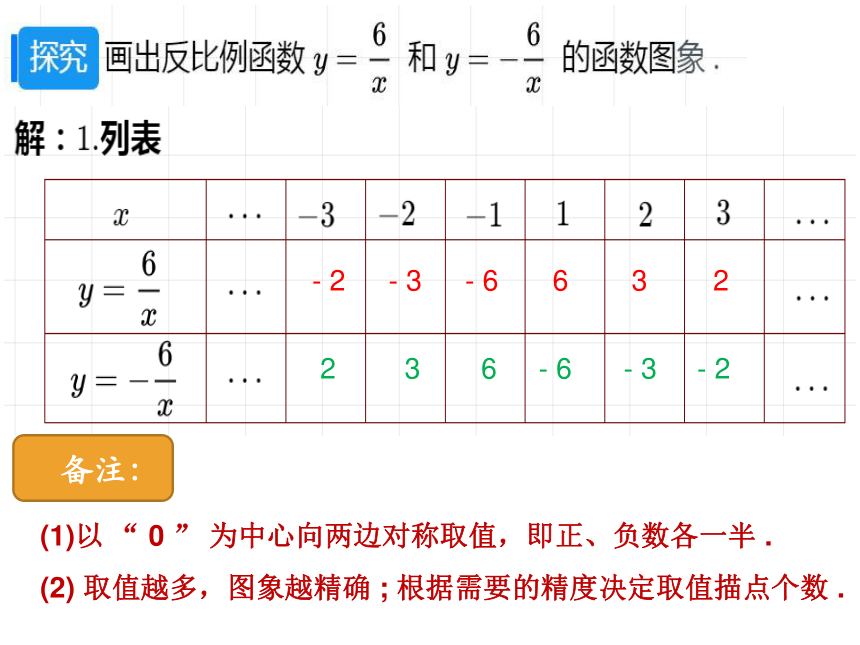
回顾旧知,探寻图象的画法
活动1
探究一:复习提问,引入新知
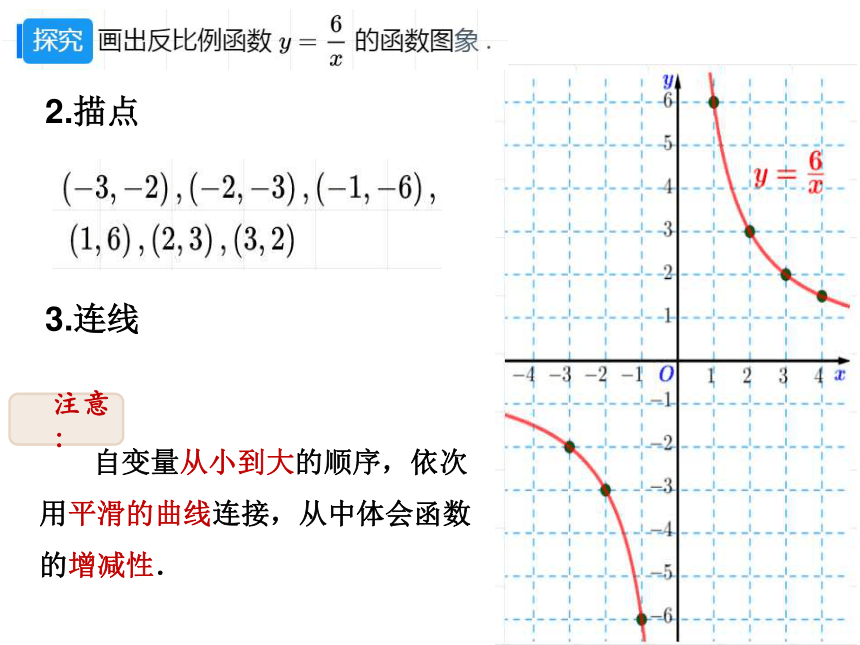
2.描点
3.连线
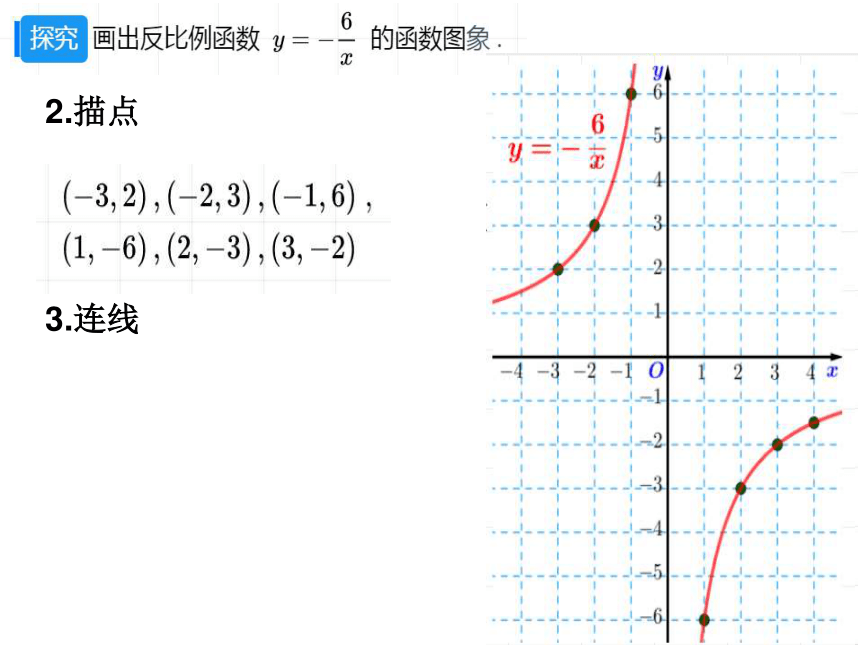
2.描点
3.连线
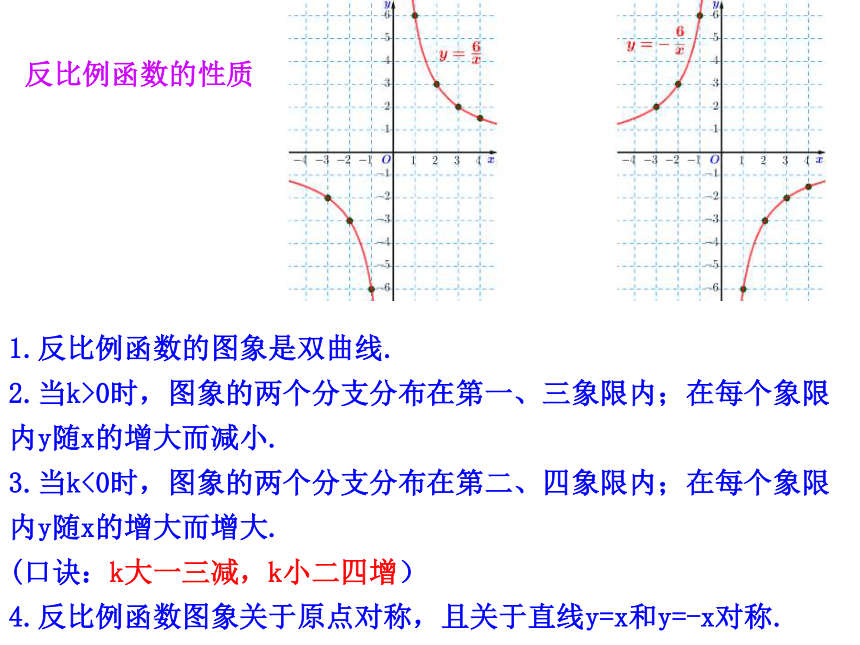
反比例函数的性质
1.反比例函数的图象是双曲线.
2.当k>0时,图象的两个分支分布在第一、三象限内;在每个象限内y随x的增大而减小.
3.当k<0时,图象的两个分支分布在第二、四象限内;在每个象限内y随x的增大而增大.
(口诀:k大一三减,k小二四增)
4.反比例函数图象关于原点对称,且关于直线y=x和y=-x对称.
位置
增减性
位置
增减性
y=kx
(
k≠0
)
直线
双曲线
一、三象限
y随x的增大而增大
一、三象限
每个象限内,
y随x的增大而减小
二、四象限
二、四象限
y随x的增大而减小
每个象限内,
y随x的增大而增大
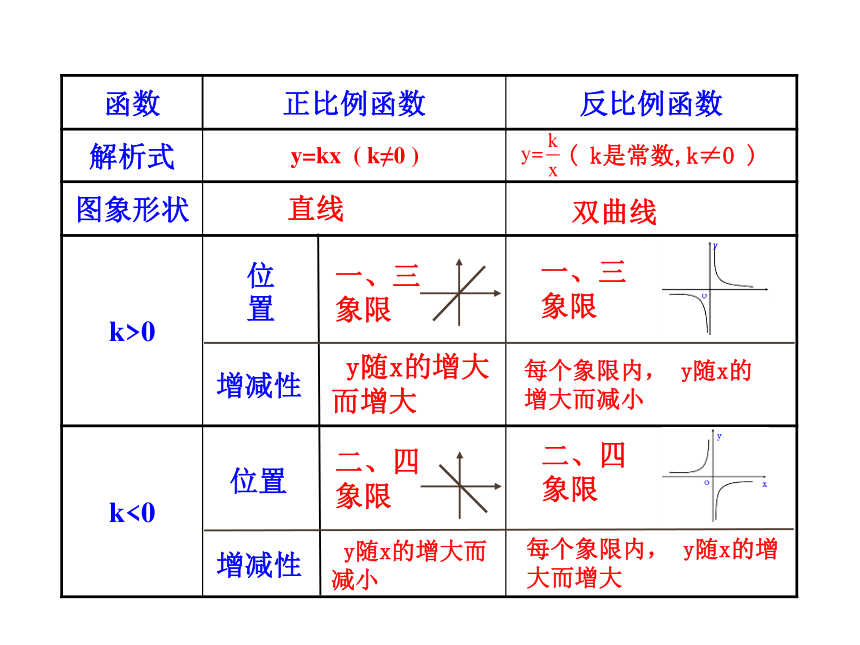
函数
正比例函数
反比例函数
解析式
图象形状
k>0
k<0
解得:
k=12
∴这个反比例函数的表达式为
∵k>0
∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。
∵图象过点A(2,6)
解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。
∵函数的图象在第一、第三象限
∴ m-5>0
解得
m>5
(2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,
∴当a>a′时b<b′
练习:
A
B
y1
>y2
y3
>y1>y2
考察函数
的图象,当x=-2时,y=
___
,当x<-2时,y的取值范围是
_____
;当y﹥-1时,x的取值范围是
_________,当y<-1时,x的取值范围是
______.
-1
-1X<-2或x>0
-21.函数y=kx-k
与
在同一条直角坐标系中的
图象可能是
:
D
这是反比例函数及一次函数的性质的综合运用,可以采用
排除法;也可以让学生分两种情况(k>0和k<0)讨论。
反比例和一次函数综合练习
2.已知k<0,则函数
y1=kx,
y2=
在同一坐标系中的图象大致是
(
)
D
3.
已知k>0,则函数
y1=kx+k与y2=
在同一坐标系中的图象大致是
(
)
C
面积性质(一)
面积性质
根据象限确定k的符号
(m,n)
1
思考:
=
面积性质(三)
二、学习目标
1、会用描点法画反比例函数的图象
.
2.结合图象分析并掌握反比例函数的性质
3.体会函数的三种表示方法,领会数形结合的思想方法.
回顾旧知,探寻图象的画法
活动1
探究一:复习提问,引入新知
2.描点
3.连线
2.描点
3.连线
反比例函数的性质
1.反比例函数的图象是双曲线.
2.当k>0时,图象的两个分支分布在第一、三象限内;在每个象限内y随x的增大而减小.
3.当k<0时,图象的两个分支分布在第二、四象限内;在每个象限内y随x的增大而增大.
(口诀:k大一三减,k小二四增)
4.反比例函数图象关于原点对称,且关于直线y=x和y=-x对称.
位置
增减性
位置
增减性
y=kx
(
k≠0
)
直线
双曲线
一、三象限
y随x的增大而增大
一、三象限
每个象限内,
y随x的增大而减小
二、四象限
二、四象限
y随x的增大而减小
每个象限内,
y随x的增大而增大
函数
正比例函数
反比例函数
解析式
图象形状
k>0
k<0
解得:
k=12
∴这个反比例函数的表达式为
∵k>0
∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。
∵图象过点A(2,6)
解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。
∵函数的图象在第一、第三象限
∴ m-5>0
解得
m>5
(2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,
∴当a>a′时b<b′
练习:
A
B
y1
>y2
y3
>y1>y2
考察函数
的图象,当x=-2时,y=
___
,当x<-2时,y的取值范围是
_____
;当y﹥-1时,x的取值范围是
_________,当y<-1时,x的取值范围是
______.
-1
-1
-2
与
在同一条直角坐标系中的
图象可能是
:
D
这是反比例函数及一次函数的性质的综合运用,可以采用
排除法;也可以让学生分两种情况(k>0和k<0)讨论。
反比例和一次函数综合练习
2.已知k<0,则函数
y1=kx,
y2=
在同一坐标系中的图象大致是
(
)
D
3.
已知k>0,则函数
y1=kx+k与y2=
在同一坐标系中的图象大致是
(
)
C
面积性质(一)
面积性质
根据象限确定k的符号
(m,n)
1
思考:
=
面积性质(三)
