人教数学八年级上册课件:15.2.3整数指数幂(16张ppt)
文档属性
| 名称 | 人教数学八年级上册课件:15.2.3整数指数幂(16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
15.2分式的运算(第3课时)
1、当n为正整数时,an表示的实际意义是什么?
2、正整数指数幂的运算性质有哪些?
问题1
am
中指数m
可以是负整数吗?如果可以,那么负整数指数幂am
表示什么?
请同学们试着用同样的方法计算
看看能得到什么结果?
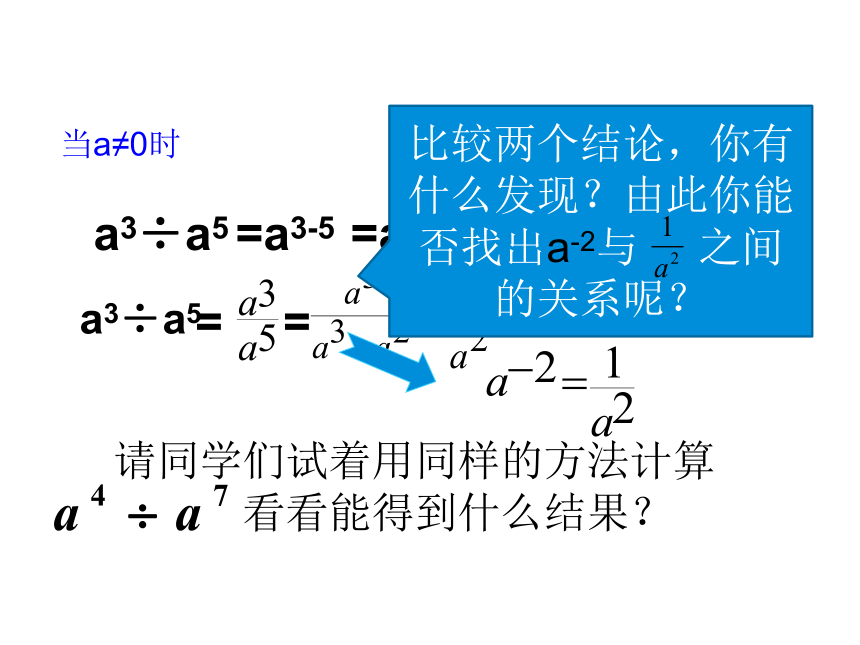
a3÷a5
a3÷a5
=a3-5
=a-2
=
=
当a≠0时
规定:
一般地,当n是正整数时,
例如:
这就是说:(当a≠0时)a-n是an的倒数。
例1 填空:
(1)
2-1=___,
3-1=___,
x-1=___.
(2)
(-2)
-1=___,
(-3)
-1=___,
(-x)
-1=___.
(3)
4-2=___,
(-4)
-2=___,
-4-2=
.
2
例2、把下列各式转化为只含有正整数指数幂的形式
1、a-3
2、x3y-2
3、2(m+n)-2
例3、利用负整指数幂把下列各式化成不含分母的式子
3、
思考:
引入负整数指数后,
(m、n是正整数)这条性质能否扩大到
m、n是全体整数的情形?
填空:
(1)
(2)
(3)
你有何发现,与同伴交流一下
类似地,请同学们分组举例验证,看看前面提到的其他正整数指数幂的运算性质在整数指数幂范围内是否还适用.
归纳:整数指数幂的运算性质:
(1)
(m、n是整数)
(2)
(m、n是整数)
(3)
(n是整数)
(4)
(a≠0,m、n是整数)
(5)
(b≠0,n是整数)
(6)a0=1
(a≠0)
例1
计算:
.
(1)
;
(2)
;
(3)
;
(4)
.
(1)
(2)
(3)
课堂练习:
1、本节课你有什么收获?
.
2.
你还有那些想法?
我收获
我快乐
课余思考:
1、当x为何值时,有意义?
2、当x为何值时,值为零?
3、当X为何值时,值为正?
15.2分式的运算(第3课时)
1、当n为正整数时,an表示的实际意义是什么?
2、正整数指数幂的运算性质有哪些?
问题1
am
中指数m
可以是负整数吗?如果可以,那么负整数指数幂am
表示什么?
请同学们试着用同样的方法计算
看看能得到什么结果?
a3÷a5
a3÷a5
=a3-5
=a-2
=
=
当a≠0时
规定:
一般地,当n是正整数时,
例如:
这就是说:(当a≠0时)a-n是an的倒数。
例1 填空:
(1)
2-1=___,
3-1=___,
x-1=___.
(2)
(-2)
-1=___,
(-3)
-1=___,
(-x)
-1=___.
(3)
4-2=___,
(-4)
-2=___,
-4-2=
.
2
例2、把下列各式转化为只含有正整数指数幂的形式
1、a-3
2、x3y-2
3、2(m+n)-2
例3、利用负整指数幂把下列各式化成不含分母的式子
3、
思考:
引入负整数指数后,
(m、n是正整数)这条性质能否扩大到
m、n是全体整数的情形?
填空:
(1)
(2)
(3)
你有何发现,与同伴交流一下
类似地,请同学们分组举例验证,看看前面提到的其他正整数指数幂的运算性质在整数指数幂范围内是否还适用.
归纳:整数指数幂的运算性质:
(1)
(m、n是整数)
(2)
(m、n是整数)
(3)
(n是整数)
(4)
(a≠0,m、n是整数)
(5)
(b≠0,n是整数)
(6)a0=1
(a≠0)
例1
计算:
.
(1)
;
(2)
;
(3)
;
(4)
.
(1)
(2)
(3)
课堂练习:
1、本节课你有什么收获?
.
2.
你还有那些想法?
我收获
我快乐
课余思考:
1、当x为何值时,有意义?
2、当x为何值时,值为零?
3、当X为何值时,值为正?
