人教版数学八年级上册课件:11.2.2三角形的外角(18张PPT)
文档属性
| 名称 | 人教版数学八年级上册课件:11.2.2三角形的外角(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
11.2.2
三角形的外角
课件说明
学习目标:
1.理解三角形的外角的概念.
2.掌握三角形的一个外角等于与它不相邻的两个内
角的和.
学习重点:
掌握三角形的一个外角等于与它不相邻的两个内角
的和.
一、巧设情境,引入新课
1、上节课我们证明了三角形内角和定理,请大家看图完成以下两题:
(1)图中∠A、∠B、∠C是三角的
;
(2)∠A+∠B+∠C=
C
B
A
三角形的外角
定义:
三角形的一边与另一边的延长线所组成的角,
叫做三角形的外角。
特征:
(1)
顶点在三角形的一个顶点上.
(2)
一条边是三角形的一边.
(3)
另一条边是三角形某条边的延长线.
2
P
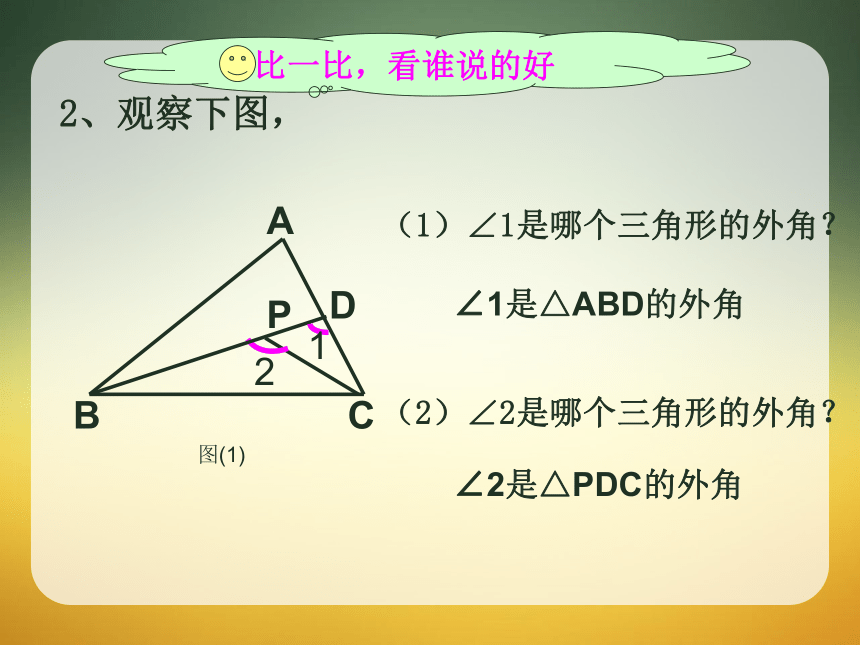
2、观察下图,
图(1)
(1)∠1是哪个三角形的外角?
(2)∠2是哪个三角形的外角?
∠1是△ABD的外角
∠2是△PDC的外角
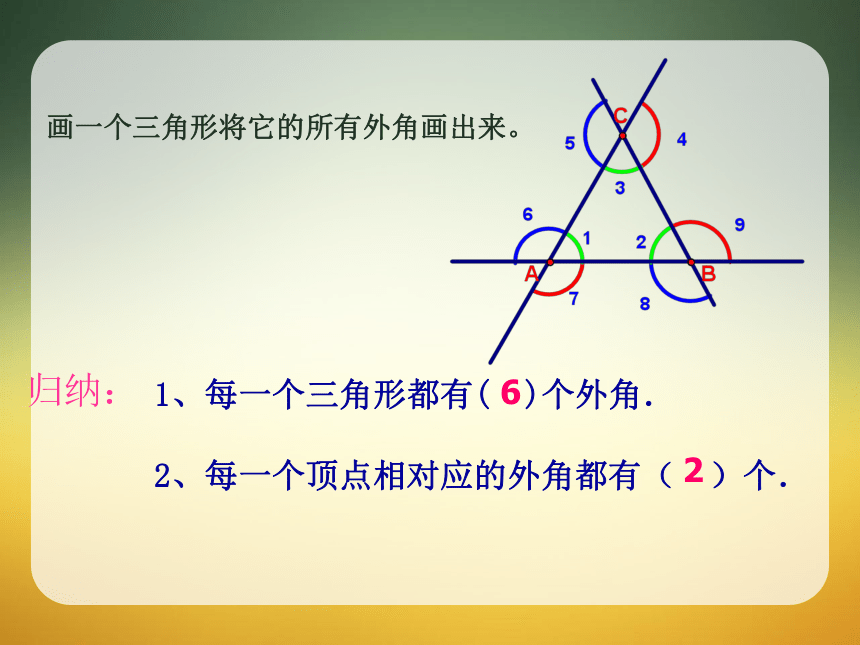
画一个三角形将它的所有外角画出来。
1、每一个三角形都有(
)个外角.
2、每一个顶点相对应的外角都有(
)个.
归纳:
6
2
(1)外角∠ACD与∠ACB有什么特殊关系?
∠ACD+∠ACB=180°
(2)∠ACD与∠A,
∠B由什么关系?
想一想:
D
D
∵
∠ACD+
∠ACB=180°
又∵∠A+
∠B+
∠ACB=180°
∴
∠A+
∠B=∠ACD
证明:
∴
∠ACD
=180
°-∠ACB
∴
∠A+∠B
=180
°-∠ACB
(邻补角的定义)
(三角形内角和定理)
(等量代换)
已知:ABC
证明:∠ACD=
∠B+
∠
A
思考
(等式的性质)
(等式的性质)
1
(CE//BA)
A
E
C
B
D
画平行线法
D
证明:过C作CE//BA
A
B
C
∠1=
∠B
∠2=
∠A
∠1+
∠2=
∠A+
∠B
即∠ACD=
∠A+
∠B
三角形的一个外角等于与它不相邻的两个内角的和
画平行线法
三角形的一个外角大于与它不相邻的任何一个内角。
说出下列各图中∠1的度数。
初试身手
探索2
如图,∵∠1+_______=180°
∠2+_______=180°
∠3+______=180°
∴∠1+
∠2+∠3+______+______+______=____°
∴
+
+
=
°
又∵∠1+
∠2+
∠3
=_____°
∠BAE
∠CBF
∠ACD
180
540
1
2
3
360
归纳结论:
三角形的外角和等于360°
课堂小结
这节课你有哪些收获?
1、三角形的外角性质.
2、三角形的外角和.
1、如图所示,AB//CD,∠A=37°,
∠C=63°,那么∠F等于(
)
F
A
B
E
C
D
A、
26°
B、
63°
C、
37°
D、
60°
2.如图(2),∠A、∠DOE和∠BEC的大小关系(
)
求∠A+
∠B+
∠C+
∠D+
∠E的度数
3、国旗上的数学
2、如图,求∠A+
∠B+
∠C+
∠D+
∠E+
∠F的度数。(选做题)
A
B
C
D
E
F
作业:1、习题11.2
5、6题
11.2.2
三角形的外角
课件说明
学习目标:
1.理解三角形的外角的概念.
2.掌握三角形的一个外角等于与它不相邻的两个内
角的和.
学习重点:
掌握三角形的一个外角等于与它不相邻的两个内角
的和.
一、巧设情境,引入新课
1、上节课我们证明了三角形内角和定理,请大家看图完成以下两题:
(1)图中∠A、∠B、∠C是三角的
;
(2)∠A+∠B+∠C=
C
B
A
三角形的外角
定义:
三角形的一边与另一边的延长线所组成的角,
叫做三角形的外角。
特征:
(1)
顶点在三角形的一个顶点上.
(2)
一条边是三角形的一边.
(3)
另一条边是三角形某条边的延长线.
2
P
2、观察下图,
图(1)
(1)∠1是哪个三角形的外角?
(2)∠2是哪个三角形的外角?
∠1是△ABD的外角
∠2是△PDC的外角
画一个三角形将它的所有外角画出来。
1、每一个三角形都有(
)个外角.
2、每一个顶点相对应的外角都有(
)个.
归纳:
6
2
(1)外角∠ACD与∠ACB有什么特殊关系?
∠ACD+∠ACB=180°
(2)∠ACD与∠A,
∠B由什么关系?
想一想:
D
D
∵
∠ACD+
∠ACB=180°
又∵∠A+
∠B+
∠ACB=180°
∴
∠A+
∠B=∠ACD
证明:
∴
∠ACD
=180
°-∠ACB
∴
∠A+∠B
=180
°-∠ACB
(邻补角的定义)
(三角形内角和定理)
(等量代换)
已知:ABC
证明:∠ACD=
∠B+
∠
A
思考
(等式的性质)
(等式的性质)
1
(CE//BA)
A
E
C
B
D
画平行线法
D
证明:过C作CE//BA
A
B
C
∠1=
∠B
∠2=
∠A
∠1+
∠2=
∠A+
∠B
即∠ACD=
∠A+
∠B
三角形的一个外角等于与它不相邻的两个内角的和
画平行线法
三角形的一个外角大于与它不相邻的任何一个内角。
说出下列各图中∠1的度数。
初试身手
探索2
如图,∵∠1+_______=180°
∠2+_______=180°
∠3+______=180°
∴∠1+
∠2+∠3+______+______+______=____°
∴
+
+
=
°
又∵∠1+
∠2+
∠3
=_____°
∠BAE
∠CBF
∠ACD
180
540
1
2
3
360
归纳结论:
三角形的外角和等于360°
课堂小结
这节课你有哪些收获?
1、三角形的外角性质.
2、三角形的外角和.
1、如图所示,AB//CD,∠A=37°,
∠C=63°,那么∠F等于(
)
F
A
B
E
C
D
A、
26°
B、
63°
C、
37°
D、
60°
2.如图(2),∠A、∠DOE和∠BEC的大小关系(
)
求∠A+
∠B+
∠C+
∠D+
∠E的度数
3、国旗上的数学
2、如图,求∠A+
∠B+
∠C+
∠D+
∠E+
∠F的度数。(选做题)
A
B
C
D
E
F
作业:1、习题11.2
5、6题
