人教版数学八年级上册14.1.2幂的乘方课件(17张ppt)
文档属性
| 名称 | 人教版数学八年级上册14.1.2幂的乘方课件(17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 10:54:44 | ||
图片预览





文档简介
(共17张PPT)
人教版八年级(上册)
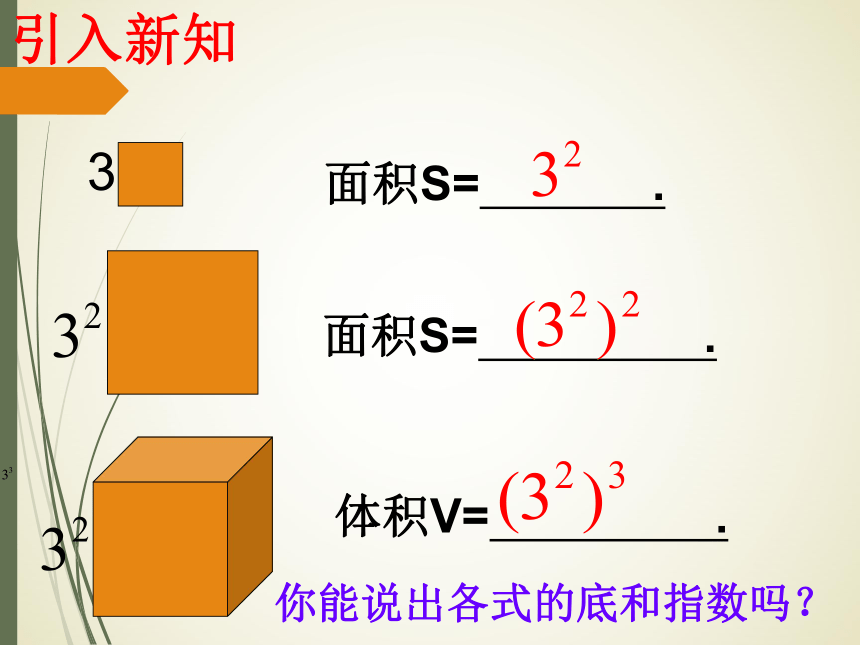
3
面积S=
.
面积S=
.
体积V=
.
你能说出各式的底和指数吗?
引入新知?
(32)3=32×32×32=3(
);
(a2)3=a2×a2×a2=a(
).
(am)3=am·am·am=a(
)
(m是正整数)
根据乘方的意义及同底数幂的乘法填空,看
看计算的结果有什么规律:
这几道题有什么共同的特点呢?计算的结果有什么规律吗?
观察:
(2)
(3)
猜想:
探索新知
?
(a2)3=
a6
(1)
探索新知
?
幂的乘方,
(am)n
=
amn
幂的乘方
底数不变,指数相乘
(m,n都是正整数
)
底数不变,指数相乘.
幂的乘方法则:
归纳结论?
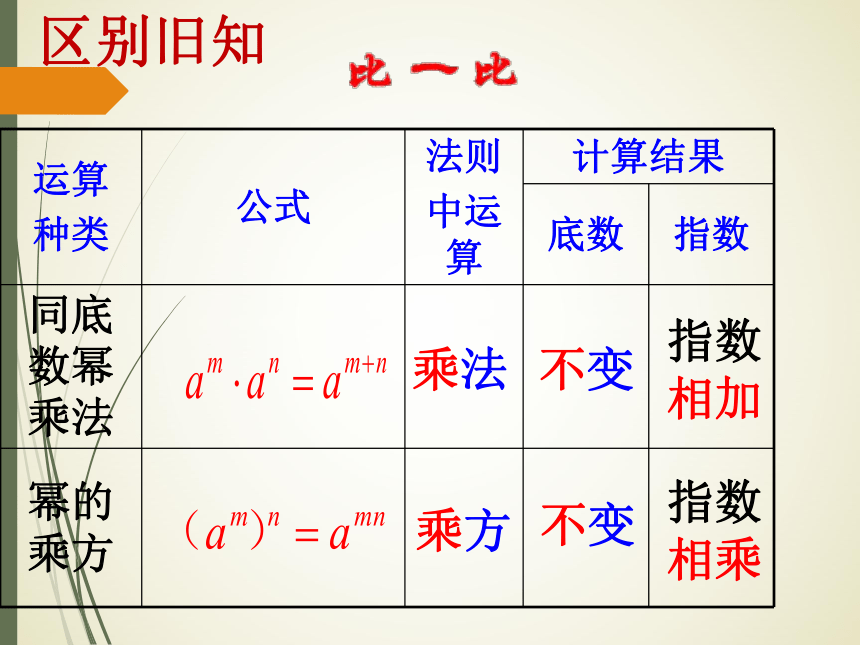
乘法
乘方
不变
不变
指数
相加
指数
相乘
区别旧知
运算
种类
公式
法则
中运算
计算结果
底数
指数
同底数幂乘法
幂的乘方
(1)
(103)5
(2)
(a4)4
(3)
(am)2
(4)
-(x4)3
应用新知?
应用新知?
注意:运用幂的乘方法则,运算时要先确定符号
八年级
数学
应用新知?
幂的乘方的逆运算:
(1)x13·x7=x(
)=(
)5=(
)4=(
)10;
(2)a2m
=(
)2
=(
)m
(m为正整数).
20
x4
x5
x2
am
a2
幂的乘方法则的逆用
应用新知?
(1)、若
am
=
2,
则a3m
=_____.
动脑筋!
应用新知
(2)
、若
mx
=
2,
my
=
3
,
则
mx+y
=__,
m3x+2y
=______.
(4)
、在255,344,433,522这四个幂中,
数值最大的一个是?说明理由.
1、下列各式对吗?请说出你的观点和理由:
(1)
(a4)3=a7
(
)
(2)
a4
a3=a12
(
)
(3)
(a2)3+(a3)2=(a6)2
(
)
×
×
×
?
巩固新知?
2.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1
(B)(xm+1)5
(C)
x
·
(x5)m
(D)
x
·
x5
·
xm
c
3.x14不可以写成( )
(A)x5
·
(x3)3
(B)
(-x)
·
(-x2)
·
(-x3)
·
(-x8)
(C)(x7)7
(D)x3
·
x4
·
x5
·
x2
C
巩固新知?
课堂小结
1.幂的乘方的法则
(m、n都是正整数)
幂的乘方,底数不变,指数相乘.
语言叙述
符号叙述
.
2.幂的乘方的法则可以逆用.即
3.多重乘方也具有这一性质.如
(其中
m、n、p都是正整数).
1.若(9n)2
=
38
,则n为______
课后拓展
2.
设n为正整数,且x2n=2,
求9(x3n)2的值.
3.如果甲球的半径是乙球的n倍,那么甲球的体积是乙球的n3倍.地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
课后拓展
人教版八年级(上册)
3
面积S=
.
面积S=
.
体积V=
.
你能说出各式的底和指数吗?
引入新知?
(32)3=32×32×32=3(
);
(a2)3=a2×a2×a2=a(
).
(am)3=am·am·am=a(
)
(m是正整数)
根据乘方的意义及同底数幂的乘法填空,看
看计算的结果有什么规律:
这几道题有什么共同的特点呢?计算的结果有什么规律吗?
观察:
(2)
(3)
猜想:
探索新知
?
(a2)3=
a6
(1)
探索新知
?
幂的乘方,
(am)n
=
amn
幂的乘方
底数不变,指数相乘
(m,n都是正整数
)
底数不变,指数相乘.
幂的乘方法则:
归纳结论?
乘法
乘方
不变
不变
指数
相加
指数
相乘
区别旧知
运算
种类
公式
法则
中运算
计算结果
底数
指数
同底数幂乘法
幂的乘方
(1)
(103)5
(2)
(a4)4
(3)
(am)2
(4)
-(x4)3
应用新知?
应用新知?
注意:运用幂的乘方法则,运算时要先确定符号
八年级
数学
应用新知?
幂的乘方的逆运算:
(1)x13·x7=x(
)=(
)5=(
)4=(
)10;
(2)a2m
=(
)2
=(
)m
(m为正整数).
20
x4
x5
x2
am
a2
幂的乘方法则的逆用
应用新知?
(1)、若
am
=
2,
则a3m
=_____.
动脑筋!
应用新知
(2)
、若
mx
=
2,
my
=
3
,
则
mx+y
=__,
m3x+2y
=______.
(4)
、在255,344,433,522这四个幂中,
数值最大的一个是?说明理由.
1、下列各式对吗?请说出你的观点和理由:
(1)
(a4)3=a7
(
)
(2)
a4
a3=a12
(
)
(3)
(a2)3+(a3)2=(a6)2
(
)
×
×
×
?
巩固新知?
2.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1
(B)(xm+1)5
(C)
x
·
(x5)m
(D)
x
·
x5
·
xm
c
3.x14不可以写成( )
(A)x5
·
(x3)3
(B)
(-x)
·
(-x2)
·
(-x3)
·
(-x8)
(C)(x7)7
(D)x3
·
x4
·
x5
·
x2
C
巩固新知?
课堂小结
1.幂的乘方的法则
(m、n都是正整数)
幂的乘方,底数不变,指数相乘.
语言叙述
符号叙述
.
2.幂的乘方的法则可以逆用.即
3.多重乘方也具有这一性质.如
(其中
m、n、p都是正整数).
1.若(9n)2
=
38
,则n为______
课后拓展
2.
设n为正整数,且x2n=2,
求9(x3n)2的值.
3.如果甲球的半径是乙球的n倍,那么甲球的体积是乙球的n3倍.地球、木星、太阳可以近似地看做是球体.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
课后拓展
