人教版八年级上册数学第5讲轴对称图形的认识和画法讲义 (含解析)
文档属性
| 名称 | 人教版八年级上册数学第5讲轴对称图形的认识和画法讲义 (含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 13:09:51 | ||
图片预览



文档简介
第5讲
轴对称图形的认识和画法
知识定位
讲解用时:3分钟
A、适用范围:人教版初二,基础一般;
B、知识点概述:本讲义主要用于人教版初二新课,本节课我们要学习轴对称图形,学会区分轴对称图形和轴对称,明确轴对称图形有多少条对称轴,以及判断我们所学的基本图形是否为轴对称图形。
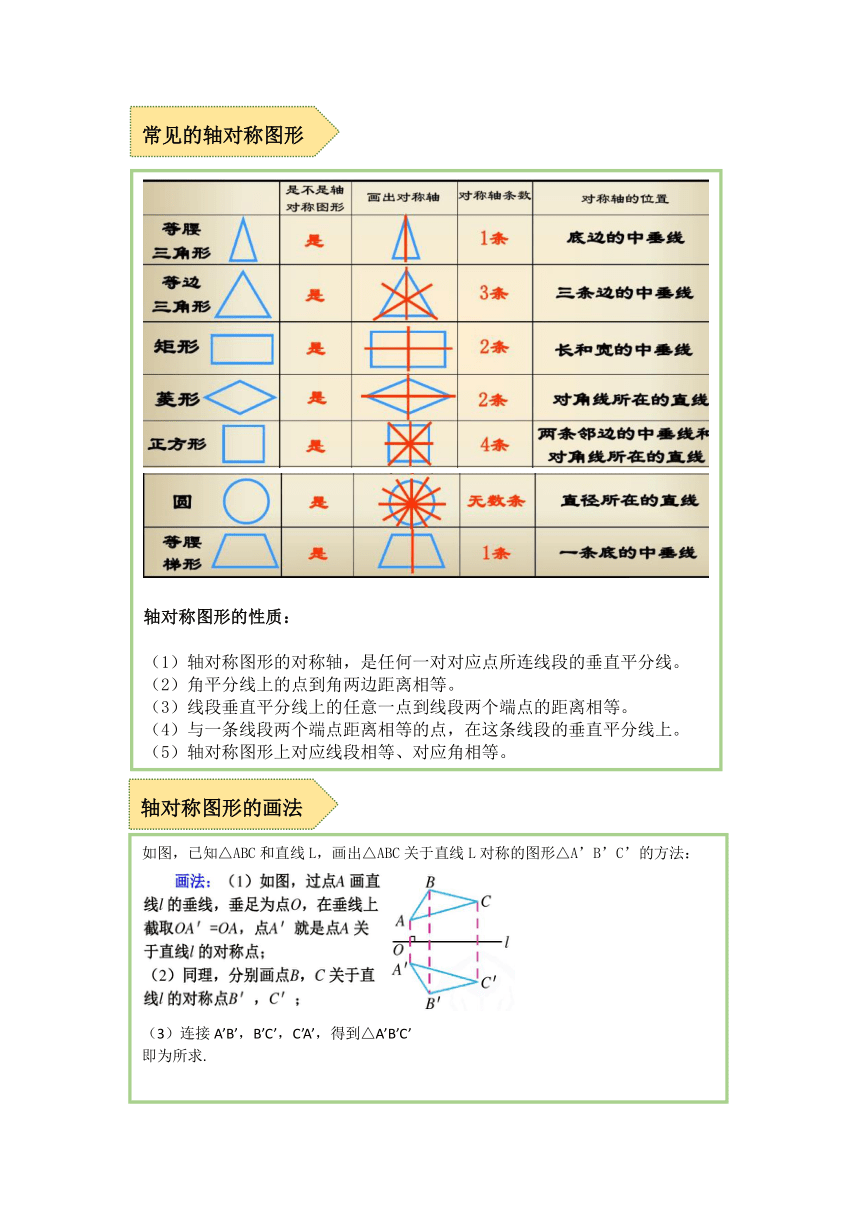
知识梳理
讲解用时:20分钟
线段是轴对称图形,它的对称轴是这条线段的垂直平分线;
角也是轴对称图形,它的对称轴是这个角的角平
分线所在的直线.
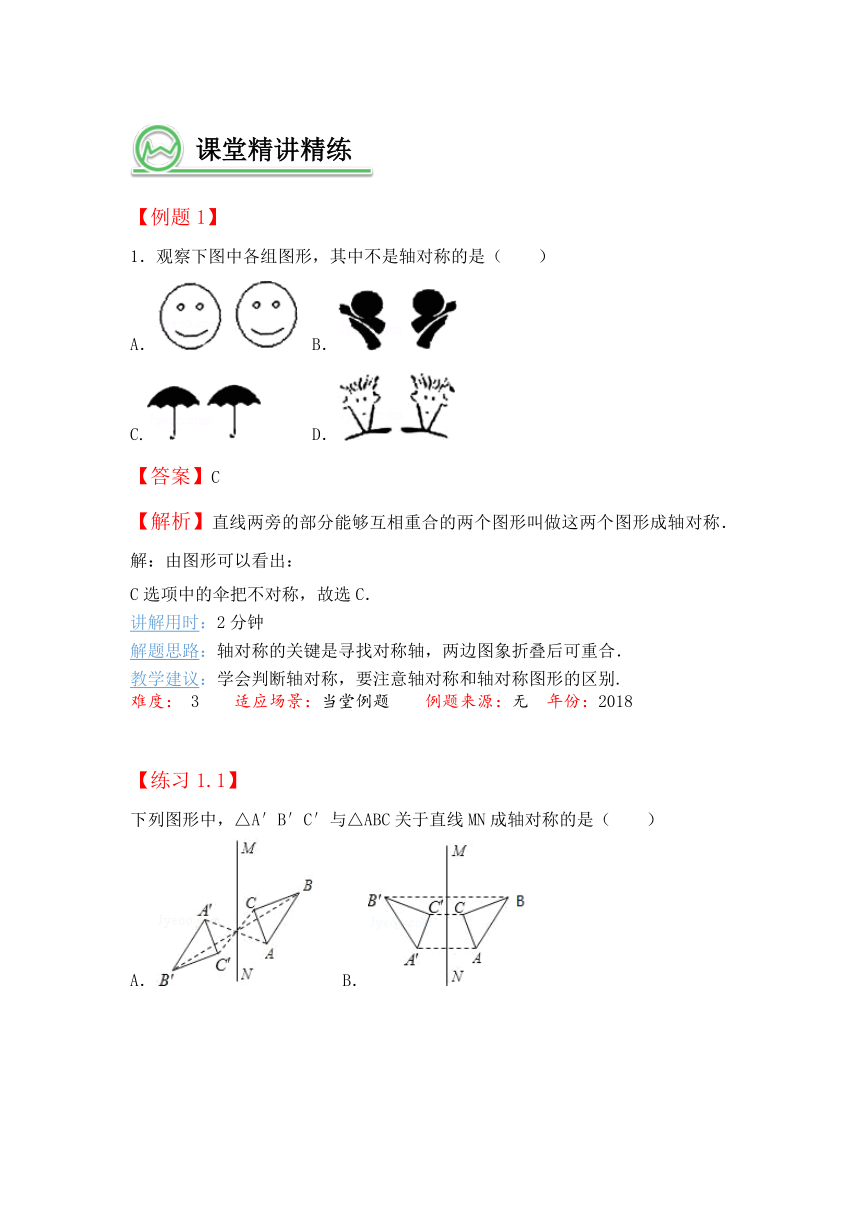
课堂精讲精练
【例题1】
1.观察下图中各组图形,其中不是轴对称的是( )
A.
B.
C.
D.
【答案】C
【解析】直线两旁的部分能够互相重合的两个图形叫做这两个图形成轴对称.
解:由图形可以看出:
C选项中的伞把不对称,故选C.
讲解用时:2分钟
解题思路:轴对称的关键是寻找对称轴,两边图象折叠后可重合.
教学建议:学会判断轴对称,要注意轴对称和轴对称图形的区别.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习1.1】
下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
B.
C.
D.
【答案】B
【解析】认真观察各选项给出的图形,根据轴对称的性质,对称轴垂直平分线对应点的连线进行判断.
解:根据轴对称的性质,结合四个选项,只有B选项中对应点的连线被对称轴MN垂直平分,所以B是符合要求的.
故选:B.
讲解用时:2分钟
解题思路:本题考查轴对称的性质;应用对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分解题是正确解答本题的关键.
教学建议:学会判断轴对称,要注意轴对称和轴对称图形的区别.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题2】
如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为多少?
【答案】60°
【解析】要使白球反弹后能将黑球直接撞入袋中,则∠2=60°,根据∠1、∠2对称,则能求出∠1的度数.
解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠3=30°,
∴∠2=60°,
∴∠1=60°.
故答案为:60°.
讲解用时:3分钟
解题思路:本题是考查图形的对称、旋转、分割以及分类的数学思想.
教学建议:学会观察图形并判断轴对称图形.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习2.1】
如图,某英语单词由四个字母组成,且四个字母都关于直线L对称,则这个英语单词的汉语意思是什么?
【答案】书
【解析】根据轴对称图形的性质,组成图形,即可解答.
解:如图,
这个单词所指的物品是书.
故答案为:书.
讲解用时:1分钟
解题思路:本题考查了轴对称图形,解决本题的关键是根据轴对称的性质,作出图形.
教学建议:学会观察图形并判断轴对称图形.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题3】
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1与△A2B2C2.
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2;
(3)观察△A1B1C和△A2B2C2,他们是否关于某直线对称?若是,请用粗线条画出对称轴.
【答案】见解析
【解析】(1)根据网格结构找出点A、B、C关于y轴的对称点A1、B1、C1的位置,然后顺次连接即可.
(2)根据网格结构找出点A、B、C向右平移6个单位的对应点A2、B2、C2的位置,然后顺次连接即可;
(3)根据轴对称图形的性质和顶点坐标,可得其对称轴是l:x=3.
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)如图所示:直线l即为所求.
讲解用时:3分钟
解题思路:本题考查了轴对称图形的性质和作图﹣平移变换,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
教学建议:学会画轴对称图形.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习3.1】
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)将△ABC向右平移5个单位再向下平移2个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于x轴对称的△A2B2C2;
(3)P(a,b)是△ABC的AC边上的一点,请直接写出经过两次变换后在△A2B2C2中对应的点P2的坐标.
【答案】见解析
【解析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用关于x轴对称点的性质得出对应点位置进而得出答案;
(3)利用平移的性质以及关于x轴对称点的性质得出对应点坐标.
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)∵P(a,b)是△ABC的AC边上的一点,
∴将△ABC向右平移5个单位再向下平移2个单位后得到对应的点的坐标为:(a+5,b﹣2),
∴(a+5,b﹣2)关于x轴对称点的坐标为:(a+5,﹣b+2).
讲解用时:3分钟
解题思路:此题主要考查了轴对称变换以及平移变换,正确得出对应点位置是解题关键.
教学建议:画轴对称图形时,先确定对称点,再把对称点连接即可得到所要求的的图形.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题4】
如图所示,在△ABC中,∠C=90°,AB=16cm,BC的垂直平分线交AB于点D,则点C与点D的距离是
cm.
【答案】8
【解析】首先连接CD,由BC的垂直平分线交AB于点D,根据线段垂直平分线的性质,即可求得CD=BD,又由∠C=90°,根据等角的余角相等,即可求得∠A=∠ACD,则可得AD=CD,继而可求得CD=AB.
解:连接CD,
∵BC的垂直平分线交AB于点D,
∴CD=BD,
∴∠DCB=∠B,
∵∠C=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∴∠A=∠ACD,
∴AD=CD,
∴CD=AD=BD=AB=×16=8(cm).
故答案为:8.
讲解用时:3分钟
解题思路:此题考查了线段垂直平分线的性质、等腰三角形的判定与性质以及直角三角形的性质.此题难度不大,解题的关键是准确作出辅助线,证得CD=AD=BD.
教学建议:熟练掌握垂直平分线的性质并熟练运用.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习4.1】
如图,在△ABC中,AB=AC=3cm,AB的垂直平分线交AC于点N,△BCN的周长是5cm,则BC的长等于
cm.
【答案】2
【解析】由AB的垂直平分线交AC于点N,根据线段的垂直平分线的性质得到NA=NB,而BC+BN+NC=5cm,则BC+AN+NC=5cm,由AC=AN+NC=3cm,即可得到BC的长.
解:∵AB的垂直平分线交AC于点N,
∴NA=NB,
又∵△BCN的周长是5cm,
∴BC+BN+NC=5cm,
∴BC+AN+NC=5cm,
而AC=AN+NC=3cm,
∴BC=2cm.
故答案为:2.
讲解用时:3分钟
解题思路:本题考查了线段的垂直平分线的性质:线段的垂直平分线的点到线段两端点的距离相等;也考查了三角形周长的定义.
教学建议:熟练掌握垂直平分线的性质并熟练运用.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题5】
如图,点P关于OA、OB的对称轴分别为C、D,连结CD,交OA于M,交OB于N.
(1)若CD的长为18厘米,求△PMN的周长;
(2)若∠AOB=48°,求∠MPN.
【答案】(1)18cm;(2)84°
【解析】(1)根据对称轴的意义,可以求出PM=CM,ND=NP,CD=18cm,可以求出△PMN的周长.
(2)要求∠MPN的度数,要在△MPN中进行,根据轴对称的性质和等腰三角形的性质找出与∠CPD的关系,利用已知∠AOB=48°可求出∠CPD,答案可得.
解:(1)∵点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,
∴PM=CM,ND=NP,
∵△PMN的周长=PN+PM+MN,PN+PM+MN=CD=18cm,
∴△PMN的周长=18cm;
(2)PC交OA于R,PD交OB于T
∵P关于OA、OB的对称点是点C、D
∴OA垂直平分PC,OB垂直平分PD
∴CM=PM,PN=DN
∴∠PMN=2∠C,∠PNM=2∠D,
∵∠PRM=∠PTN=90°,
∴在四边形OTPR中,
∴∠CPD+∠O=180°,
∴∠CPD=180°﹣48°=132°
∴∠C+∠D=48°
∴∠MPN=180°﹣48°×2=84°.
讲解用时:3分钟
解题思路:本题考查轴对称的性质与运用,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
教学建议:熟练掌握轴对称的性质和应用,灵活解题.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习5.1】
如图,点P在∠AOB内,点M、N分别是P点关于OA、OB的对称点,且MN交OA、OB相交于点E,若△PEF的周长为20,求MN的长.
【答案】20cm
【解析】根据轴对称的性质可知:EP=EM,PF=FN,所以线段MN的长=△PEF的周长,再根据△PEF的周长为20,即可得出MN的长.
解:∵点M是P点关于OA的对称点,
∴EP=EM,
∵N是P点关于OB的对称点,
∴PF=FN,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长为20,
∴MN=20cm.
讲解用时:3分钟
解题思路:此题主要考查了轴对称的性质:对称轴上的任何一点到两个对应点之间的距离相等.
教学建议:熟练掌握轴对称的性质和应用,灵活解题.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题6】
如图,在△ABC中,AB=AC,DE是AB的中垂线,△BCE的周长为14,BC=6,则AB的长为
.
【答案】8
【解析】由已知条件,利用线段的垂直平分线和已给的周长的值即可求出.
解:∵DE是AB的中垂线
∴AE=BE,
∵△BCE的周长为14
∴BC+CE+BE=BC+CE+AE=BC+AC=14
∵BC=6
∴AC=8
∴AB=AC=8.
故填8.
讲解用时:3分钟
解题思路:本题考查了线段垂直平分线的性质;解决本题的关键是利用线段的垂直平分线性质得到相应线段相等并进行等量代换.
教学建议:熟练掌握垂直平分线的性质并熟练运用.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习6.1】
已知:如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC,AB于点M,N,求证:CM=2BM.
【答案】CM=2BM
【解析】先根据垂直平分线的性质,判定AM=BM,再求出∠B=30°,∠CAM=90°,根据直角三角形中30度的角对的直角边是斜边的一半,得出BM=AM=CA即CM=2BM.
证法1:如答图所示,连接AM,
∵∠BAC=120°,AB=AC,
∴∠B=∠C=30°,
∵MN是AB的垂直平分线,
∴BM=AM,∴∠BAM=∠B=30°,
∴∠MAC=90°,
∴CM=2AM,
∴CM=2BM.
证法二:如答图所示,过A
作AD∥MN交BC于点D.
∵MN是AB的垂直平分线,
∴N是AB的中点.
∵AD∥MN,
∴M是BD的中点,即BM=MD.
∵AC=AB,∠BAC=120°,
∴∠B=∠C=30°,
∵∠BAD=∠BNM=90°,
∴AD=BD=BM=MD,
又∵∠CAD=∠BAC﹣∠BAD=120°﹣90°=30°,
∴∠CAD=∠C,
∴AD=DC,BM=MD=DC,
∴CM=2BM.
讲解用时:4分钟
解题思路:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.
教学建议:掌握线段垂直平分线的性质.
难度:
4
适应场景:当堂练习
例题来源:无
年份:2018
【例题7】
如图,已知四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.
(1)试写出EF,AD的长度;
(2)求∠G的度数;
(3)连接BF,线段BF与直线MN有什么关系?
【答案】(1)EF=3cm,AD=4cm;(2)80°;(3)直线MN垂直平分BF
【解析】(1)根据图形写出对应线段即可;
(2)对称图形的对应角相等,据此求解;
(3)根据“对应点的连线被对称轴垂直平分”求解;
解:(1)∵四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.
∴EF=AB=3cm,AD=EH=4cm;
(2)∵∠B=125°,∠A+∠D=155°,
∴∠C=80°,
∴∠G=∠C=80°;
(3)∵对称轴垂直平分对称点的连线,
∴直线MN垂直平分BF.
讲解用时:4分钟
解题思路:本题考查了轴对称的性质,解题的关键是了解轴对称的性质,难度不大,属于基础题.
教学建议:熟练掌握轴对称的性质与运用.
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【练习7.1】
如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
【答案】∠ABC∠C=60°;∠C=30°
【解析】借助轴对称的性质,A点和E点关于BD对称,有∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD,B点、C点关于DE对称,可得∠DBE=∠BCD,结合上式可得:∠ABC=2∠BCD,且∠ABC+∠BCD=90°,进而求得∠ABC、∠C的值.
解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°
∴∠ABC=2∠C=60°.
讲解用时:3分钟
解题思路:本题考查轴对称的性质与运用.对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
教学建议:熟练掌握轴对称的性质与运用.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
课后作业
【作业1】
下列图案是轴对称图形的有( )个.
A.1
B.2
C.3
D.4
【答案】B
【解析】根据轴对称图形的概念对个图形分析判断即可得解.
解:第一个图形是轴对称图形,
第二个图形不是轴对称图形,
第三个图形不是轴对称图形,
第四个图形是轴对称图形,
综上所述,轴对称图形共有2个.
故选:B.
讲解用时:3分钟
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【作业2】
如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角.
【答案】相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC.
【解析】根据轴对称的性质:把图形沿AF对折,凡是重合的线段都相等,重合的角也都相等.
解:相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC.
讲解用时:3分钟
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【作业3】
如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,求△ABD的周长.
【答案】13
【解析】根据垂直平分线的性质计算.
△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC
解:∵AC的垂直平分线DE交BC于D,E为垂足
∴AD=DC,AC=2AE=6cm,
∵△ABC的周长为19cm,
∴AB+BC=13cm
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm.
故填13.
讲解用时:3分钟
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【作业4】
在平面直角坐标系中按下列要求作图.
(1)作出三象限中的小鱼关于x轴的对称图形;
(2)将(1)中得到的图形再向右平移6个单位长度.
【答案】见解析
【解析】(1)利用轴对称性质,作出小鱼中各顶点关于x轴的对称点,顺次连接,即得到关于x轴对称的图形;
(2)将小鱼的顶点按平移条件找出它的对应点,顺次连接,即得到平移后的图形;
解:如图所示:
讲解用时:3分钟
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【作业5】
如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,MN分
别交OA、OB于E、F.
(1)若△PEF的周长是10cm,求MN的长.
(2)若∠AOB=30°,试求∠MON的度数.
【答案】(1)10cm;(2)60°
【解析】(1)根据轴对称的性质可得ME=PE,NF=PF,然后求出MN=△PEF的周长;
(2)结合线段垂直平分线的性质和等腰三角形的性质推知OP=OM,∠MOA=∠AOP,同理,∠BOP=∠BON,则∠MON=2∠AOB=60°.
解:(1)∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于10cm,
∴MN=10cm;
(2)如图,连接OP、OM、ON.
∵OA垂直平分MP,
∴OP=OM,
∴∠MOA=∠AOP,
同理,∠BOP=∠BON,
∵∠AOB=∠AOP+∠BOP=30°.
∴∠MON=2∠AOB=60°.
讲解用时:3分钟
难度:
4
适应场景:练习题
例题来源:无
年份:2018
轴对称图形的认识和画法
知识定位
讲解用时:3分钟
A、适用范围:人教版初二,基础一般;
B、知识点概述:本讲义主要用于人教版初二新课,本节课我们要学习轴对称图形,学会区分轴对称图形和轴对称,明确轴对称图形有多少条对称轴,以及判断我们所学的基本图形是否为轴对称图形。
知识梳理
讲解用时:20分钟
线段是轴对称图形,它的对称轴是这条线段的垂直平分线;
角也是轴对称图形,它的对称轴是这个角的角平
分线所在的直线.
课堂精讲精练
【例题1】
1.观察下图中各组图形,其中不是轴对称的是( )
A.
B.
C.
D.
【答案】C
【解析】直线两旁的部分能够互相重合的两个图形叫做这两个图形成轴对称.
解:由图形可以看出:
C选项中的伞把不对称,故选C.
讲解用时:2分钟
解题思路:轴对称的关键是寻找对称轴,两边图象折叠后可重合.
教学建议:学会判断轴对称,要注意轴对称和轴对称图形的区别.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习1.1】
下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
B.
C.
D.
【答案】B
【解析】认真观察各选项给出的图形,根据轴对称的性质,对称轴垂直平分线对应点的连线进行判断.
解:根据轴对称的性质,结合四个选项,只有B选项中对应点的连线被对称轴MN垂直平分,所以B是符合要求的.
故选:B.
讲解用时:2分钟
解题思路:本题考查轴对称的性质;应用对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分解题是正确解答本题的关键.
教学建议:学会判断轴对称,要注意轴对称和轴对称图形的区别.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题2】
如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为多少?
【答案】60°
【解析】要使白球反弹后能将黑球直接撞入袋中,则∠2=60°,根据∠1、∠2对称,则能求出∠1的度数.
解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∵∠3=30°,
∴∠2=60°,
∴∠1=60°.
故答案为:60°.
讲解用时:3分钟
解题思路:本题是考查图形的对称、旋转、分割以及分类的数学思想.
教学建议:学会观察图形并判断轴对称图形.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习2.1】
如图,某英语单词由四个字母组成,且四个字母都关于直线L对称,则这个英语单词的汉语意思是什么?
【答案】书
【解析】根据轴对称图形的性质,组成图形,即可解答.
解:如图,
这个单词所指的物品是书.
故答案为:书.
讲解用时:1分钟
解题思路:本题考查了轴对称图形,解决本题的关键是根据轴对称的性质,作出图形.
教学建议:学会观察图形并判断轴对称图形.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题3】
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1与△A2B2C2.
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2;
(3)观察△A1B1C和△A2B2C2,他们是否关于某直线对称?若是,请用粗线条画出对称轴.
【答案】见解析
【解析】(1)根据网格结构找出点A、B、C关于y轴的对称点A1、B1、C1的位置,然后顺次连接即可.
(2)根据网格结构找出点A、B、C向右平移6个单位的对应点A2、B2、C2的位置,然后顺次连接即可;
(3)根据轴对称图形的性质和顶点坐标,可得其对称轴是l:x=3.
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)如图所示:直线l即为所求.
讲解用时:3分钟
解题思路:本题考查了轴对称图形的性质和作图﹣平移变换,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
教学建议:学会画轴对称图形.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习3.1】
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)将△ABC向右平移5个单位再向下平移2个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于x轴对称的△A2B2C2;
(3)P(a,b)是△ABC的AC边上的一点,请直接写出经过两次变换后在△A2B2C2中对应的点P2的坐标.
【答案】见解析
【解析】(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用关于x轴对称点的性质得出对应点位置进而得出答案;
(3)利用平移的性质以及关于x轴对称点的性质得出对应点坐标.
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)∵P(a,b)是△ABC的AC边上的一点,
∴将△ABC向右平移5个单位再向下平移2个单位后得到对应的点的坐标为:(a+5,b﹣2),
∴(a+5,b﹣2)关于x轴对称点的坐标为:(a+5,﹣b+2).
讲解用时:3分钟
解题思路:此题主要考查了轴对称变换以及平移变换,正确得出对应点位置是解题关键.
教学建议:画轴对称图形时,先确定对称点,再把对称点连接即可得到所要求的的图形.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题4】
如图所示,在△ABC中,∠C=90°,AB=16cm,BC的垂直平分线交AB于点D,则点C与点D的距离是
cm.
【答案】8
【解析】首先连接CD,由BC的垂直平分线交AB于点D,根据线段垂直平分线的性质,即可求得CD=BD,又由∠C=90°,根据等角的余角相等,即可求得∠A=∠ACD,则可得AD=CD,继而可求得CD=AB.
解:连接CD,
∵BC的垂直平分线交AB于点D,
∴CD=BD,
∴∠DCB=∠B,
∵∠C=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∴∠A=∠ACD,
∴AD=CD,
∴CD=AD=BD=AB=×16=8(cm).
故答案为:8.
讲解用时:3分钟
解题思路:此题考查了线段垂直平分线的性质、等腰三角形的判定与性质以及直角三角形的性质.此题难度不大,解题的关键是准确作出辅助线,证得CD=AD=BD.
教学建议:熟练掌握垂直平分线的性质并熟练运用.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习4.1】
如图,在△ABC中,AB=AC=3cm,AB的垂直平分线交AC于点N,△BCN的周长是5cm,则BC的长等于
cm.
【答案】2
【解析】由AB的垂直平分线交AC于点N,根据线段的垂直平分线的性质得到NA=NB,而BC+BN+NC=5cm,则BC+AN+NC=5cm,由AC=AN+NC=3cm,即可得到BC的长.
解:∵AB的垂直平分线交AC于点N,
∴NA=NB,
又∵△BCN的周长是5cm,
∴BC+BN+NC=5cm,
∴BC+AN+NC=5cm,
而AC=AN+NC=3cm,
∴BC=2cm.
故答案为:2.
讲解用时:3分钟
解题思路:本题考查了线段的垂直平分线的性质:线段的垂直平分线的点到线段两端点的距离相等;也考查了三角形周长的定义.
教学建议:熟练掌握垂直平分线的性质并熟练运用.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题5】
如图,点P关于OA、OB的对称轴分别为C、D,连结CD,交OA于M,交OB于N.
(1)若CD的长为18厘米,求△PMN的周长;
(2)若∠AOB=48°,求∠MPN.
【答案】(1)18cm;(2)84°
【解析】(1)根据对称轴的意义,可以求出PM=CM,ND=NP,CD=18cm,可以求出△PMN的周长.
(2)要求∠MPN的度数,要在△MPN中进行,根据轴对称的性质和等腰三角形的性质找出与∠CPD的关系,利用已知∠AOB=48°可求出∠CPD,答案可得.
解:(1)∵点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,
∴PM=CM,ND=NP,
∵△PMN的周长=PN+PM+MN,PN+PM+MN=CD=18cm,
∴△PMN的周长=18cm;
(2)PC交OA于R,PD交OB于T
∵P关于OA、OB的对称点是点C、D
∴OA垂直平分PC,OB垂直平分PD
∴CM=PM,PN=DN
∴∠PMN=2∠C,∠PNM=2∠D,
∵∠PRM=∠PTN=90°,
∴在四边形OTPR中,
∴∠CPD+∠O=180°,
∴∠CPD=180°﹣48°=132°
∴∠C+∠D=48°
∴∠MPN=180°﹣48°×2=84°.
讲解用时:3分钟
解题思路:本题考查轴对称的性质与运用,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
教学建议:熟练掌握轴对称的性质和应用,灵活解题.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习5.1】
如图,点P在∠AOB内,点M、N分别是P点关于OA、OB的对称点,且MN交OA、OB相交于点E,若△PEF的周长为20,求MN的长.
【答案】20cm
【解析】根据轴对称的性质可知:EP=EM,PF=FN,所以线段MN的长=△PEF的周长,再根据△PEF的周长为20,即可得出MN的长.
解:∵点M是P点关于OA的对称点,
∴EP=EM,
∵N是P点关于OB的对称点,
∴PF=FN,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长为20,
∴MN=20cm.
讲解用时:3分钟
解题思路:此题主要考查了轴对称的性质:对称轴上的任何一点到两个对应点之间的距离相等.
教学建议:熟练掌握轴对称的性质和应用,灵活解题.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
【例题6】
如图,在△ABC中,AB=AC,DE是AB的中垂线,△BCE的周长为14,BC=6,则AB的长为
.
【答案】8
【解析】由已知条件,利用线段的垂直平分线和已给的周长的值即可求出.
解:∵DE是AB的中垂线
∴AE=BE,
∵△BCE的周长为14
∴BC+CE+BE=BC+CE+AE=BC+AC=14
∵BC=6
∴AC=8
∴AB=AC=8.
故填8.
讲解用时:3分钟
解题思路:本题考查了线段垂直平分线的性质;解决本题的关键是利用线段的垂直平分线性质得到相应线段相等并进行等量代换.
教学建议:熟练掌握垂直平分线的性质并熟练运用.
难度:
3
适应场景:当堂例题
例题来源:无
年份:2018
【练习6.1】
已知:如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC,AB于点M,N,求证:CM=2BM.
【答案】CM=2BM
【解析】先根据垂直平分线的性质,判定AM=BM,再求出∠B=30°,∠CAM=90°,根据直角三角形中30度的角对的直角边是斜边的一半,得出BM=AM=CA即CM=2BM.
证法1:如答图所示,连接AM,
∵∠BAC=120°,AB=AC,
∴∠B=∠C=30°,
∵MN是AB的垂直平分线,
∴BM=AM,∴∠BAM=∠B=30°,
∴∠MAC=90°,
∴CM=2AM,
∴CM=2BM.
证法二:如答图所示,过A
作AD∥MN交BC于点D.
∵MN是AB的垂直平分线,
∴N是AB的中点.
∵AD∥MN,
∴M是BD的中点,即BM=MD.
∵AC=AB,∠BAC=120°,
∴∠B=∠C=30°,
∵∠BAD=∠BNM=90°,
∴AD=BD=BM=MD,
又∵∠CAD=∠BAC﹣∠BAD=120°﹣90°=30°,
∴∠CAD=∠C,
∴AD=DC,BM=MD=DC,
∴CM=2BM.
讲解用时:4分钟
解题思路:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.
教学建议:掌握线段垂直平分线的性质.
难度:
4
适应场景:当堂练习
例题来源:无
年份:2018
【例题7】
如图,已知四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.
(1)试写出EF,AD的长度;
(2)求∠G的度数;
(3)连接BF,线段BF与直线MN有什么关系?
【答案】(1)EF=3cm,AD=4cm;(2)80°;(3)直线MN垂直平分BF
【解析】(1)根据图形写出对应线段即可;
(2)对称图形的对应角相等,据此求解;
(3)根据“对应点的连线被对称轴垂直平分”求解;
解:(1)∵四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.
∴EF=AB=3cm,AD=EH=4cm;
(2)∵∠B=125°,∠A+∠D=155°,
∴∠C=80°,
∴∠G=∠C=80°;
(3)∵对称轴垂直平分对称点的连线,
∴直线MN垂直平分BF.
讲解用时:4分钟
解题思路:本题考查了轴对称的性质,解题的关键是了解轴对称的性质,难度不大,属于基础题.
教学建议:熟练掌握轴对称的性质与运用.
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【练习7.1】
如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
【答案】∠ABC∠C=60°;∠C=30°
【解析】借助轴对称的性质,A点和E点关于BD对称,有∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD,B点、C点关于DE对称,可得∠DBE=∠BCD,结合上式可得:∠ABC=2∠BCD,且∠ABC+∠BCD=90°,进而求得∠ABC、∠C的值.
解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°
∴∠ABC=2∠C=60°.
讲解用时:3分钟
解题思路:本题考查轴对称的性质与运用.对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
教学建议:熟练掌握轴对称的性质与运用.
难度:
3
适应场景:当堂练习
例题来源:无
年份:2018
课后作业
【作业1】
下列图案是轴对称图形的有( )个.
A.1
B.2
C.3
D.4
【答案】B
【解析】根据轴对称图形的概念对个图形分析判断即可得解.
解:第一个图形是轴对称图形,
第二个图形不是轴对称图形,
第三个图形不是轴对称图形,
第四个图形是轴对称图形,
综上所述,轴对称图形共有2个.
故选:B.
讲解用时:3分钟
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【作业2】
如图,五边形ABCDE是轴对称图形,线段AF所在直线为对称轴,找出图中所有相等的线段和相等的角.
【答案】相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC.
【解析】根据轴对称的性质:把图形沿AF对折,凡是重合的线段都相等,重合的角也都相等.
解:相等的线段:AB=AE,CB=DE,CF=DF;
相等的角:∠B=∠E,∠C=∠D,∠BAF=∠EAF,∠AFD=∠AFC.
讲解用时:3分钟
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【作业3】
如图,△ABC的周长为19cm,AC的垂直平分线DE交BC于D,E为垂足,AE=3cm,求△ABD的周长.
【答案】13
【解析】根据垂直平分线的性质计算.
△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC
解:∵AC的垂直平分线DE交BC于D,E为垂足
∴AD=DC,AC=2AE=6cm,
∵△ABC的周长为19cm,
∴AB+BC=13cm
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm.
故填13.
讲解用时:3分钟
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【作业4】
在平面直角坐标系中按下列要求作图.
(1)作出三象限中的小鱼关于x轴的对称图形;
(2)将(1)中得到的图形再向右平移6个单位长度.
【答案】见解析
【解析】(1)利用轴对称性质,作出小鱼中各顶点关于x轴的对称点,顺次连接,即得到关于x轴对称的图形;
(2)将小鱼的顶点按平移条件找出它的对应点,顺次连接,即得到平移后的图形;
解:如图所示:
讲解用时:3分钟
难度:
3
适应场景:练习题
例题来源:无
年份:2018
【作业5】
如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,MN分
别交OA、OB于E、F.
(1)若△PEF的周长是10cm,求MN的长.
(2)若∠AOB=30°,试求∠MON的度数.
【答案】(1)10cm;(2)60°
【解析】(1)根据轴对称的性质可得ME=PE,NF=PF,然后求出MN=△PEF的周长;
(2)结合线段垂直平分线的性质和等腰三角形的性质推知OP=OM,∠MOA=∠AOP,同理,∠BOP=∠BON,则∠MON=2∠AOB=60°.
解:(1)∵M、N分别是点P关于AO、BO的对称点,
∴ME=PE,NF=PF,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∵△PEF的周长等于10cm,
∴MN=10cm;
(2)如图,连接OP、OM、ON.
∵OA垂直平分MP,
∴OP=OM,
∴∠MOA=∠AOP,
同理,∠BOP=∠BON,
∵∠AOB=∠AOP+∠BOP=30°.
∴∠MON=2∠AOB=60°.
讲解用时:3分钟
难度:
4
适应场景:练习题
例题来源:无
年份:2018
