冀教版八年级数学上册17.4 直角三角形全等的判定课件(共28张PPT)
文档属性
| 名称 | 冀教版八年级数学上册17.4 直角三角形全等的判定课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 995.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 11:11:46 | ||
图片预览







文档简介
(共28张PPT)
第十七章
特殊三角形
17.4
直角三角形全等的判定
1
直角三角形的全等的判定方法
2
直角三角形全等判定的运用
CONTENTS
1
新知导入
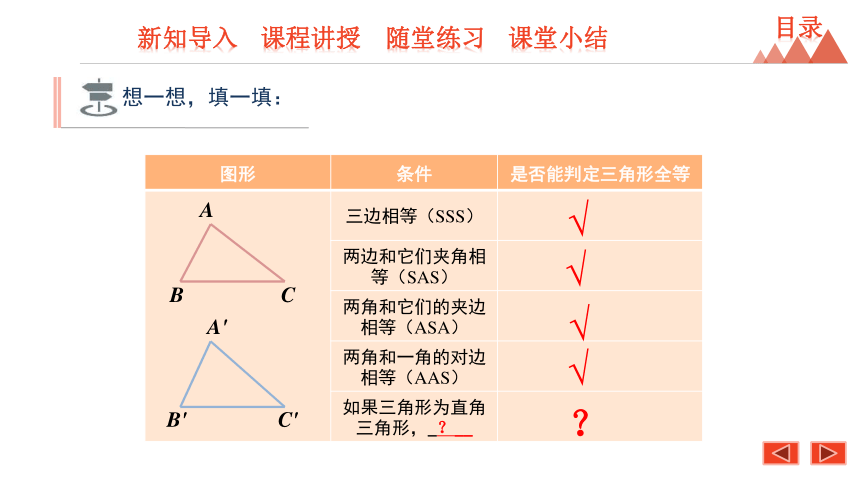
想一想,填一填:
图形
条件
是否能判定三角形全等
三边相等(SSS)
两边和它们夹角相等(SAS)
两角和它们的夹边相等(ASA)
两角和一角的对边相等(AAS)
如果三角形为直角三角形,_?__
A
B
C
A'
B'
C'
√
√
?
√
√
CONTENTS
2
课程讲授
利用“HL”判定直角三角形全等
问题1.1
两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,AAS
利用“HL”判定直角三角形全等
问题1.2
两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,ASA
利用“HL”判定直角三角形全等
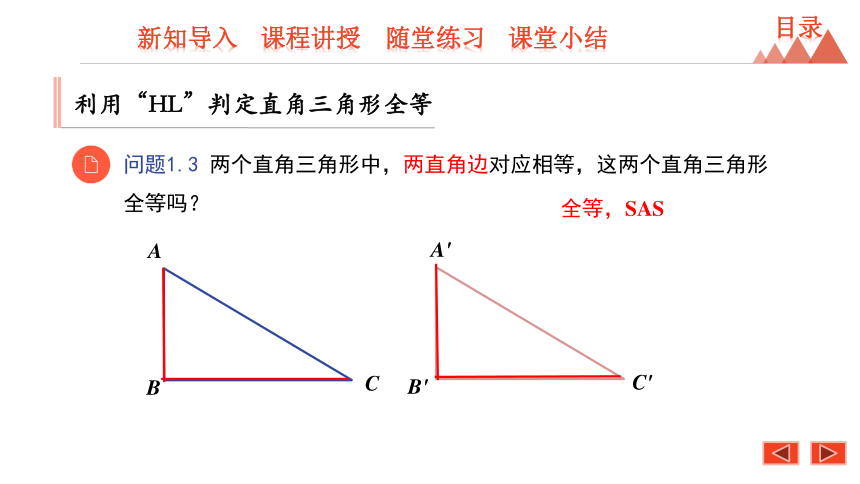
问题1.3
两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,SAS
利用“HL”判定直角三角形全等
问题1.4
两个直角三角形中,两边对应相等,这两个直角三角形全等吗?
如何证明?
A
B
C
A'
B'
C'
已知:如图,在△ABC和△A′B′C′中,
∠C=∠
C′=90°,AB
=
A′B′
,AC=
A′C′.?
?
求证:△ABC≌△A′B′C′.
利用“HL”判定直角三角形全等
A
B
C
A'
B'
C'
证明:在△ABC和△A′B′C′中,
∵∠C=90°,∠C′=90°,
∴BC2=AB2-AC2,
B′C′2=A′B′2-A′C′2(勾股定理).
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
利用“HL”判定直角三角形全等
归纳:直角三角形全等的判定定理:
_____和________对应相等的两个直角三角形全等.(可简写成“_____________”或“_____”)
几何语言:
在Rt△ABC和Rt△A'B'C'中,
BC
=____,
AB
=
_____,
∴Rt△ABC
≌Rt△A'B'C'(____).
直角边
斜边
B'C'
A'B'
斜边、直角边
HL
HL
A
B
C
A'
B'
C'
利用“HL”判定直角三角形全等
例1
已知一直角边和斜边,用尺规作直角三角形.
已知:如图,线段a,c.
求作:△ABC,使∠C=90°,BC=a,AB=c.
a
c
利用“HL”判定直角三角形全等
作法:
(1)作线段CB=a,
(2)过点C,作MC⊥CB.
(3)以B为圆心,c为半径画弧,交CM于点A,
(4)连接AB.
C
M
B
A
利用“HL”判定直角三角形全等
例2
已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB,垂足分别为C,
D,且PC=PD.
求证:点P在∠AOB的平分线上.
A
B
C
D
O
P
利用“HL”判定直角三角形全等
证明:如图,作射线OP.
∵PC⊥OA,
PD⊥OB,∴∠PCO=∠PDO=90°.
在
Rt△OPC
和
Rt△OPD
中,
∴Rt△OFC≌Rt△OPD(
HL).
∴∠POA=∠POB.∴OP是∠AOB的平分线,
即点P在∠AOB的平分线上.
A
B
C
D
O
P
利用“HL”判定直角三角形全等
练一练:如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,以下给出的条件适合的是(
)
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
直角三角形全等判定的运用
例
如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=
AF,AC=AE.
求证:BC=BE.
E
D
A
C
B
F
提示:证明两个直角三角形全等,就可以得出线段的等量关系.
?
直角三角形全等判定的运用
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
E
D
A
C
B
F
直角三角形全等判定的运用
归纳:“HL”是判断两个直角三角形全等的简便方法,对于一般的三角形不成立,在使用时要注意其应用的范围.同时,利用“HL”还能说明两直线的位置关系,在实际解题过程中要结合实际灵活运用.
直角三角形全等判定的运用
练一练:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么下列各条件中,不能使Rt△ABC和Rt△A′B′C′全等的是(
)
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
B
B
A
C
B'
A'
C'
CONTENTS
3
随堂练习
1.下列条件:
①两条直角边对应相等;
②斜边和一锐角对应相等;
③斜边和一直角边对应相等;
④直角边和一锐角对应相等.
以上能判定两直角三角形全等的个数有(
)
A.1个
B.2个
C.3个
D.4个
D
2.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点
E
,AD、CE交于点H,已知EH=EB=3,AE=4,
则
CH的长为(
)
A.1
B.2
C.3
D.4
A
A
B
C
E
D
H
3.如图,在△ABC中,∠C=90°,DE⊥AB于点E,DE=DC,若AC=6,则AD+DE等于(
)
A.7
B.6
C.5
D.4
B
4.如图,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,且OB=OC,有下列结论:
①∠1=∠2;
②△ADO≌△AEO;
③△BOD≌△COE;
④图中有四组三角形全等.
其中正确的个数有______个.
2
5.如图,在△ABC中,已知BD⊥AC,CE
⊥AB,BD=CE.
求证:△EBC≌△DCB.
A
B
C
E
D
证明:
∵
BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90
°.
在
Rt△EBC
和Rt△DCB
中,
CE=BD,
BC=CB
.
∴Rt△EBC≌Rt△DCB
(HL).
CONTENTS
4
课堂小结
“HL”
内容
斜边和一条直角边分别相等的两个直角三角形全等.(简写成“斜边,直角边”或“HL”)
应用
1.使用的前提条件是在直角三角形中
2.遇到直角三角形全等问题,优先考虑“HL”
3.使用时只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
第十七章
特殊三角形
17.4
直角三角形全等的判定
1
直角三角形的全等的判定方法
2
直角三角形全等判定的运用
CONTENTS
1
新知导入
想一想,填一填:
图形
条件
是否能判定三角形全等
三边相等(SSS)
两边和它们夹角相等(SAS)
两角和它们的夹边相等(ASA)
两角和一角的对边相等(AAS)
如果三角形为直角三角形,_?__
A
B
C
A'
B'
C'
√
√
?
√
√
CONTENTS
2
课程讲授
利用“HL”判定直角三角形全等
问题1.1
两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,AAS
利用“HL”判定直角三角形全等
问题1.2
两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,ASA
利用“HL”判定直角三角形全等
问题1.3
两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,SAS
利用“HL”判定直角三角形全等
问题1.4
两个直角三角形中,两边对应相等,这两个直角三角形全等吗?
如何证明?
A
B
C
A'
B'
C'
已知:如图,在△ABC和△A′B′C′中,
∠C=∠
C′=90°,AB
=
A′B′
,AC=
A′C′.?
?
求证:△ABC≌△A′B′C′.
利用“HL”判定直角三角形全等
A
B
C
A'
B'
C'
证明:在△ABC和△A′B′C′中,
∵∠C=90°,∠C′=90°,
∴BC2=AB2-AC2,
B′C′2=A′B′2-A′C′2(勾股定理).
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
利用“HL”判定直角三角形全等
归纳:直角三角形全等的判定定理:
_____和________对应相等的两个直角三角形全等.(可简写成“_____________”或“_____”)
几何语言:
在Rt△ABC和Rt△A'B'C'中,
BC
=____,
AB
=
_____,
∴Rt△ABC
≌Rt△A'B'C'(____).
直角边
斜边
B'C'
A'B'
斜边、直角边
HL
HL
A
B
C
A'
B'
C'
利用“HL”判定直角三角形全等
例1
已知一直角边和斜边,用尺规作直角三角形.
已知:如图,线段a,c.
求作:△ABC,使∠C=90°,BC=a,AB=c.
a
c
利用“HL”判定直角三角形全等
作法:
(1)作线段CB=a,
(2)过点C,作MC⊥CB.
(3)以B为圆心,c为半径画弧,交CM于点A,
(4)连接AB.
C
M
B
A
利用“HL”判定直角三角形全等
例2
已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB,垂足分别为C,
D,且PC=PD.
求证:点P在∠AOB的平分线上.
A
B
C
D
O
P
利用“HL”判定直角三角形全等
证明:如图,作射线OP.
∵PC⊥OA,
PD⊥OB,∴∠PCO=∠PDO=90°.
在
Rt△OPC
和
Rt△OPD
中,
∴Rt△OFC≌Rt△OPD(
HL).
∴∠POA=∠POB.∴OP是∠AOB的平分线,
即点P在∠AOB的平分线上.
A
B
C
D
O
P
利用“HL”判定直角三角形全等
练一练:如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,以下给出的条件适合的是(
)
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
直角三角形全等判定的运用
例
如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=
AF,AC=AE.
求证:BC=BE.
E
D
A
C
B
F
提示:证明两个直角三角形全等,就可以得出线段的等量关系.
?
直角三角形全等判定的运用
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
E
D
A
C
B
F
直角三角形全等判定的运用
归纳:“HL”是判断两个直角三角形全等的简便方法,对于一般的三角形不成立,在使用时要注意其应用的范围.同时,利用“HL”还能说明两直线的位置关系,在实际解题过程中要结合实际灵活运用.
直角三角形全等判定的运用
练一练:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么下列各条件中,不能使Rt△ABC和Rt△A′B′C′全等的是(
)
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
B
B
A
C
B'
A'
C'
CONTENTS
3
随堂练习
1.下列条件:
①两条直角边对应相等;
②斜边和一锐角对应相等;
③斜边和一直角边对应相等;
④直角边和一锐角对应相等.
以上能判定两直角三角形全等的个数有(
)
A.1个
B.2个
C.3个
D.4个
D
2.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点
E
,AD、CE交于点H,已知EH=EB=3,AE=4,
则
CH的长为(
)
A.1
B.2
C.3
D.4
A
A
B
C
E
D
H
3.如图,在△ABC中,∠C=90°,DE⊥AB于点E,DE=DC,若AC=6,则AD+DE等于(
)
A.7
B.6
C.5
D.4
B
4.如图,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,且OB=OC,有下列结论:
①∠1=∠2;
②△ADO≌△AEO;
③△BOD≌△COE;
④图中有四组三角形全等.
其中正确的个数有______个.
2
5.如图,在△ABC中,已知BD⊥AC,CE
⊥AB,BD=CE.
求证:△EBC≌△DCB.
A
B
C
E
D
证明:
∵
BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90
°.
在
Rt△EBC
和Rt△DCB
中,
CE=BD,
BC=CB
.
∴Rt△EBC≌Rt△DCB
(HL).
CONTENTS
4
课堂小结
“HL”
内容
斜边和一条直角边分别相等的两个直角三角形全等.(简写成“斜边,直角边”或“HL”)
应用
1.使用的前提条件是在直角三角形中
2.遇到直角三角形全等问题,优先考虑“HL”
3.使用时只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
