-五年级上数学秋季班课程——第20讲-期末复习(二)(沪教版)有答案
文档属性
| 名称 | -五年级上数学秋季班课程——第20讲-期末复习(二)(沪教版)有答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 241.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 00:00:00 | ||
图片预览




文档简介
学员姓名:
学科教师:
年
级:
辅导科目:
授课日期
时
间
主
题
期末复习(二)
教学内容
1.平行四边形、三角形、梯形及组合图形的面积;
2.期末模拟测试,查漏补缺.
(此环节设计时间在20—25分钟)
易错题整理
判断题(对的在括号内打"√",错的打"×").
(1)两个面积相等的三角形可以拼成一个平行四边形。(
)
(2)两个面积相等的三角形,它们的底和高一定相等。(
)
(3)梯形的面积等于梯形的上底加下底的和乘以高再除以2。(
)
(4)两个面积相等的梯形可以拼成一个平行四边形。(
)
(5)两个同底等高的三角形,形状相同,面积相等。(
)
二、填空题
(1)一个三角形的面积是4.8m2,与它等底等高的平行四边形的面积是(
)
(2)三角形一条边长是4.5分米,这条边上的高是8.6分米;另一条边长是3分米,则这条边上的高是(
).
(3)一个平行四边形,底为8分米,高2分米.如果底不变,高增加2分米,则面积增加(
);底和高都扩大5倍;它的面积扩大(
).
(4)一个梯形的面积是76平方厘米,下底是12厘米,上底是8厘米,梯形的高是(
)厘米。
(5)一个梯形的上底是2厘米,下底是4厘米,高是3厘米,求梯形面积的算式是(
)。当下底缩短到2厘米时,梯形变成(
),这时的面积是(
)平方厘米;当上底等于0时,梯形变成(
),这时的面积是(
)平方厘米。
三、选择题
(1)两个完全一样的三角形,可以拼成一个(
)。
A.长方形
B.正方形
C.梯形
D.平行四边形
(2)一个三角形,它的任意一条边上的高都是它的对称轴,这个三角形是(
)。
A.直角三角形
B.钝角三角形
C.等腰三角形
D.等边三角形
(3)一个直角三角形的两条直角边分别是3厘米和4厘米,斜边是5厘米,那么斜边上的高是(
)。
A.2
厘米
B.2.4厘米
C.3厘米
D.2.5厘米
(4)从平行四边形的一个顶点向对边可以作(
)条高。
A.一
B.两
C.四
D.无数
(
A
B
D
E
F
C
)(5)如图,ABCD是一个直角梯形,AECD是一个平行四边形,DF是梯形的高。两个阴影三角形的面积(
)。
A.=
B.
>
C.
<
D.无法比较
教法指导:先由学生做,同学之间互相批改,错误率高的题目由老师细致讲解,错误率低的题目可以让做对的学生向做错的学生讲解,老师做补充,做得都对的题目可以随机让学生讲解给大家听。
参考答案:
一、(1)×
(2)×
(3)√
(4)×
(5)×
二、(1)9.6m2
(2)12.9分米
(3)16平方分米
25倍
(4)7.6
(5)
平行四边形
6
三角形
6
三、(1)D
(2)C
(3)B
(4)B
(5)A
(此环节设计时间在40—50分钟)
例题1:一块长15米,宽10米的草地外面围一条宽1.5米的小路,求小路的面积?
(
15米
10米
)
教法指导:引导学生将实际问题转化成理论问题,正确求出外围长方形的长和宽,其实是分别加上小路宽的两倍,长是18米,宽是13米。小路的面积等于大长方形的面积减去小长方形的面积。也可以将小路分成四个窄点的长方形来求其面积。
参考答案:小路的面积为18×13-15×10=84(平方米)
试一试:如图,一个三角形的底长5米,如果底延长1米,那么面积就增加1.5平方米。那么原来三角形的面积是多少平方米?
????????
教法指导:通过图形可知延长底边,增加的是个三角形,求出这个三角形的高即求出了原来三角形的高,即可求出原来三角形的面积。这里需要注意,在已知三角形面积和底的前提下求三角形的高,不要先将面积乘以2.
参考答案:1.5×2÷1=3(m),3×5÷2=7.5(m2),即原来三角形的面积为7.5m2
例题2:下图中,三角形BCE的面积是6.3平方厘米,求直角梯形ABCD的面积。
(
A
2.4cm
B
2.8cm
F
C
D
E
3.2cm
)
教法指导:已知梯形的两个底,需要先求出梯形的高BC,在三角形BCE中,已知三角形的面积和高,可以求出底BC,即梯形ABCD的高。
参考答案:6.3×2÷2.8=4.5(cm),(2.4+3.2)×4.5÷2=12.6(cm2),即直角梯形ABCD的面积为12.6平方厘米。
试一试:下图的梯形的面积是9.57平方米,求阴影部分的面积。
教法指导:先由梯形的面积、上底和下底先求出梯形的高,这个高即为阴影部分的三角形以2为底的高。
参考答案:9.57×2÷(2+3.8)=3.3(m),3.3×2÷2=3.3(m2),即阴影部分的面积为3.3m2
例题3:如图,BD、DE、EC的长分别是2厘米,4厘米,2厘米,F是线段AE的中点,三角形ABC以BC为底的高为4厘米,求三角形DEF的面积。
教法指导:联结AD,则三角形ADE以DE为底的高与三角形ABC以BC为底的高相同,都为4厘米,先求出三角形ADE的面积,而三角形ADF和三角形EDF等底同高,故面积相等,所以三角形DEF的面积是三角形ADE面积的一半。
参考答案:三角形ADE的面积为4×4÷2=8(cm2),8÷2=4(cm2),及三角形DEF的面积为4cm2
试一试:已知BD长是2厘米,DC长是3厘米,E是AD的中点,如果三角形ABD的面积是5平方厘米,那么三角形DEC面积是多少?
教法指导:三角形ABD以BD为底和三角形ACD以CD为底同高,可以先求出三角形ACD的面积,再根据三角形ACE和三角形CDE等底同高求出三角形DEC的面积。
参考答案:三角形ACD的面积为5÷2×3=7.5(cm2),三角形CDE的面积为7.5÷2=3.75(cm2)
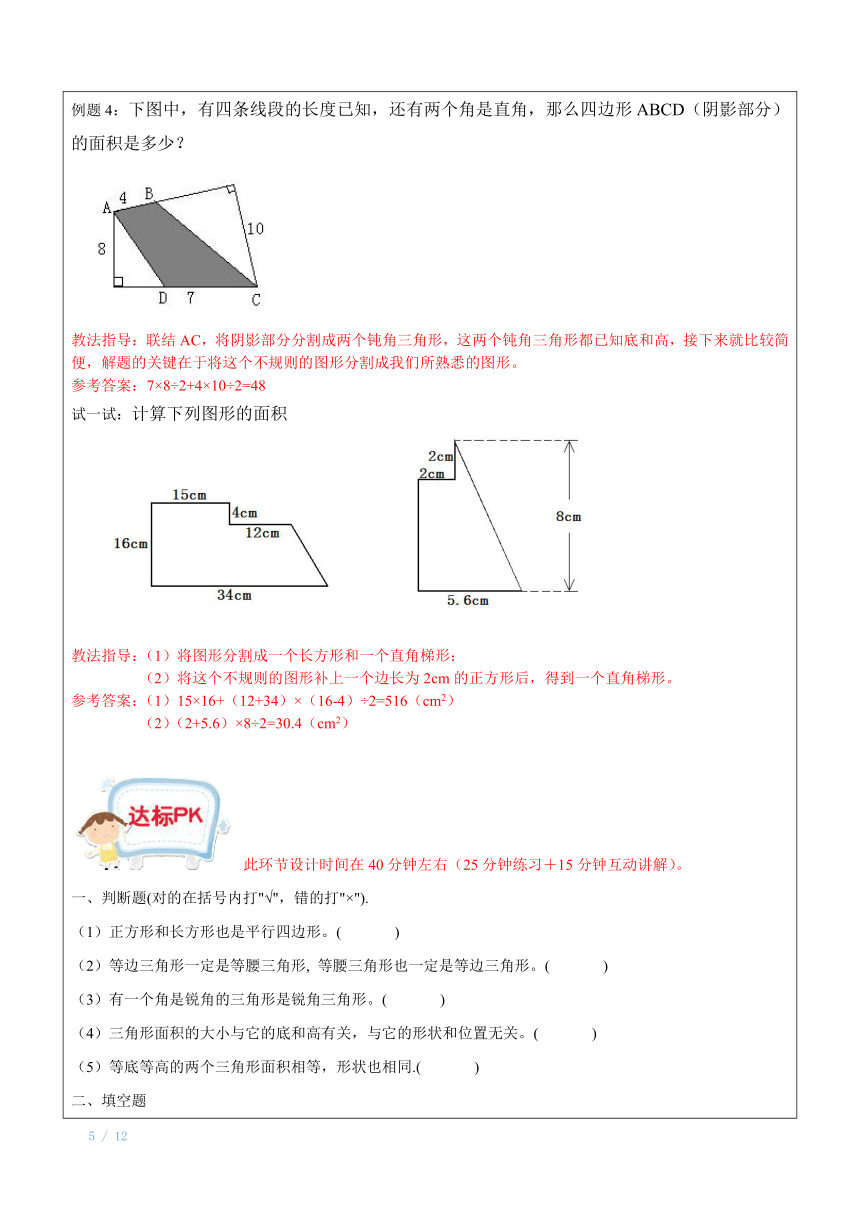
例题4:下图中,有四条线段的长度已知,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?
教法指导:联结AC,将阴影部分分割成两个钝角三角形,这两个钝角三角形都已知底和高,接下来就比较简便,解题的关键在于将这个不规则的图形分割成我们所熟悉的图形。
参考答案:7×8÷2+4×10÷2=48
试一试:计算下列图形的面积
教法指导:(1)将图形分割成一个长方形和一个直角梯形;
(2)将这个不规则的图形补上一个边长为2cm的正方形后,得到一个直角梯形。
参考答案:(1)15×16+(12+34)×(16-4)÷2=516(cm2)
(2)(2+5.6)×8÷2=30.4(cm2)
此环节设计时间在40分钟左右(25分钟练习+15分钟互动讲解)。
一、判断题(对的在括号内打"√",错的打"×").
(1)正方形和长方形也是平行四边形。(
)
(2)等边三角形一定是等腰三角形,
等腰三角形也一定是等边三角形。(
)
(3)有一个角是锐角的三角形是锐角三角形。(
)
(4)三角形面积的大小与它的底和高有关,与它的形状和位置无关。(
)
(5)等底等高的两个三角形面积相等,形状也相同.(
)
二、填空题
(1)3小时36分
+
2小时48分
=
(
)小时(
)分
5600平方分米=(
)平方米
(2)一个等腰三角形的周长是18分米,腰是7分米,底边上的高是3分米,它的面积是(
)
(3)一个直角三角形的面积是16平方厘米,一条直角边长是4厘米,另一条直角边长是(
)厘米.
(4)平行四边形的面积是204平方分米,与它等底等高的三角形面积是(
)平方分米。
(5)一个梯形的面积是98平方分米,上底是12分米,下底是16分米,高是(
)
(6)一个三角形的底长6厘米,高4厘米,它的面积是(
)平方厘米。如果底和高都扩大2倍,面积是(
)平方厘米。
三、选择题
(1)如右图,图中一共有(
)个平行四边形。
A.
6
B.
7
C.
9
D.
18
(2)如右图,长方形和平行四边形的面积比较,(
)。
A.
长方形面积大。
B.
平行四边形面积大。
C.
一样大。
D.
无法比较。
(3)一块平行四边形的地,两条相邻的边长分别是50米和30米,其中一条边上对应的高是40米,这块地的面积是(
)平方米。
A.
1200
B.
2000
C.
1500
D.
无法确定
(4)一个三角形,把它的底缩小4倍,与它相对应的高扩大4倍,它的面积与原来的面积相比,结果是(
)。
A.
缩小16倍
B.
没有变化
C.
扩大4倍
D.
扩大16倍
(5)甲乙两个三角形如果底相等,而甲三角形的高是乙三角形高的2倍,那么甲三角形面积和乙三角形面积比较,面积(
)。
A.
相等
B.
甲是乙的2倍
C.
乙是甲的2倍
D.
比不出大小
解答题
1、求下列图形中的未知量
2、一块三角形地,底长38米,高是27米,如果每平方米收小麦0.7千克,这块地可以收小麦多少千克?
3、图中平行四边形的面积是24平方分米,求阴影部分的面积
4.将右图中的三角形ABC各条边都延长一倍至A′,B′,C′,连结这些点得到一新的三角形A′B′C′,若三角形ABC的面积是1,求三角形A′B′C′的面积。
参考答案:
一、(1)√
(2)×
(3)×
(4)√
(5)×
二、(1)6
24
56
(2)6平方分米
(3)8
(4)102
(5)7分米(6)12
48
三、(1)D
(2)A
(3)A
(4)B
(5)B
四、1、2.1dm
5.3cm
10.08
2、359.1千克
3、18平方分米
4、7
(此环节设计时间在5—10分钟内)
让学生回顾本节课所学的重点知识,以学生自我总结为主,学科教师引导为辅,为本次课做一个总结回顾
五年级第一学期期末数学模拟试卷
(完卷时间:80分钟
满分100分)
第一部分
计算(共42分)
1.直接写得数
8%
4.5×8=
3.28-0.8=
0.8÷5=
0.84÷0.7=
1.25×0.8=
46.8÷4.68=
2.5×4÷2.5×4=
2.8×0.1+2.8÷0.1=
2.解方程
6%
2(+5)=13.6
3.2-6.4=1.6
3.递等式计算(能简便计算的要简便计算,并写出必要的计算过程)
20%
6.4-5.4÷2.5
0.76×2.5×0.4
8080×1.25
18.5×5.8+5.2×18.5-18.5
1.2+36÷[1.44×(0.1-0.05)]
4.列综合式计算
8%
①8.4除2.1的商再加上3.6与2.5的积,和是多少?
②一个数的5倍减去2.5除以0.5的商,差是6.5,求这个数。
第二部分
概念(共22分)
1.填空
14%
①根据9.6×2.8=26.88填空。
9.6×0.28=(
)
268.8÷0.28=(
)
②5kg25g=(
)g
25cm2=(
)dm2
③一本《365夜》一共有a页,小明每天看8页,看了b天,一共看了(
)页,还剩(
)页没看。
④12.3÷9的商用简便记法记作(
),若商保留两位小数约是(
)。
⑤比大小,填>、<或=。
2.6÷3.02
2.6
5.4
5.4×0.72
⑥一个三角形的底边长3厘米,高4厘米,面积是(
)平方厘米,与它等底等高的平行四边形面积是(
)平方厘米。
⑦一个直角三角形的三条边分别是3厘米、4厘米和5厘米,这个三角形的面积是(
)平方厘米。
(
2
.
5
6
5
A
B
C
D
)⑧如右图(单位:厘米),用(
)厘米长
的铁丝可以围成这个平行四边形。
2.判断:(对的在括号里打√,错的打×)
4%
①22=2×2=4,所以a2=a×a=2a……………………………………
(
)
②的2倍加上6,可以写成2+6,这个式子不是方程。……………
(
)
③两个等底等高的三角形一定能拼成一个平行四边形。……………
(
)
(
(
)
)④把一个长方形木框拉成平行四边形,周长和面积都发生了改变。
3.选择:(在括号里填上正确答案的编号)
4%
①不笔算,估计下面结果比300大的算式是(
)。
A、17.5÷0.5
B、445.1×0.5
C、35.4×11
D、59.8×5
②两个数的商是7.8,当除数扩大6倍时,要使商不变,被除数应(
)
A、缩小6倍
B、扩大6倍
C、扩大7.8倍
D、不变
③三根5厘米长的小棒可以拼一个(
)三角形。
A、锐角
B、钝角
C、直角
D、等边
④一个梯形面积是16平方米,上底与下底的和是8米,那么高是(
)米。
A、2
B、4
C、6
D、8
第三部分
应用(共30分)
1.上海到北京大约有1200千米的路程,乘高铁从上海去北京只要4.8小时,从上海到北京的快速火车的平均速度只有100千米/时,求高铁的速度是快速火车的几倍?
2.学校组织秋游,五(1)班参加秋游的46人,比五(2)班参加的人数的1.2倍少2人,五(2)班参加秋游的有多少人?
3.某工程队修筑公路,前3天共修筑4.48千米,后7天平均每天修筑1.36千米。这个工程队平均每天修筑公路多少千米?
4.一个平行四边形的果园内栽了1800棵果树,平均每棵果树占地10平方米,这个平行四边形果园的底是360米,高是多少米?
5.上海电信公司通话的收费标准有两种:月租10元,通话费每分钟0.10元;无月租,通话费每分钟0.16元。若王老师每月的通话时间为150分钟,他选择哪种标准比较省钱?请列式说明。
第四部分
几何(共6分)
(
40
60
30
)1.计算下图阴影部分面积。(单位:dm)(6%)
参考答案:
第一部分
1、36
2.48
0.16
1.2
1
10
16
28.28
2、=1.8
=4
3、4.24
0.76
10100
185
501.2
4、①9.25
②2.3
第二部分
①2.688
960
②5025
0.25
③8b
a-8b
④
1.4
⑤<
>
⑥6
12
⑦6
⑧18
①×
②√
③×
④×
3、①C
②B
③D
④B
第三部分
1、2.5倍
2、40人
3、1.4千米
4、50米
5、有月租25元,无月租24元,选择无月租的收费标准
第四部分
900dm2
1
2
/
13
学科教师:
年
级:
辅导科目:
授课日期
时
间
主
题
期末复习(二)
教学内容
1.平行四边形、三角形、梯形及组合图形的面积;
2.期末模拟测试,查漏补缺.
(此环节设计时间在20—25分钟)
易错题整理
判断题(对的在括号内打"√",错的打"×").
(1)两个面积相等的三角形可以拼成一个平行四边形。(
)
(2)两个面积相等的三角形,它们的底和高一定相等。(
)
(3)梯形的面积等于梯形的上底加下底的和乘以高再除以2。(
)
(4)两个面积相等的梯形可以拼成一个平行四边形。(
)
(5)两个同底等高的三角形,形状相同,面积相等。(
)
二、填空题
(1)一个三角形的面积是4.8m2,与它等底等高的平行四边形的面积是(
)
(2)三角形一条边长是4.5分米,这条边上的高是8.6分米;另一条边长是3分米,则这条边上的高是(
).
(3)一个平行四边形,底为8分米,高2分米.如果底不变,高增加2分米,则面积增加(
);底和高都扩大5倍;它的面积扩大(
).
(4)一个梯形的面积是76平方厘米,下底是12厘米,上底是8厘米,梯形的高是(
)厘米。
(5)一个梯形的上底是2厘米,下底是4厘米,高是3厘米,求梯形面积的算式是(
)。当下底缩短到2厘米时,梯形变成(
),这时的面积是(
)平方厘米;当上底等于0时,梯形变成(
),这时的面积是(
)平方厘米。
三、选择题
(1)两个完全一样的三角形,可以拼成一个(
)。
A.长方形
B.正方形
C.梯形
D.平行四边形
(2)一个三角形,它的任意一条边上的高都是它的对称轴,这个三角形是(
)。
A.直角三角形
B.钝角三角形
C.等腰三角形
D.等边三角形
(3)一个直角三角形的两条直角边分别是3厘米和4厘米,斜边是5厘米,那么斜边上的高是(
)。
A.2
厘米
B.2.4厘米
C.3厘米
D.2.5厘米
(4)从平行四边形的一个顶点向对边可以作(
)条高。
A.一
B.两
C.四
D.无数
(
A
B
D
E
F
C
)(5)如图,ABCD是一个直角梯形,AECD是一个平行四边形,DF是梯形的高。两个阴影三角形的面积(
)。
A.=
B.
>
C.
<
D.无法比较
教法指导:先由学生做,同学之间互相批改,错误率高的题目由老师细致讲解,错误率低的题目可以让做对的学生向做错的学生讲解,老师做补充,做得都对的题目可以随机让学生讲解给大家听。
参考答案:
一、(1)×
(2)×
(3)√
(4)×
(5)×
二、(1)9.6m2
(2)12.9分米
(3)16平方分米
25倍
(4)7.6
(5)
平行四边形
6
三角形
6
三、(1)D
(2)C
(3)B
(4)B
(5)A
(此环节设计时间在40—50分钟)
例题1:一块长15米,宽10米的草地外面围一条宽1.5米的小路,求小路的面积?
(
15米
10米
)
教法指导:引导学生将实际问题转化成理论问题,正确求出外围长方形的长和宽,其实是分别加上小路宽的两倍,长是18米,宽是13米。小路的面积等于大长方形的面积减去小长方形的面积。也可以将小路分成四个窄点的长方形来求其面积。
参考答案:小路的面积为18×13-15×10=84(平方米)
试一试:如图,一个三角形的底长5米,如果底延长1米,那么面积就增加1.5平方米。那么原来三角形的面积是多少平方米?
????????
教法指导:通过图形可知延长底边,增加的是个三角形,求出这个三角形的高即求出了原来三角形的高,即可求出原来三角形的面积。这里需要注意,在已知三角形面积和底的前提下求三角形的高,不要先将面积乘以2.
参考答案:1.5×2÷1=3(m),3×5÷2=7.5(m2),即原来三角形的面积为7.5m2
例题2:下图中,三角形BCE的面积是6.3平方厘米,求直角梯形ABCD的面积。
(
A
2.4cm
B
2.8cm
F
C
D
E
3.2cm
)
教法指导:已知梯形的两个底,需要先求出梯形的高BC,在三角形BCE中,已知三角形的面积和高,可以求出底BC,即梯形ABCD的高。
参考答案:6.3×2÷2.8=4.5(cm),(2.4+3.2)×4.5÷2=12.6(cm2),即直角梯形ABCD的面积为12.6平方厘米。
试一试:下图的梯形的面积是9.57平方米,求阴影部分的面积。
教法指导:先由梯形的面积、上底和下底先求出梯形的高,这个高即为阴影部分的三角形以2为底的高。
参考答案:9.57×2÷(2+3.8)=3.3(m),3.3×2÷2=3.3(m2),即阴影部分的面积为3.3m2
例题3:如图,BD、DE、EC的长分别是2厘米,4厘米,2厘米,F是线段AE的中点,三角形ABC以BC为底的高为4厘米,求三角形DEF的面积。
教法指导:联结AD,则三角形ADE以DE为底的高与三角形ABC以BC为底的高相同,都为4厘米,先求出三角形ADE的面积,而三角形ADF和三角形EDF等底同高,故面积相等,所以三角形DEF的面积是三角形ADE面积的一半。
参考答案:三角形ADE的面积为4×4÷2=8(cm2),8÷2=4(cm2),及三角形DEF的面积为4cm2
试一试:已知BD长是2厘米,DC长是3厘米,E是AD的中点,如果三角形ABD的面积是5平方厘米,那么三角形DEC面积是多少?
教法指导:三角形ABD以BD为底和三角形ACD以CD为底同高,可以先求出三角形ACD的面积,再根据三角形ACE和三角形CDE等底同高求出三角形DEC的面积。
参考答案:三角形ACD的面积为5÷2×3=7.5(cm2),三角形CDE的面积为7.5÷2=3.75(cm2)
例题4:下图中,有四条线段的长度已知,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?
教法指导:联结AC,将阴影部分分割成两个钝角三角形,这两个钝角三角形都已知底和高,接下来就比较简便,解题的关键在于将这个不规则的图形分割成我们所熟悉的图形。
参考答案:7×8÷2+4×10÷2=48
试一试:计算下列图形的面积
教法指导:(1)将图形分割成一个长方形和一个直角梯形;
(2)将这个不规则的图形补上一个边长为2cm的正方形后,得到一个直角梯形。
参考答案:(1)15×16+(12+34)×(16-4)÷2=516(cm2)
(2)(2+5.6)×8÷2=30.4(cm2)
此环节设计时间在40分钟左右(25分钟练习+15分钟互动讲解)。
一、判断题(对的在括号内打"√",错的打"×").
(1)正方形和长方形也是平行四边形。(
)
(2)等边三角形一定是等腰三角形,
等腰三角形也一定是等边三角形。(
)
(3)有一个角是锐角的三角形是锐角三角形。(
)
(4)三角形面积的大小与它的底和高有关,与它的形状和位置无关。(
)
(5)等底等高的两个三角形面积相等,形状也相同.(
)
二、填空题
(1)3小时36分
+
2小时48分
=
(
)小时(
)分
5600平方分米=(
)平方米
(2)一个等腰三角形的周长是18分米,腰是7分米,底边上的高是3分米,它的面积是(
)
(3)一个直角三角形的面积是16平方厘米,一条直角边长是4厘米,另一条直角边长是(
)厘米.
(4)平行四边形的面积是204平方分米,与它等底等高的三角形面积是(
)平方分米。
(5)一个梯形的面积是98平方分米,上底是12分米,下底是16分米,高是(
)
(6)一个三角形的底长6厘米,高4厘米,它的面积是(
)平方厘米。如果底和高都扩大2倍,面积是(
)平方厘米。
三、选择题
(1)如右图,图中一共有(
)个平行四边形。
A.
6
B.
7
C.
9
D.
18
(2)如右图,长方形和平行四边形的面积比较,(
)。
A.
长方形面积大。
B.
平行四边形面积大。
C.
一样大。
D.
无法比较。
(3)一块平行四边形的地,两条相邻的边长分别是50米和30米,其中一条边上对应的高是40米,这块地的面积是(
)平方米。
A.
1200
B.
2000
C.
1500
D.
无法确定
(4)一个三角形,把它的底缩小4倍,与它相对应的高扩大4倍,它的面积与原来的面积相比,结果是(
)。
A.
缩小16倍
B.
没有变化
C.
扩大4倍
D.
扩大16倍
(5)甲乙两个三角形如果底相等,而甲三角形的高是乙三角形高的2倍,那么甲三角形面积和乙三角形面积比较,面积(
)。
A.
相等
B.
甲是乙的2倍
C.
乙是甲的2倍
D.
比不出大小
解答题
1、求下列图形中的未知量
2、一块三角形地,底长38米,高是27米,如果每平方米收小麦0.7千克,这块地可以收小麦多少千克?
3、图中平行四边形的面积是24平方分米,求阴影部分的面积
4.将右图中的三角形ABC各条边都延长一倍至A′,B′,C′,连结这些点得到一新的三角形A′B′C′,若三角形ABC的面积是1,求三角形A′B′C′的面积。
参考答案:
一、(1)√
(2)×
(3)×
(4)√
(5)×
二、(1)6
24
56
(2)6平方分米
(3)8
(4)102
(5)7分米(6)12
48
三、(1)D
(2)A
(3)A
(4)B
(5)B
四、1、2.1dm
5.3cm
10.08
2、359.1千克
3、18平方分米
4、7
(此环节设计时间在5—10分钟内)
让学生回顾本节课所学的重点知识,以学生自我总结为主,学科教师引导为辅,为本次课做一个总结回顾
五年级第一学期期末数学模拟试卷
(完卷时间:80分钟
满分100分)
第一部分
计算(共42分)
1.直接写得数
8%
4.5×8=
3.28-0.8=
0.8÷5=
0.84÷0.7=
1.25×0.8=
46.8÷4.68=
2.5×4÷2.5×4=
2.8×0.1+2.8÷0.1=
2.解方程
6%
2(+5)=13.6
3.2-6.4=1.6
3.递等式计算(能简便计算的要简便计算,并写出必要的计算过程)
20%
6.4-5.4÷2.5
0.76×2.5×0.4
8080×1.25
18.5×5.8+5.2×18.5-18.5
1.2+36÷[1.44×(0.1-0.05)]
4.列综合式计算
8%
①8.4除2.1的商再加上3.6与2.5的积,和是多少?
②一个数的5倍减去2.5除以0.5的商,差是6.5,求这个数。
第二部分
概念(共22分)
1.填空
14%
①根据9.6×2.8=26.88填空。
9.6×0.28=(
)
268.8÷0.28=(
)
②5kg25g=(
)g
25cm2=(
)dm2
③一本《365夜》一共有a页,小明每天看8页,看了b天,一共看了(
)页,还剩(
)页没看。
④12.3÷9的商用简便记法记作(
),若商保留两位小数约是(
)。
⑤比大小,填>、<或=。
2.6÷3.02
2.6
5.4
5.4×0.72
⑥一个三角形的底边长3厘米,高4厘米,面积是(
)平方厘米,与它等底等高的平行四边形面积是(
)平方厘米。
⑦一个直角三角形的三条边分别是3厘米、4厘米和5厘米,这个三角形的面积是(
)平方厘米。
(
2
.
5
6
5
A
B
C
D
)⑧如右图(单位:厘米),用(
)厘米长
的铁丝可以围成这个平行四边形。
2.判断:(对的在括号里打√,错的打×)
4%
①22=2×2=4,所以a2=a×a=2a……………………………………
(
)
②的2倍加上6,可以写成2+6,这个式子不是方程。……………
(
)
③两个等底等高的三角形一定能拼成一个平行四边形。……………
(
)
(
(
)
)④把一个长方形木框拉成平行四边形,周长和面积都发生了改变。
3.选择:(在括号里填上正确答案的编号)
4%
①不笔算,估计下面结果比300大的算式是(
)。
A、17.5÷0.5
B、445.1×0.5
C、35.4×11
D、59.8×5
②两个数的商是7.8,当除数扩大6倍时,要使商不变,被除数应(
)
A、缩小6倍
B、扩大6倍
C、扩大7.8倍
D、不变
③三根5厘米长的小棒可以拼一个(
)三角形。
A、锐角
B、钝角
C、直角
D、等边
④一个梯形面积是16平方米,上底与下底的和是8米,那么高是(
)米。
A、2
B、4
C、6
D、8
第三部分
应用(共30分)
1.上海到北京大约有1200千米的路程,乘高铁从上海去北京只要4.8小时,从上海到北京的快速火车的平均速度只有100千米/时,求高铁的速度是快速火车的几倍?
2.学校组织秋游,五(1)班参加秋游的46人,比五(2)班参加的人数的1.2倍少2人,五(2)班参加秋游的有多少人?
3.某工程队修筑公路,前3天共修筑4.48千米,后7天平均每天修筑1.36千米。这个工程队平均每天修筑公路多少千米?
4.一个平行四边形的果园内栽了1800棵果树,平均每棵果树占地10平方米,这个平行四边形果园的底是360米,高是多少米?
5.上海电信公司通话的收费标准有两种:月租10元,通话费每分钟0.10元;无月租,通话费每分钟0.16元。若王老师每月的通话时间为150分钟,他选择哪种标准比较省钱?请列式说明。
第四部分
几何(共6分)
(
40
60
30
)1.计算下图阴影部分面积。(单位:dm)(6%)
参考答案:
第一部分
1、36
2.48
0.16
1.2
1
10
16
28.28
2、=1.8
=4
3、4.24
0.76
10100
185
501.2
4、①9.25
②2.3
第二部分
①2.688
960
②5025
0.25
③8b
a-8b
④
1.4
⑤<
>
⑥6
12
⑦6
⑧18
①×
②√
③×
④×
3、①C
②B
③D
④B
第三部分
1、2.5倍
2、40人
3、1.4千米
4、50米
5、有月租25元,无月租24元,选择无月租的收费标准
第四部分
900dm2
1
2
/
13
同课章节目录
