苏科版七年级数学上册导学案2.5有理数的加法与减法(1)
文档属性
| 名称 | 苏科版七年级数学上册导学案2.5有理数的加法与减法(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 76.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 00:00:00 | ||
图片预览




文档简介
第二章
有理数
课题:2.5有理数的加法与减法(1)
学习目标
1.通过课本中“足球净胜球”的实际问题感受引入负数后加法结果的变化.
2.通过课本中的“数学实验室”,借助数形结合的思想方法了解有理数的加法过程.
3.阅读课本中的有理数加法法则,并初步了解其应用.
【导学指导】:
一、知识链接:
有理数加法法则
1.同号两数相加,取__相同_____的符号,并把绝对值___相加_____.
(1)两个正数相加的结果必是___正____数.
(2)两个负数相加的结果必是___负____数.
2.异号两数相加
(1)两数的绝对值相等,和为___0___,即两个互为__相反数___的数相加等于___0____.
(2)两数的绝对值不等,取__绝对值较大加数___的符号,并用较大的绝对值__减去__较小的绝对值.
①正数的绝对值大,异号两数相加的结果必是___正____数;
②负数的绝对值大,异号两数相加的结果必是___负____数.
3.-个数与0相加,结果__仍是这个数_____.
二、自主学习
例题精讲
例1
计算:
(1)(+2)+(-11);
(2)(+20)+(+12);
=-(11-2)
=+(20+12)
=-9
=32
(3)(-1)+(-);
(4)(-3.4)+4.3.
=
-(1+)
=+(4.3-3.4)
=
=0.9
例2
利用有理数的加法计算解下面各题:
(1)潜水员先潜入水下25米,然后又上升18米,此时潜水员在水下什么位置?
(2)某仓库原有粮食52
t,运出32
t,现在仓库共有多少粮食?
解:(1)
(-25)+18=-7
答:此时潜水员在水下7米处
(2)52+(-32)=20
答:现在仓库共有粮食20t
三、巩固知识
[典型问题]
(1)
(+5)+(+7)=________;
(2)
(-3)+(-8)=_______;
(3)
(+3)+(-8)=________;
(4)
(-3)+(-15)=_______;
(5)
0+(-5)=________;
(6)
(-7)+(+7)=_______.
2.比-3大-6的数为_______;先上升20米,再上升-10米,则一共上升_______米.
3.已知一个数为-5,另一个数比它的相反数大4,则这两数的和为_______.
4.若两数的和为负数,则这两个数不可能
(
)
A.同正
B.同负
C.一正一负
D.有一个为0
5.计算:
(1);
(2);
(3);
(4);
(5)(+4.85)+(-3.25);
(6)(-3.1)+(+6.9);
(7);
(8)
.
6.某同学在一条由东向西的跑道上,先向东走了20米,又向西走了30米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
7.存折中原有550元,取出260元后,又存入150元,现在存折中还有多少元钱?
[四基训练]
8.在1,-1,-2这三个数中,任意两数之和的最大值是
(
)
A.1
B.0
C.-1
D.-3
9.已知两个有理数的和为正数,则这两个有理数
(
)
A.都为正数
B.都不为零
C.至少有一个为负数
D.至少有一个为正数
10.计算:
(1)+(+3)=__________;
(2)(-3)+2=_________;
(3)(-)+(-)=_________;
(4)(-5)
+=__________.
11.用“>”或“<”填空:
(1)若m>0,n>0,则m+n_________0;
(2)若m<0,n<0,则m+n_________0;
(3)若m<0,n>0,且,则m+n_________0;
(4)若m>0,n<0,且,则m+n__________0.
12.若,,则a=______,b=______,a+b=_______.
13.计算:
(1)67+(-73);
(2);
(3).
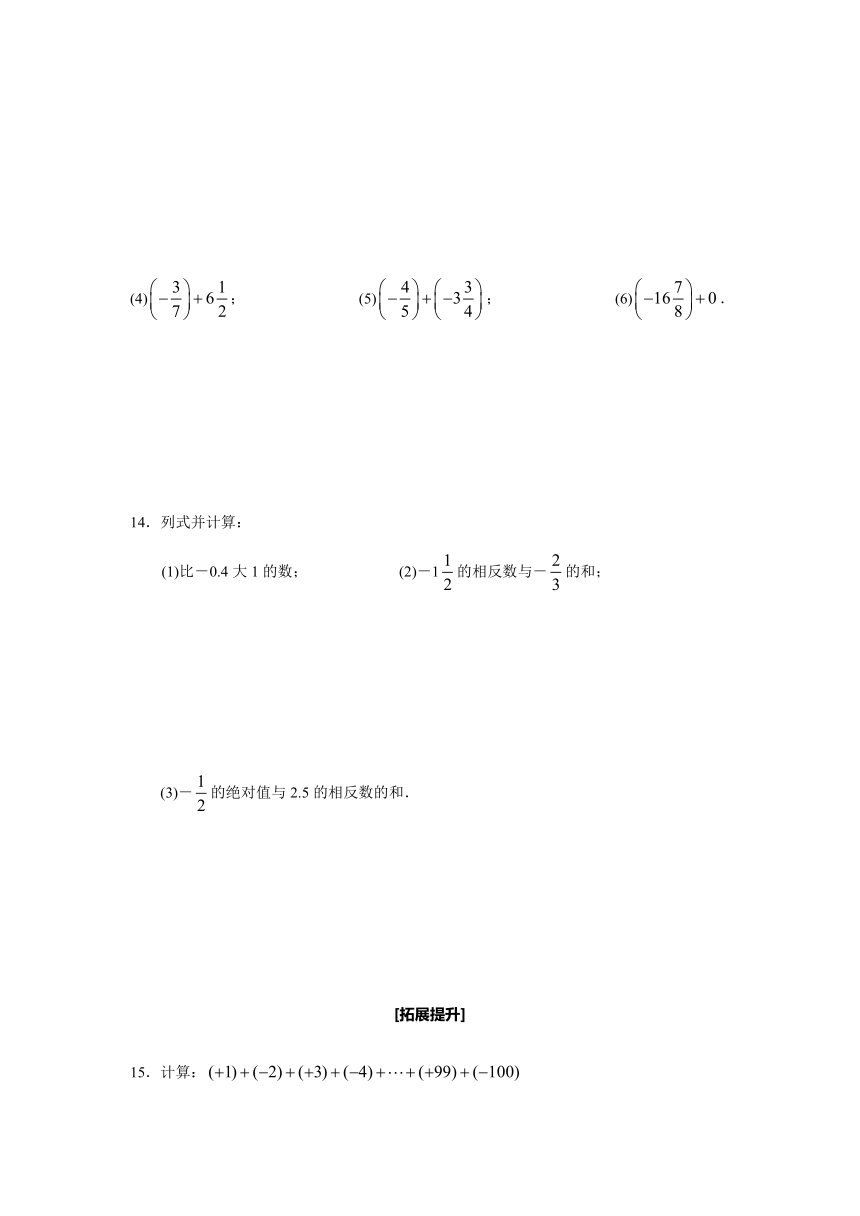
(4);
(5);
(6).
14.列式并计算:
(1)比-0.4大1的数;
(2)-1的相反数与-的和;
(3)-的绝对值与2.5的相反数的和.
[拓展提升]
15.计算:
16.小王上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票1000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)
根据上表回答问题:(1)星期二收盘时,该股票每股多少元?
(2)一周内该股票收盘时的最高价,最低价分别是多少?
答案:
(1)
(+5)+(+7)=__12______;
(2)
(-3)+(-8)=___-11____;
(3)
(+3)+(-8)=__-5_____;
(4)
(-3)+(-15)=__-18_____;
(5)
0+(-5)=__-5______;
(6)
(-7)+(+7)=___0____.
2.比-3大-6的数为__-9_____;先上升20米,再上升-10米,则一共上升___10____米.
3.已知一个数为-5,另一个数比它的相反数大4,则这两数的和为___4____.
4.若两数的和为负数,则这两个数不可能
(
A
)
A.同正
B.同负
C.一正一负
D.有一个为0
5.计算:
(1);
(2);
(3);
=
=
=
=)
=)
=)
=
=
(4);
(5)(+4.85)+(-3.25);
(6)(-3.1)+(+6.9);
=7+9
=+(4.85-3.25)
=+(6.9-3.1)
=16
=1.6
=3.8
(7);
(8)
.
=
=0
6.某同学在一条由东向西的跑道上,先向东走了20米,又向西走了30米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
解:20+(-30)=-10
答:位于原来位置的西边,与原来位置相距10米
7.存折中原有550元,取出260元后,又存入150元,现在存折中还有多少元钱?
解:550+(-260)+150=440
答:现在存折中还有440元钱
[四基训练]
8.在1,-1,-2这三个数中,任意两数之和的最大值是
(
B
)
A.1
B.0
C.-1
D.-3
9.已知两个有理数的和为正数,则这两个有理数
(
D
)
A.都为正数
B.都不为零
C.至少有一个为负数
D.至少有一个为正数
10.计算:
(1)+(+3)=_3.5_________;
(2)(-3)+2=___-1______;
(3)(-)+(-)=___-2______;
(4)(-5)
+=___4_______.
11.用“>”或“<”填空:
(1)若m>0,n>0,则m+n___>______0;
(2)若m<0,n<0,则m+n___<______0;
(3)若m<0,n>0,且,则m+n___<______0;
(4)若m>0,n<0,且,则m+n____>______0.
12.若,,则a=______,b=______,a+b=__或_____.
13.计算:
(1)67+(-73);
(2);
(3).
=-(73-67)
=+(1.75-1.25)
=
=-6
=0.5
=
=
(4);
(5);
(6).
=
=
=-16
=
=
=
14.列式并计算:
(1)比-0.4大1的数;
(2)-1的相反数与-的和;
解:-0.4+1=0.6
解:
(3)-的绝对值与2.5的相反数的和.
解:0.5+(-2.5)=-2
[拓展提升]
15.计算:
解:
=[(+1)+(-2)]+
[(+3)+(-4)]+---+
[(+99)+(-100)]
=(-1)+(-1)
+---+(-1)
=-50
16.小王上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票1000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)
根据上表回答问题:(1)星期二收盘时,该股票每股多少元?
(2)一周内该股票收盘时的最高价,最低价分别是多少?
解:(1)25+2+(-0.5)=26.5
答:星期二收盘时,该股票每股26.5元
(2)星期一收盘时,该股票每股
25+2=27(元)
星期二收盘时,该股票每股
27+(-0.5)=26.5(元)
星期三收盘时,该股票每股
26.5+1.5=28(元)
星期四收盘时,该股票每股
28+(-1.8)=26.2(元)
星期五收盘时,该股票每股
26.2+0.8=27(元)
答:一周内该股票收盘时的最高价是28元,最低价是26.2元.
有理数
课题:2.5有理数的加法与减法(1)
学习目标
1.通过课本中“足球净胜球”的实际问题感受引入负数后加法结果的变化.
2.通过课本中的“数学实验室”,借助数形结合的思想方法了解有理数的加法过程.
3.阅读课本中的有理数加法法则,并初步了解其应用.
【导学指导】:
一、知识链接:
有理数加法法则
1.同号两数相加,取__相同_____的符号,并把绝对值___相加_____.
(1)两个正数相加的结果必是___正____数.
(2)两个负数相加的结果必是___负____数.
2.异号两数相加
(1)两数的绝对值相等,和为___0___,即两个互为__相反数___的数相加等于___0____.
(2)两数的绝对值不等,取__绝对值较大加数___的符号,并用较大的绝对值__减去__较小的绝对值.
①正数的绝对值大,异号两数相加的结果必是___正____数;
②负数的绝对值大,异号两数相加的结果必是___负____数.
3.-个数与0相加,结果__仍是这个数_____.
二、自主学习
例题精讲
例1
计算:
(1)(+2)+(-11);
(2)(+20)+(+12);
=-(11-2)
=+(20+12)
=-9
=32
(3)(-1)+(-);
(4)(-3.4)+4.3.
=
-(1+)
=+(4.3-3.4)
=
=0.9
例2
利用有理数的加法计算解下面各题:
(1)潜水员先潜入水下25米,然后又上升18米,此时潜水员在水下什么位置?
(2)某仓库原有粮食52
t,运出32
t,现在仓库共有多少粮食?
解:(1)
(-25)+18=-7
答:此时潜水员在水下7米处
(2)52+(-32)=20
答:现在仓库共有粮食20t
三、巩固知识
[典型问题]
(1)
(+5)+(+7)=________;
(2)
(-3)+(-8)=_______;
(3)
(+3)+(-8)=________;
(4)
(-3)+(-15)=_______;
(5)
0+(-5)=________;
(6)
(-7)+(+7)=_______.
2.比-3大-6的数为_______;先上升20米,再上升-10米,则一共上升_______米.
3.已知一个数为-5,另一个数比它的相反数大4,则这两数的和为_______.
4.若两数的和为负数,则这两个数不可能
(
)
A.同正
B.同负
C.一正一负
D.有一个为0
5.计算:
(1);
(2);
(3);
(4);
(5)(+4.85)+(-3.25);
(6)(-3.1)+(+6.9);
(7);
(8)
.
6.某同学在一条由东向西的跑道上,先向东走了20米,又向西走了30米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
7.存折中原有550元,取出260元后,又存入150元,现在存折中还有多少元钱?
[四基训练]
8.在1,-1,-2这三个数中,任意两数之和的最大值是
(
)
A.1
B.0
C.-1
D.-3
9.已知两个有理数的和为正数,则这两个有理数
(
)
A.都为正数
B.都不为零
C.至少有一个为负数
D.至少有一个为正数
10.计算:
(1)+(+3)=__________;
(2)(-3)+2=_________;
(3)(-)+(-)=_________;
(4)(-5)
+=__________.
11.用“>”或“<”填空:
(1)若m>0,n>0,则m+n_________0;
(2)若m<0,n<0,则m+n_________0;
(3)若m<0,n>0,且,则m+n_________0;
(4)若m>0,n<0,且,则m+n__________0.
12.若,,则a=______,b=______,a+b=_______.
13.计算:
(1)67+(-73);
(2);
(3).
(4);
(5);
(6).
14.列式并计算:
(1)比-0.4大1的数;
(2)-1的相反数与-的和;
(3)-的绝对值与2.5的相反数的和.
[拓展提升]
15.计算:
16.小王上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票1000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)
根据上表回答问题:(1)星期二收盘时,该股票每股多少元?
(2)一周内该股票收盘时的最高价,最低价分别是多少?
答案:
(1)
(+5)+(+7)=__12______;
(2)
(-3)+(-8)=___-11____;
(3)
(+3)+(-8)=__-5_____;
(4)
(-3)+(-15)=__-18_____;
(5)
0+(-5)=__-5______;
(6)
(-7)+(+7)=___0____.
2.比-3大-6的数为__-9_____;先上升20米,再上升-10米,则一共上升___10____米.
3.已知一个数为-5,另一个数比它的相反数大4,则这两数的和为___4____.
4.若两数的和为负数,则这两个数不可能
(
A
)
A.同正
B.同负
C.一正一负
D.有一个为0
5.计算:
(1);
(2);
(3);
=
=
=
=)
=)
=)
=
=
(4);
(5)(+4.85)+(-3.25);
(6)(-3.1)+(+6.9);
=7+9
=+(4.85-3.25)
=+(6.9-3.1)
=16
=1.6
=3.8
(7);
(8)
.
=
=0
6.某同学在一条由东向西的跑道上,先向东走了20米,又向西走了30米,能否确定他现在位于原来位置的哪个方向,与原来位置相距多少米?
解:20+(-30)=-10
答:位于原来位置的西边,与原来位置相距10米
7.存折中原有550元,取出260元后,又存入150元,现在存折中还有多少元钱?
解:550+(-260)+150=440
答:现在存折中还有440元钱
[四基训练]
8.在1,-1,-2这三个数中,任意两数之和的最大值是
(
B
)
A.1
B.0
C.-1
D.-3
9.已知两个有理数的和为正数,则这两个有理数
(
D
)
A.都为正数
B.都不为零
C.至少有一个为负数
D.至少有一个为正数
10.计算:
(1)+(+3)=_3.5_________;
(2)(-3)+2=___-1______;
(3)(-)+(-)=___-2______;
(4)(-5)
+=___4_______.
11.用“>”或“<”填空:
(1)若m>0,n>0,则m+n___>______0;
(2)若m<0,n<0,则m+n___<______0;
(3)若m<0,n>0,且,则m+n___<______0;
(4)若m>0,n<0,且,则m+n____>______0.
12.若,,则a=______,b=______,a+b=__或_____.
13.计算:
(1)67+(-73);
(2);
(3).
=-(73-67)
=+(1.75-1.25)
=
=-6
=0.5
=
=
(4);
(5);
(6).
=
=
=-16
=
=
=
14.列式并计算:
(1)比-0.4大1的数;
(2)-1的相反数与-的和;
解:-0.4+1=0.6
解:
(3)-的绝对值与2.5的相反数的和.
解:0.5+(-2.5)=-2
[拓展提升]
15.计算:
解:
=[(+1)+(-2)]+
[(+3)+(-4)]+---+
[(+99)+(-100)]
=(-1)+(-1)
+---+(-1)
=-50
16.小王上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票1000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)
根据上表回答问题:(1)星期二收盘时,该股票每股多少元?
(2)一周内该股票收盘时的最高价,最低价分别是多少?
解:(1)25+2+(-0.5)=26.5
答:星期二收盘时,该股票每股26.5元
(2)星期一收盘时,该股票每股
25+2=27(元)
星期二收盘时,该股票每股
27+(-0.5)=26.5(元)
星期三收盘时,该股票每股
26.5+1.5=28(元)
星期四收盘时,该股票每股
28+(-1.8)=26.2(元)
星期五收盘时,该股票每股
26.2+0.8=27(元)
答:一周内该股票收盘时的最高价是28元,最低价是26.2元.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
