人教版八年级上册数学导学案:11.2.1 三角形的内角(无答案)
文档属性
| 名称 | 人教版八年级上册数学导学案:11.2.1 三角形的内角(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 71.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 00:00:00 | ||
图片预览

文档简介
11.2.1
三角形的内角
学习目标:
(1)学会利用已学的相交线与平行线等相关性质证明三角形的内角和定理;
(2)初步了解什么是几何证明,并感受证明几何问题的基本结构和推导过程;
(3)基本学会利用三角形内角和定理解决生活中的实际问题。
新课导学:
试一试,下面的练习,你还会做吗?
如图1(1),已知:直线上有一点A,过点A作射线AM、AN;
1、若∠DAM=30°,∠EAN=70°,则∠1等于
度。
2、若在AM上任取一点B,过点B作BC∥DE交AN于点C如图1(2),
则:(1)∠2等于
度,根据:
(2)∠3等于
度,根据:
(3)∠1+∠2+∠3等于
度。
(三)问题:任剪一个三角形,按下列要求进行实验
(1)先剪下∠B和∠C(如图2),然后把它们与∠A
拼合在一起,就得到一个平角.有多少种不同的拼合
方法?请你把这些不同的方法分别拼出来;这个实验
说明什么?你会证明吗?
实验说明:
(2)在(1)中你觉得哪几种拼合的结果有助于发现证明三角形内角和等于180度思路?它们有什么共同的特点?
(四)证明三角形内角和定理:三角形的三个内角和等于180?;
已知:如图3,三角形ABC
求证:∠A+∠B+∠C=
证明:(方法一)
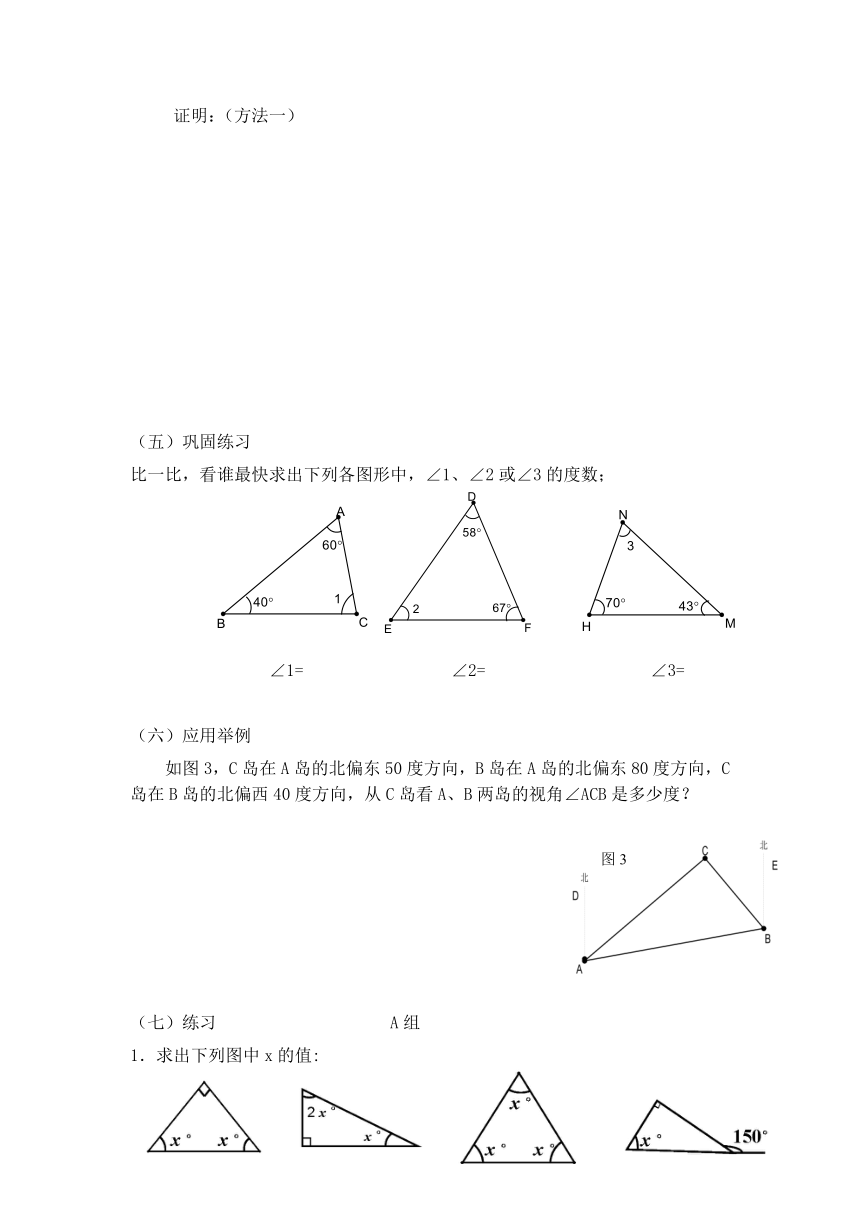
(五)巩固练习
比一比,看谁最快求出下列各图形中,∠1、∠2或∠3的度数;
∠1=
∠2=
∠3=
(六)应用举例
如图3,C岛在A岛的北偏东50度方向,B岛在A岛的北偏东80度方向,C岛在B岛的北偏西40度方向,从C岛看A、B两岛的视角∠ACB是多少度?
(七)练习
A组
1.求出下列图中x的值:
x=
x=
x=
x=
2、求下列图形中的∠1、∠2的度数:
(1)
(2)
(3)
AB∥CD
∠1=
?
∠1=
?
∠1=
?
∠2=
?
∠2=
?
∠2=
?
3、如图,从A处观测C处时仰角∠CAD=30?,从B处
观测C处时仰角为∠CBD=45?,则∠CBA是
度,
从C处观测A,B两处时视角∠ACB是
度。
B
组
4、如图,一种滑翔伞的形状是左右对称的四边形ABCD,
其中∠A=150度,∠B=∠D=40度,求∠C的度数。
5、如图,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC的度数。
6、在三角形ABC中∠B=∠A+10°,∠C=∠B+10°,求三角形ABC的各内角的度数;
7、如图,AB∥CD,∠A=40°,∠D=45°,求∠1和∠2;
8、如图AB∥CD,∠A=45°,∠C
=∠E,求∠C;
9、如图3,A岛在B岛的北偏东50度方向,C岛在B岛的北偏东80度
方向,C岛在A
岛的现偏东30度方向,从C岛看A、B两岛
的视角∠ACB是多少度?
三角形的内角
学习目标:
(1)学会利用已学的相交线与平行线等相关性质证明三角形的内角和定理;
(2)初步了解什么是几何证明,并感受证明几何问题的基本结构和推导过程;
(3)基本学会利用三角形内角和定理解决生活中的实际问题。
新课导学:
试一试,下面的练习,你还会做吗?
如图1(1),已知:直线上有一点A,过点A作射线AM、AN;
1、若∠DAM=30°,∠EAN=70°,则∠1等于
度。
2、若在AM上任取一点B,过点B作BC∥DE交AN于点C如图1(2),
则:(1)∠2等于
度,根据:
(2)∠3等于
度,根据:
(3)∠1+∠2+∠3等于
度。
(三)问题:任剪一个三角形,按下列要求进行实验
(1)先剪下∠B和∠C(如图2),然后把它们与∠A
拼合在一起,就得到一个平角.有多少种不同的拼合
方法?请你把这些不同的方法分别拼出来;这个实验
说明什么?你会证明吗?
实验说明:
(2)在(1)中你觉得哪几种拼合的结果有助于发现证明三角形内角和等于180度思路?它们有什么共同的特点?
(四)证明三角形内角和定理:三角形的三个内角和等于180?;
已知:如图3,三角形ABC
求证:∠A+∠B+∠C=
证明:(方法一)
(五)巩固练习
比一比,看谁最快求出下列各图形中,∠1、∠2或∠3的度数;
∠1=
∠2=
∠3=
(六)应用举例
如图3,C岛在A岛的北偏东50度方向,B岛在A岛的北偏东80度方向,C岛在B岛的北偏西40度方向,从C岛看A、B两岛的视角∠ACB是多少度?
(七)练习
A组
1.求出下列图中x的值:
x=
x=
x=
x=
2、求下列图形中的∠1、∠2的度数:
(1)
(2)
(3)
AB∥CD
∠1=
?
∠1=
?
∠1=
?
∠2=
?
∠2=
?
∠2=
?
3、如图,从A处观测C处时仰角∠CAD=30?,从B处
观测C处时仰角为∠CBD=45?,则∠CBA是
度,
从C处观测A,B两处时视角∠ACB是
度。
B
组
4、如图,一种滑翔伞的形状是左右对称的四边形ABCD,
其中∠A=150度,∠B=∠D=40度,求∠C的度数。
5、如图,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC的度数。
6、在三角形ABC中∠B=∠A+10°,∠C=∠B+10°,求三角形ABC的各内角的度数;
7、如图,AB∥CD,∠A=40°,∠D=45°,求∠1和∠2;
8、如图AB∥CD,∠A=45°,∠C
=∠E,求∠C;
9、如图3,A岛在B岛的北偏东50度方向,C岛在B岛的北偏东80度
方向,C岛在A
岛的现偏东30度方向,从C岛看A、B两岛
的视角∠ACB是多少度?
