人教版八年级上册数学12.2三角形全等的判定(HL)教案(第1课时 表格式)
文档属性
| 名称 | 人教版八年级上册数学12.2三角形全等的判定(HL)教案(第1课时 表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 166.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 00:00:00 | ||
图片预览

文档简介
课题(内容)
12.2三角形全等的判定(HL)
课时数
1
第
1
课时
课型
新授课
三维目标
知识与能力:1、理解直角三角形全等的判定方法“HL”,并能灵活选择方法判定三角形全等;
2.通过独立思考、小组合作、展示质疑,体会探索数学结论的过程,发展合情推理能力;
3.
极度热情、高度责任、自动自发、享受成功。
过程与方法:学练结合、小组合作
情感态度与价值观:培养学生良好的品德和学习数学的兴趣爱好
重难点
教学重点:运用直角三角形全等的条件解决一些实际问题。
教学难点:
熟练运用直角三角形全等的条件解决一些实际问题。
资源准备
直尺、三角板、课件
学案
导
案
一、自主学习
1、复习思考
、判定两个三角形全等的方法:
、
、
、
、如图,Rt△ABC中,直角边是
、
,斜边是
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,则△ABC与△DEF
(填“全等”或“不全等”
)根据
(用简写法)
②若∠A=∠D,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
)根据
(用简写法)
③若AB=DE,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
)根据
(用简写法)
④若AB=DE,BC=EF,AC=DF则△ABC与△DEF
(填“全等”或“不全等”
)根据
(用简写法)
2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC
求作:Rt△,
使=90°,
=AB,
=BC
作法:
(2)
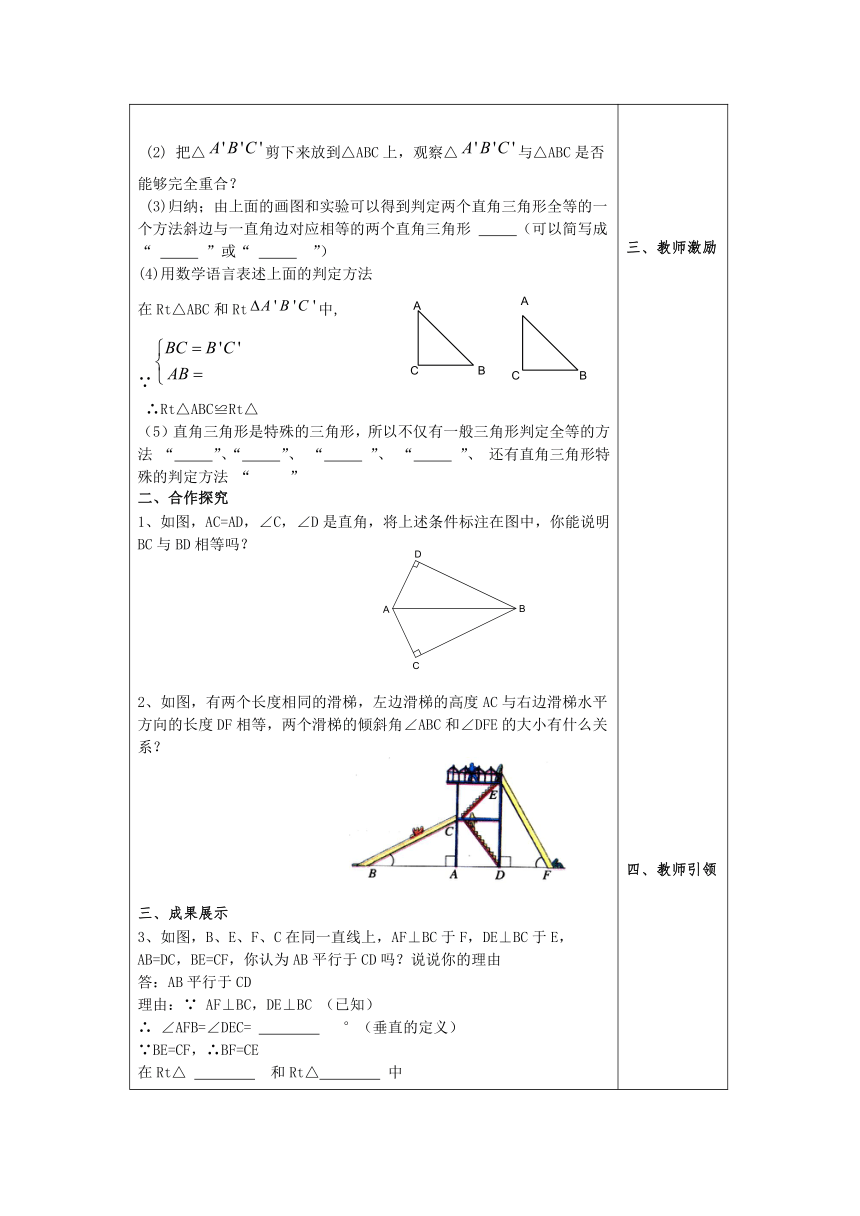
把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法斜边与一直角边对应相等的两个直角三角形
(可以简写成“
”或“
”)
(4)用数学语言表述上面的判定方法
在Rt△ABC和Rt中,
∵
∴Rt△ABC≌Rt△
(5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法
“
”、“
”、
“
”、
“
”、
还有直角三角形特殊的判定方法
“
”
二、合作探究
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
2、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
三、成果展示
3、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵
AF⊥BC,DE⊥BC
(已知)
∴
∠AFB=∠DEC=
°(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△
和Rt△
中
∵∴
≌
(
)
∴
=
(
)
∴
(内错角相等,两直线平行)
四、拓展延伸
如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
五、达标检测
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5)
若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
一、教师导学
二、教师参与
三、教师激励
四、教师引领
五、教师测评
教学反思
作业批改及辅导记录
12.2三角形全等的判定(HL)
课时数
1
第
1
课时
课型
新授课
三维目标
知识与能力:1、理解直角三角形全等的判定方法“HL”,并能灵活选择方法判定三角形全等;
2.通过独立思考、小组合作、展示质疑,体会探索数学结论的过程,发展合情推理能力;
3.
极度热情、高度责任、自动自发、享受成功。
过程与方法:学练结合、小组合作
情感态度与价值观:培养学生良好的品德和学习数学的兴趣爱好
重难点
教学重点:运用直角三角形全等的条件解决一些实际问题。
教学难点:
熟练运用直角三角形全等的条件解决一些实际问题。
资源准备
直尺、三角板、课件
学案
导
案
一、自主学习
1、复习思考
、判定两个三角形全等的方法:
、
、
、
、如图,Rt△ABC中,直角边是
、
,斜边是
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,则△ABC与△DEF
(填“全等”或“不全等”
)根据
(用简写法)
②若∠A=∠D,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
)根据
(用简写法)
③若AB=DE,BC=EF,则△ABC与△DEF
(填“全等”或“不全等”
)根据
(用简写法)
④若AB=DE,BC=EF,AC=DF则△ABC与△DEF
(填“全等”或“不全等”
)根据
(用简写法)
2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC
求作:Rt△,
使=90°,
=AB,
=BC
作法:
(2)
把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法斜边与一直角边对应相等的两个直角三角形
(可以简写成“
”或“
”)
(4)用数学语言表述上面的判定方法
在Rt△ABC和Rt中,
∵
∴Rt△ABC≌Rt△
(5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法
“
”、“
”、
“
”、
“
”、
还有直角三角形特殊的判定方法
“
”
二、合作探究
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
2、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
三、成果展示
3、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵
AF⊥BC,DE⊥BC
(已知)
∴
∠AFB=∠DEC=
°(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△
和Rt△
中
∵∴
≌
(
)
∴
=
(
)
∴
(内错角相等,两直线平行)
四、拓展延伸
如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
五、达标检测
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5)
若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
一、教师导学
二、教师参与
三、教师激励
四、教师引领
五、教师测评
教学反思
作业批改及辅导记录
