人教版八年级数学上册11.2.1 三角形的内角能力提升卷(word 版 含答案)
文档属性
| 名称 | 人教版八年级数学上册11.2.1 三角形的内角能力提升卷(word 版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 261.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 11:25:03 | ||
图片预览



文档简介
人教版八年级数学上册
11.2.1.2直角三角形两锐角互余
能力提升卷
一、选择题(共10小题,3
10=30)
1.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个
B.2个
C.3个
D.4个
2.如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.85°
3.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E,若∠A=54°,∠B=48°,则∠CDE的度数为( )
A.44°
B.40°
C.39°
D.38°
4.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为(
)
A.50°
B.45°
C.40°
D.30°
5.如图,在Rt△ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB
的平分线,交边BC于点D,过点C作△ACD中AD
边上的高线CE,则∠ECD的度数为( )
A.63°
B.45°
C.27°
D.18°
6.
若一个三角形三个内角的度数之比为1∶2∶3,则这个三角形是( )
A.锐角三角形
B.等边三角形
C.钝角三角形
D.直角三角形
7.在△ABC中,∠A=∠B+∠C,∠B=2∠C-6°,则∠C的度数为( )
A.90°
B.58°
C.54°
D.32°
8.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A=∠B=∠C
C.∠A:∠B:∠C=1:3:4
D.∠A=2∠B=3∠C
9.如图,在△ABC中,∠ABC=62°,BD是角平分线,CE是高,BD与CE相交于点O,则∠BOC的度数是( )
A.118°
B.119°
C.120°
D.121°
10.在下列条件中:①∠A=∠C-∠B,②∠A∶∠B∶∠C=2∶3∶5,③∠A=90°-∠B,④∠B-∠C=90°,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,3
8=24)
11.∠A=60°,∠B=30°,则△ABC是________三角形.
12.
如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,若∠B=35°,则∠1的度数是________.
13.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________________.
14.具备下列条件的△ABC:①∠A=∠B=∠C;②∠A=∠B=∠C;③∠A=∠C-∠B;④∠A-∠B=90°.其中不是直角三角形的是________(填序号).
15.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,CE是△ABC的角平分线.则∠DCE的度数是_________.
16.一个三角形的一个内角等于另外两个内角的和,这个三角形是________________.
17.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是( )
18.在△ABC中,∠A=48°,BD,CE是高,直线BD,CE交于点H,则∠BHC的度数是_________.
三.解答题(共7小题,
46分)
19.(6分)
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
20.(6分)
如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠EPF的度数.
21.(6分)
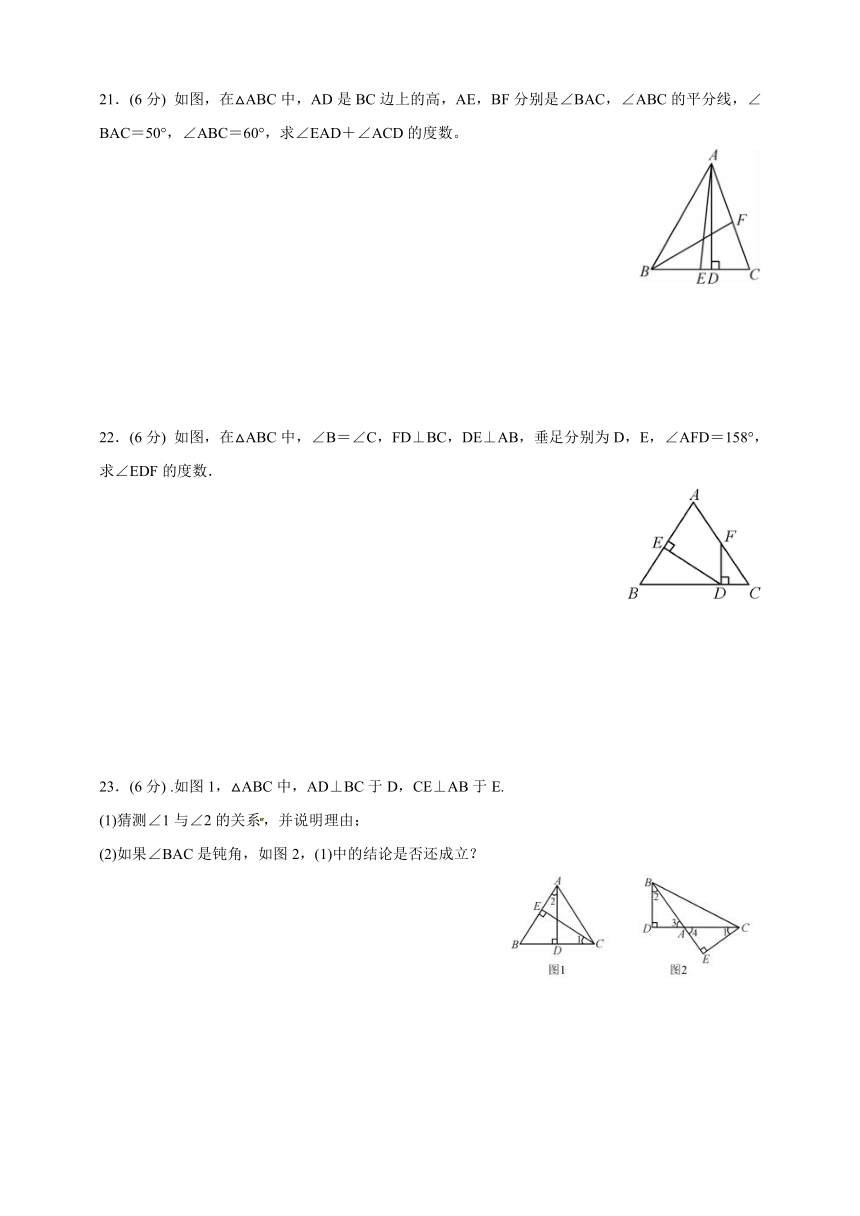
如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,求∠EAD+∠ACD的度数。
22.(6分)
如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.
23.(6分)
.如图1,△ABC中,AD⊥BC于D,CE⊥AB于E.
(1)猜测∠1与∠2的关系,并说明理由;
如果∠BAC是钝角,如图2,(1)中的结论是否还成立?
24.(8分)
(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.图中有与∠A相等的角吗?为什么?
(2)如图②,把图①中的D点向右移动,作ED⊥AB交BC于E,图中还有与∠A相等的角吗?为什么?
25.(8分)
如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:
(1)图中有几个直角三角形?
(2)∠AEH和∠B是什么关系?为什么?
(3)若∠B=70°,那么∠A和∠CED各是多少度?
参考答案
1-5
BBCCC
6-10DDDDC
11.
直角
12.
35°
13.
60°或10°
14.
④
15.
15°
16.直角三角形
17.20°
18.
132°或48°
19.
解:∵∠C=∠ABC=2∠A,
∴设∠A=x°,则∠ABC=∠C=2x°,
则x+2x+2x=180,∴x=36,
∴∠C=2x°=72°,
∵BD是高,∴∠DBC+∠C=90°,
∴∠DBC=90°-72°=18°
20.
解:∵∠FEP=90°,∠BEP=40°,
∴∠BEF=90°+40°=130°.
∵AB∥CD,∴∠EFD=180°-130°=50°.
∵FP平分∠EFD,∴∠EFP=25°.
∴∠EPF=90°-25°=65°.
21.
解:∵∠BAC=50°,∠ABC=60°,
∴∠ACD
=180°-50°-60°=70°.
∵∠BAC=50°,AE是∠BAC的平分线,
∴∠BAE=25°.
∵∠ABC=60°,
AD是BC边上的高,
∴∠BAD=30°.
∴∠EAD=∠BAD-∠BAE=5°.
∴∠EAD+∠ACD
=75°.
22.
解:∵∠AFD=158°,
∴∠DFC=180°-∠AFD=22°,
∵FD⊥BC,
∴∠FDC=90°,
∴∠DFC+∠C=90°,
∵DE⊥AB,
∴∠B+∠BDE=90°,
∵∠B=∠C,
∴∠BDE=∠DFC=22°,
∴∠EDF=180°-∠FDC-∠BDE=68°
23.
解:(1)∠1=∠2.理由如下:
∵AD⊥BC,CE⊥AB,∴△ABD和△BCE都是直角三角形,
∴∠1+∠B=90°,∠2+∠B=90°.
∴∠1=∠2.
(2)结论仍然成立.理由如下:
∵BD⊥AC,CE⊥AB,∴∠D=∠E=90°.
∴∠1+∠4=90°,∠2+∠3=90°.
∵∠3=∠4,∴∠1=∠2.
24.
(1)解:有.理由:因为CD⊥AB,
所以∠B+∠BCD=90°.
因为∠ACB=90°,
所以∠B+∠A=90°.
所以∠BCD=∠A.
(2)解:有.理由:因为ED⊥AB,
所以∠B+∠BED=90°.
因为∠ACB=90°,
所以∠B+∠A=90°.
所以∠BED=∠A.
25.
(1)解:∵DH⊥AB于H,
∴△AEH和△BDH都是直角三角形.
∵AC⊥BD于C,
∴△ABC和△CDE都是直角三角形,
∴图中有4个直角三角形.
(2)解:∠AEH=∠B.
理由:∵DH⊥AB,AC⊥BD,
∴∠AEH+∠A=90°,∠B+∠A=90°,
∴∠AEH=∠B.
(3)解:∵AC⊥BD,
∴∠ACB=90°,
∴∠A=90°-∠B=90°-70°=20°.
由(2)可知,∠AEH=∠B=70°,
∴∠CED=∠AEH=70°(对顶角相等).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
11.2.1.2直角三角形两锐角互余
能力提升卷
一、选择题(共10小题,3
10=30)
1.如图,AD是Rt△ABC的斜边BC上的高,则图中与∠B互余的角有( )
A.1个
B.2个
C.3个
D.4个
2.如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A.65°
B.70°
C.75°
D.85°
3.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E,若∠A=54°,∠B=48°,则∠CDE的度数为( )
A.44°
B.40°
C.39°
D.38°
4.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为(
)
A.50°
B.45°
C.40°
D.30°
5.如图,在Rt△ABC中,∠CAB=90°,∠ABC=72°,AD是∠CAB
的平分线,交边BC于点D,过点C作△ACD中AD
边上的高线CE,则∠ECD的度数为( )
A.63°
B.45°
C.27°
D.18°
6.
若一个三角形三个内角的度数之比为1∶2∶3,则这个三角形是( )
A.锐角三角形
B.等边三角形
C.钝角三角形
D.直角三角形
7.在△ABC中,∠A=∠B+∠C,∠B=2∠C-6°,则∠C的度数为( )
A.90°
B.58°
C.54°
D.32°
8.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A=∠B=∠C
C.∠A:∠B:∠C=1:3:4
D.∠A=2∠B=3∠C
9.如图,在△ABC中,∠ABC=62°,BD是角平分线,CE是高,BD与CE相交于点O,则∠BOC的度数是( )
A.118°
B.119°
C.120°
D.121°
10.在下列条件中:①∠A=∠C-∠B,②∠A∶∠B∶∠C=2∶3∶5,③∠A=90°-∠B,④∠B-∠C=90°,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,3
8=24)
11.∠A=60°,∠B=30°,则△ABC是________三角形.
12.
如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,若∠B=35°,则∠1的度数是________.
13.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为________________.
14.具备下列条件的△ABC:①∠A=∠B=∠C;②∠A=∠B=∠C;③∠A=∠C-∠B;④∠A-∠B=90°.其中不是直角三角形的是________(填序号).
15.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于点D,CE是△ABC的角平分线.则∠DCE的度数是_________.
16.一个三角形的一个内角等于另外两个内角的和,这个三角形是________________.
17.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是( )
18.在△ABC中,∠A=48°,BD,CE是高,直线BD,CE交于点H,则∠BHC的度数是_________.
三.解答题(共7小题,
46分)
19.(6分)
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
20.(6分)
如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠EPF的度数.
21.(6分)
如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线,∠BAC=50°,∠ABC=60°,求∠EAD+∠ACD的度数。
22.(6分)
如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.
23.(6分)
.如图1,△ABC中,AD⊥BC于D,CE⊥AB于E.
(1)猜测∠1与∠2的关系,并说明理由;
如果∠BAC是钝角,如图2,(1)中的结论是否还成立?
24.(8分)
(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB于D.图中有与∠A相等的角吗?为什么?
(2)如图②,把图①中的D点向右移动,作ED⊥AB交BC于E,图中还有与∠A相等的角吗?为什么?
25.(8分)
如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:
(1)图中有几个直角三角形?
(2)∠AEH和∠B是什么关系?为什么?
(3)若∠B=70°,那么∠A和∠CED各是多少度?
参考答案
1-5
BBCCC
6-10DDDDC
11.
直角
12.
35°
13.
60°或10°
14.
④
15.
15°
16.直角三角形
17.20°
18.
132°或48°
19.
解:∵∠C=∠ABC=2∠A,
∴设∠A=x°,则∠ABC=∠C=2x°,
则x+2x+2x=180,∴x=36,
∴∠C=2x°=72°,
∵BD是高,∴∠DBC+∠C=90°,
∴∠DBC=90°-72°=18°
20.
解:∵∠FEP=90°,∠BEP=40°,
∴∠BEF=90°+40°=130°.
∵AB∥CD,∴∠EFD=180°-130°=50°.
∵FP平分∠EFD,∴∠EFP=25°.
∴∠EPF=90°-25°=65°.
21.
解:∵∠BAC=50°,∠ABC=60°,
∴∠ACD
=180°-50°-60°=70°.
∵∠BAC=50°,AE是∠BAC的平分线,
∴∠BAE=25°.
∵∠ABC=60°,
AD是BC边上的高,
∴∠BAD=30°.
∴∠EAD=∠BAD-∠BAE=5°.
∴∠EAD+∠ACD
=75°.
22.
解:∵∠AFD=158°,
∴∠DFC=180°-∠AFD=22°,
∵FD⊥BC,
∴∠FDC=90°,
∴∠DFC+∠C=90°,
∵DE⊥AB,
∴∠B+∠BDE=90°,
∵∠B=∠C,
∴∠BDE=∠DFC=22°,
∴∠EDF=180°-∠FDC-∠BDE=68°
23.
解:(1)∠1=∠2.理由如下:
∵AD⊥BC,CE⊥AB,∴△ABD和△BCE都是直角三角形,
∴∠1+∠B=90°,∠2+∠B=90°.
∴∠1=∠2.
(2)结论仍然成立.理由如下:
∵BD⊥AC,CE⊥AB,∴∠D=∠E=90°.
∴∠1+∠4=90°,∠2+∠3=90°.
∵∠3=∠4,∴∠1=∠2.
24.
(1)解:有.理由:因为CD⊥AB,
所以∠B+∠BCD=90°.
因为∠ACB=90°,
所以∠B+∠A=90°.
所以∠BCD=∠A.
(2)解:有.理由:因为ED⊥AB,
所以∠B+∠BED=90°.
因为∠ACB=90°,
所以∠B+∠A=90°.
所以∠BED=∠A.
25.
(1)解:∵DH⊥AB于H,
∴△AEH和△BDH都是直角三角形.
∵AC⊥BD于C,
∴△ABC和△CDE都是直角三角形,
∴图中有4个直角三角形.
(2)解:∠AEH=∠B.
理由:∵DH⊥AB,AC⊥BD,
∴∠AEH+∠A=90°,∠B+∠A=90°,
∴∠AEH=∠B.
(3)解:∵AC⊥BD,
∴∠ACB=90°,
∴∠A=90°-∠B=90°-70°=20°.
由(2)可知,∠AEH=∠B=70°,
∴∠CED=∠AEH=70°(对顶角相等).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
