人教版八年级数学下册第十八章平行四边形综合培优训练(word、含答案)
文档属性
| 名称 | 人教版八年级数学下册第十八章平行四边形综合培优训练(word、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 178.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 21:52:44 | ||
图片预览


文档简介
第18章
《平行四边形》单元检测卷
一.选择题
1.若菱形的周长为16,高为2,则菱形两邻角的度数之比为( )
A.4:1
B.5:1
C.6:1
D.7:1
2.已知△ABC的周长为16,点D,E,F分别为△ABC三条边的中点,则△DEF的周长为( )
A.8
B.2
C.16
D.4
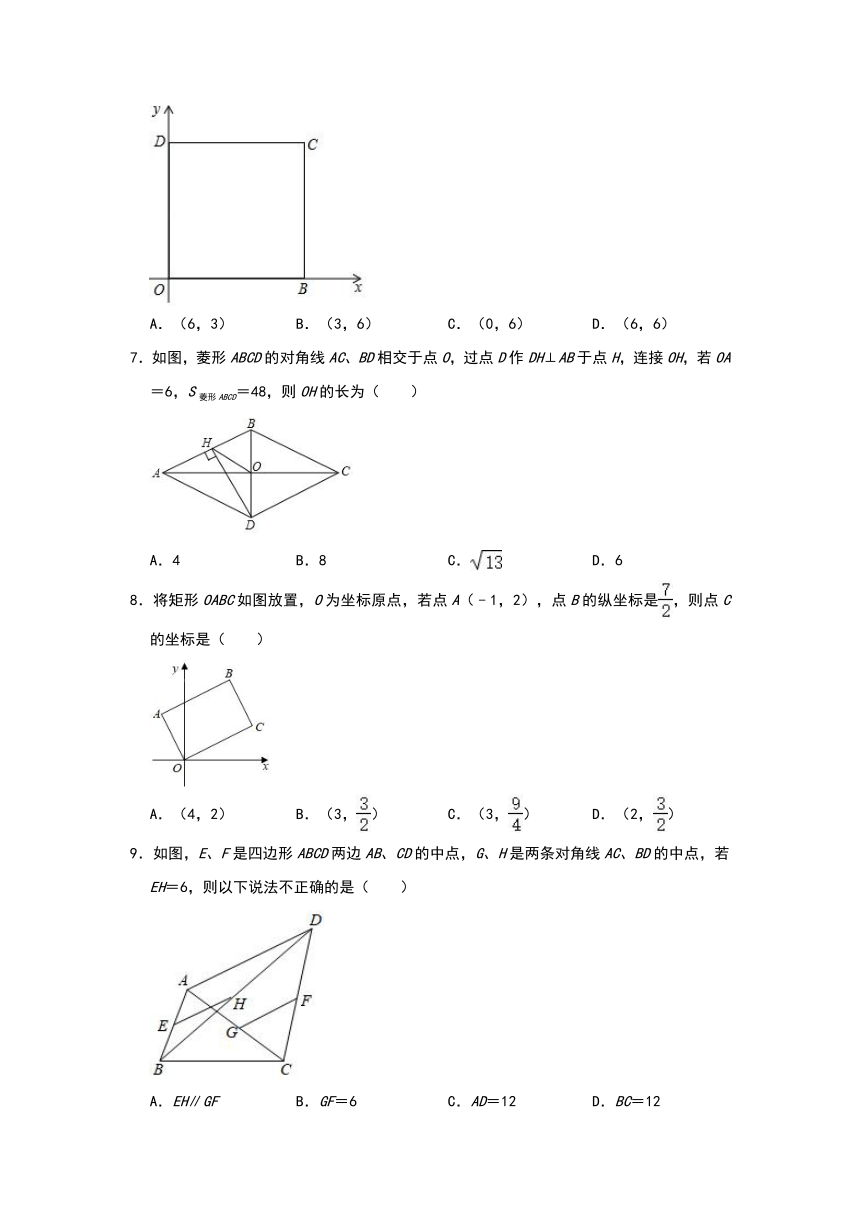
3.如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为( )
A.
B.
C.3
D.5
4.如图,在矩形ABCD中,AD=3AB,且AB=2,点G、H分别在AD、BC上,连接BG、DH,若四边形BHDG是菱形,则AG的长为( )
A.
B.3
C.
D.4
5.如图所示,?ABCD中,AC的垂直平分线交于点E,且△CDE的周长为8,则?ABCD的周长是( )
A.10
B.12
C.14
D.16
6.如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3)
B.(3,6)
C.(0,6)
D.(6,6)
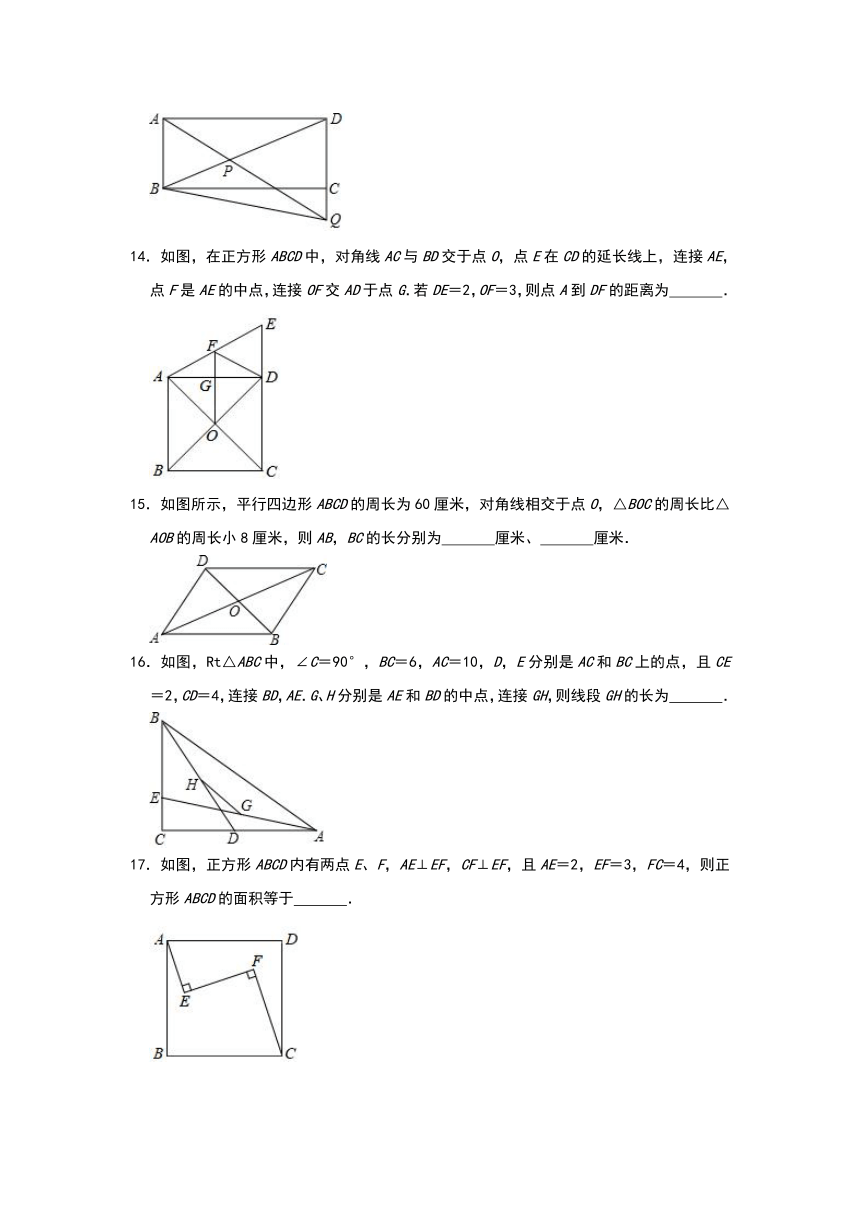
7.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为( )
A.4
B.8
C.
D.6
8.将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是,则点C的坐标是( )
A.(4,2)
B.(3,)
C.(3,)
D.(2,)
9.如图,E、F是四边形ABCD两边AB、CD的中点,G、H是两条对角线AC、BD的中点,若EH=6,则以下说法不正确的是( )
A.EH∥GF
B.GF=6
C.AD=12
D.BC=12
10.如图,在Rt△ABC中,CD为斜边AB的中线,过点D作DE⊥AC于点E,延长DE至点F,使EF=DE,连接AF,CF,点G在线段CF上,连接EG,且∠CDE+∠EGC=180°,FG=2,GC=3.下列结论:
①DE=BC;
②四边形DBCF是平行四边形;
③EF=EG;
④BC=2.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
二.填空题
11.如图,在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=3cm,则AC的长为
cm.
12.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE=
.
13.如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP并延长,交DC的延长线于点Q,连接BQ,则BQ的长为
.
14.如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为
.
15.如图所示,平行四边形ABCD的周长为60厘米,对角线相交于点O,△BOC的周长比△AOB的周长小8厘米,则AB,BC的长分别为
厘米、
厘米.
16.如图,Rt△ABC中,∠C=90°,BC=6,AC=10,D,E分别是AC和BC上的点,且CE=2,CD=4,连接BD,AE.G、H分别是AE和BD的中点,连接GH,则线段GH的长为
.
17.如图,正方形ABCD内有两点E、F,AE⊥EF,CF⊥EF,且AE=2,EF=3,FC=4,则正方形ABCD的面积等于
.
三.解答题
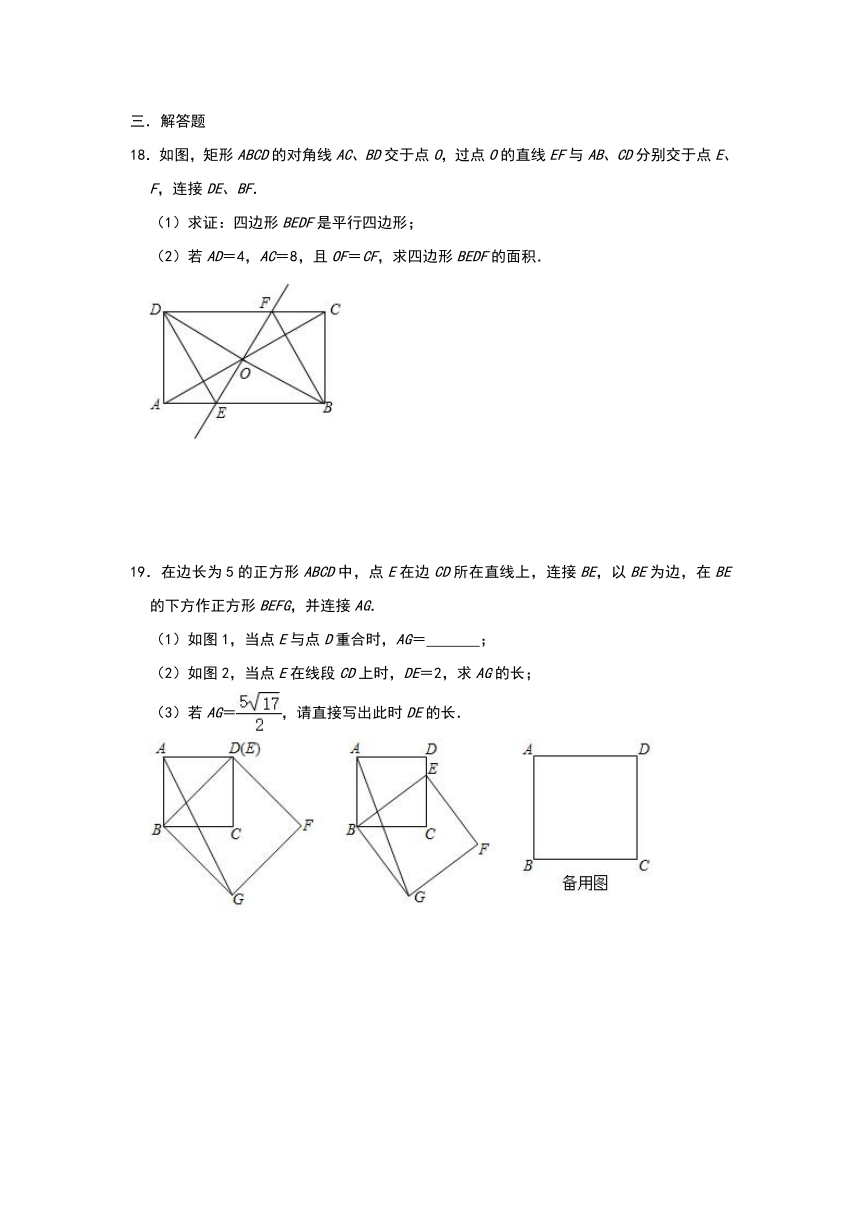
18.如图,矩形ABCD的对角线AC、BD交于点O,过点O的直线EF与AB、CD分别交于点E、F,连接DE、BF.
(1)求证:四边形BEDF是平行四边形;
(2)若AD=4,AC=8,且OF=CF,求四边形BEDF的面积.
19.在边长为5的正方形ABCD中,点E在边CD所在直线上,连接BE,以BE为边,在BE的下方作正方形BEFG,并连接AG.
(1)如图1,当点E与点D重合时,AG=
;
(2)如图2,当点E在线段CD上时,DE=2,求AG的长;
(3)若AG=,请直接写出此时DE的长.
20.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.
(1)求∠BGC的度数;
(2)若CE=1,H为BF的中点时,求HG的长度;
(3)若图中阴影部分的面积与正方形ABCD的面积之比为2:3,求△BCG的周长.
参考答案
一.选择题
1.
B.2.
A.3.
B.4.
A.5.
D.6.
D.7.
A.8.
B.9.
D.10.
D.
二.填空题
11.
6
12.
5.
13.
3.
14.
.
15.
19,11.
16.
.
17.
.
三.解答题
18.解:(1)在矩形ABCD中,
OB=OD,CD∥AB,
∴∠FDO=∠EBO,
在△OFD与△OEB中,
,
∴△OFD≌△OEB(AAS),
∴OF=OE,
∵OB=OD,
∴四边形BEDF是平行四边形.
(2)在矩形ABCD中,
AD=4,AC=8,
∴AD=OA=OD=4,
∴△AOD是等边三角形,
∴∠DCA=30°,∠DOA=60°,
∵OF=CF,
∴∠FOC=∠FCO=30°,
∴∠DOF=90°,
∴四边形BEDF是菱形,
在Rt△DOF中,
∠FDO=30°,OD=4,
∴OF=,
∵AC=BD=8,
∴菱形BEDF的面积为:BD?2OF=BD?OF=
19.解:(1)如图1,连接CG,
∵四边形ABCD和四边形EBGF是正方形,
∴∠CDB=∠CBD=45°,∠DBG=90°,BD=BG,
∴∠CBG=45°,
∴∠CBG=∠CBD,
∵BC=BC,
∴△CBD≌△CBG(SAS),
∴∠DCB=∠BCG=90°,DC=CG=5,
∴G,C,D三点共线,
∴AG===5;
故答案为:5;
(2)如图2,过点G作GK⊥AB,交AB的延长线于K,
∵DE=2,DC=5,
∴CE=3,
∵∠EBG=∠EBC+∠CBG=90°,∠CBG+∠GBK=90°,
∴∠EBC=∠GBK,
∵BE=BG,∠K=∠BCE=90°,
∴△BCE≌△BKG(AAS),
∴CE=KG=3,BC=BK=5,
∴AK=10,
由勾股定理得:AG==;
(3)分三种情况:
①当点E在CD的延长线上时,如图3,同理知△BCE≌△BKG(AAS),
∴BC=BK=5,
∵AG=,
由勾股定理得:KG==,
∴CE=KG=,此种情况不成立;
②当点E在边CD上时,如图4,
同理得:DE=;
③当点E在DC的延长线上时,如图5,
同理得CE=GK=,
∴DE=5+=,
综上,DE的长是或.
20.解:(1)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠CDF=90°,
在△BCE和△CDF中,∵BC=CD,∠BCD=∠CDF,CE=DF,
∴△BCE≌△CDF(SAS),
∴∠CBE=∠DCF,
又∵∠BCG+∠DCF=90°,
∴∠BCG+∠CBE=90°,
∴∠BGC=90°;
(2)如图,∵CE=1,
∴DF=1,
∴AF=2,
在直角△ABF中,由勾股定理得:,
∵H为BF的中点,∠BGF=90°,
∴;
(3)∵阴影部分的面积与正方形ABCD的面积之比为2:3,
∴阴影部分的面积为×9=6,
∴空白部分的面积为9﹣6=3,
∵△BCE≌△CDF,
∴△BCG的面积与四边形DEGF的面积相等,均为×3=,
设BG=a,CG=b,则ab=,
∴ab=3,
又∵a2+b2=32,
∴a2+2ab+b2=9+6=15,
即(a+b)2=15,
∴a+b=,即BG+CG=,
∴△BCG的周长=+3.
《平行四边形》单元检测卷
一.选择题
1.若菱形的周长为16,高为2,则菱形两邻角的度数之比为( )
A.4:1
B.5:1
C.6:1
D.7:1
2.已知△ABC的周长为16,点D,E,F分别为△ABC三条边的中点,则△DEF的周长为( )
A.8
B.2
C.16
D.4
3.如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为( )
A.
B.
C.3
D.5
4.如图,在矩形ABCD中,AD=3AB,且AB=2,点G、H分别在AD、BC上,连接BG、DH,若四边形BHDG是菱形,则AG的长为( )
A.
B.3
C.
D.4
5.如图所示,?ABCD中,AC的垂直平分线交于点E,且△CDE的周长为8,则?ABCD的周长是( )
A.10
B.12
C.14
D.16
6.如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3)
B.(3,6)
C.(0,6)
D.(6,6)
7.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为( )
A.4
B.8
C.
D.6
8.将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是,则点C的坐标是( )
A.(4,2)
B.(3,)
C.(3,)
D.(2,)
9.如图,E、F是四边形ABCD两边AB、CD的中点,G、H是两条对角线AC、BD的中点,若EH=6,则以下说法不正确的是( )
A.EH∥GF
B.GF=6
C.AD=12
D.BC=12
10.如图,在Rt△ABC中,CD为斜边AB的中线,过点D作DE⊥AC于点E,延长DE至点F,使EF=DE,连接AF,CF,点G在线段CF上,连接EG,且∠CDE+∠EGC=180°,FG=2,GC=3.下列结论:
①DE=BC;
②四边形DBCF是平行四边形;
③EF=EG;
④BC=2.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
二.填空题
11.如图,在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=3cm,则AC的长为
cm.
12.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE=
.
13.如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP并延长,交DC的延长线于点Q,连接BQ,则BQ的长为
.
14.如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为
.
15.如图所示,平行四边形ABCD的周长为60厘米,对角线相交于点O,△BOC的周长比△AOB的周长小8厘米,则AB,BC的长分别为
厘米、
厘米.
16.如图,Rt△ABC中,∠C=90°,BC=6,AC=10,D,E分别是AC和BC上的点,且CE=2,CD=4,连接BD,AE.G、H分别是AE和BD的中点,连接GH,则线段GH的长为
.
17.如图,正方形ABCD内有两点E、F,AE⊥EF,CF⊥EF,且AE=2,EF=3,FC=4,则正方形ABCD的面积等于
.
三.解答题
18.如图,矩形ABCD的对角线AC、BD交于点O,过点O的直线EF与AB、CD分别交于点E、F,连接DE、BF.
(1)求证:四边形BEDF是平行四边形;
(2)若AD=4,AC=8,且OF=CF,求四边形BEDF的面积.
19.在边长为5的正方形ABCD中,点E在边CD所在直线上,连接BE,以BE为边,在BE的下方作正方形BEFG,并连接AG.
(1)如图1,当点E与点D重合时,AG=
;
(2)如图2,当点E在线段CD上时,DE=2,求AG的长;
(3)若AG=,请直接写出此时DE的长.
20.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.
(1)求∠BGC的度数;
(2)若CE=1,H为BF的中点时,求HG的长度;
(3)若图中阴影部分的面积与正方形ABCD的面积之比为2:3,求△BCG的周长.
参考答案
一.选择题
1.
B.2.
A.3.
B.4.
A.5.
D.6.
D.7.
A.8.
B.9.
D.10.
D.
二.填空题
11.
6
12.
5.
13.
3.
14.
.
15.
19,11.
16.
.
17.
.
三.解答题
18.解:(1)在矩形ABCD中,
OB=OD,CD∥AB,
∴∠FDO=∠EBO,
在△OFD与△OEB中,
,
∴△OFD≌△OEB(AAS),
∴OF=OE,
∵OB=OD,
∴四边形BEDF是平行四边形.
(2)在矩形ABCD中,
AD=4,AC=8,
∴AD=OA=OD=4,
∴△AOD是等边三角形,
∴∠DCA=30°,∠DOA=60°,
∵OF=CF,
∴∠FOC=∠FCO=30°,
∴∠DOF=90°,
∴四边形BEDF是菱形,
在Rt△DOF中,
∠FDO=30°,OD=4,
∴OF=,
∵AC=BD=8,
∴菱形BEDF的面积为:BD?2OF=BD?OF=
19.解:(1)如图1,连接CG,
∵四边形ABCD和四边形EBGF是正方形,
∴∠CDB=∠CBD=45°,∠DBG=90°,BD=BG,
∴∠CBG=45°,
∴∠CBG=∠CBD,
∵BC=BC,
∴△CBD≌△CBG(SAS),
∴∠DCB=∠BCG=90°,DC=CG=5,
∴G,C,D三点共线,
∴AG===5;
故答案为:5;
(2)如图2,过点G作GK⊥AB,交AB的延长线于K,
∵DE=2,DC=5,
∴CE=3,
∵∠EBG=∠EBC+∠CBG=90°,∠CBG+∠GBK=90°,
∴∠EBC=∠GBK,
∵BE=BG,∠K=∠BCE=90°,
∴△BCE≌△BKG(AAS),
∴CE=KG=3,BC=BK=5,
∴AK=10,
由勾股定理得:AG==;
(3)分三种情况:
①当点E在CD的延长线上时,如图3,同理知△BCE≌△BKG(AAS),
∴BC=BK=5,
∵AG=,
由勾股定理得:KG==,
∴CE=KG=,此种情况不成立;
②当点E在边CD上时,如图4,
同理得:DE=;
③当点E在DC的延长线上时,如图5,
同理得CE=GK=,
∴DE=5+=,
综上,DE的长是或.
20.解:(1)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠CDF=90°,
在△BCE和△CDF中,∵BC=CD,∠BCD=∠CDF,CE=DF,
∴△BCE≌△CDF(SAS),
∴∠CBE=∠DCF,
又∵∠BCG+∠DCF=90°,
∴∠BCG+∠CBE=90°,
∴∠BGC=90°;
(2)如图,∵CE=1,
∴DF=1,
∴AF=2,
在直角△ABF中,由勾股定理得:,
∵H为BF的中点,∠BGF=90°,
∴;
(3)∵阴影部分的面积与正方形ABCD的面积之比为2:3,
∴阴影部分的面积为×9=6,
∴空白部分的面积为9﹣6=3,
∵△BCE≌△CDF,
∴△BCG的面积与四边形DEGF的面积相等,均为×3=,
设BG=a,CG=b,则ab=,
∴ab=3,
又∵a2+b2=32,
∴a2+2ab+b2=9+6=15,
即(a+b)2=15,
∴a+b=,即BG+CG=,
∴△BCG的周长=+3.
