人教版八年级上册:11.1.1 三角形的边 讲义(知识点+练习)(无答案)
文档属性
| 名称 | 人教版八年级上册:11.1.1 三角形的边 讲义(知识点+练习)(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 200.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 11:35:00 | ||
图片预览


文档简介
三角形的边
三角形的定义:由不在同一直线的三条线段首尾顺次相连组成的图形,叫做三角形。
三角形的表示:记作△ABC
顶点:点A、点B、点C
边:AB、AC、BC或a、b、c
角:∠A(∠BAC)、∠B(∠ABC)、∠C(∠ACB)
例1.如图所示.
图中共有多少个三角形?并把它们写出来;
线段AE是哪些三角形的边?
(3)∠B是哪些三角形的角?
练习:如图所示,
图中共有______个三角形,其中以线段BC为一边的三角形是______,
以∠EAD为一内角的三角形是__________.
(2)在△ABD中,∠BAD的对边是______,在△ABE中,∠ABE的对边是______.
(3)AB既是△______中∠______的对边,又是△______中∠______的对边,还是△______中∠______的对边。
三角形的分类:
按角分:
按边分
注意:
①等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角;
②等边三角形:三边都相等的三角形.
例2.已知(a-b)2+|b-c|=0,若a、b、c为△ABC的三边,那么△ABC是什么三角形?
三角形的三边关系:
由“两点之间线段最短”可得
AB+AC>BC
同理可得
AB+BC>AC,BC+AC>AB
即三角形的两边之和大于第三边。
将不等式移项得AB>BC-AC
,BC>AC-AB,AC>AB-BC
即三角形的两边之差小于第三边。
【例3--1】.判断下列三条线段能否构成三角形.
(1)
3,4,5;
(2)
3,5,9
;
(3)
5,5,8;
(4)4,6,7
【例3--2】.若三角形的两边长分别是2和7,则第三边长c的取值范围是_____________.
【例3--3】.设a,b,c是三角形三边,化简:|a-b+c|-|a-b-c|+|-c+b-a|
【例3--4】三角形三边为3,5,3-4a,则a的范围是
。
【例3--5】.已知△ABC是等腰三角形,
(1)若周长是20,一边长是8,求另两边长;
(2)若周长是20,一边长是5,求另两边长.
练习:1.若三角形两条边长分别为6cm和4cm,且第三边长为偶数,则该三角形的周长为______cm。
以下列各组线段的长为边长,能组成三角形的是(
)
A.2,3,5
B.3,4,5
C.3,5,10
D.4,4,8
3.已知等腰三角形的两边长分别是5和6,则这个等腰三角形的周长为(
)
A.11
B.16
C.17
D.16或17
4.若a,b,c分别是三角形三边,化简:|a-b-c|+|b-c-a|+|c-a+b|
已知,a、b、c为△ABC的三边长,b、c满足(b?2)2+|c?3|=0,且a为方程|a?4|=2的解,求△ABC的周长,并判断△ABC的形状。
三角形中的三条重要线段:高,中线,角平分线
三角形的高
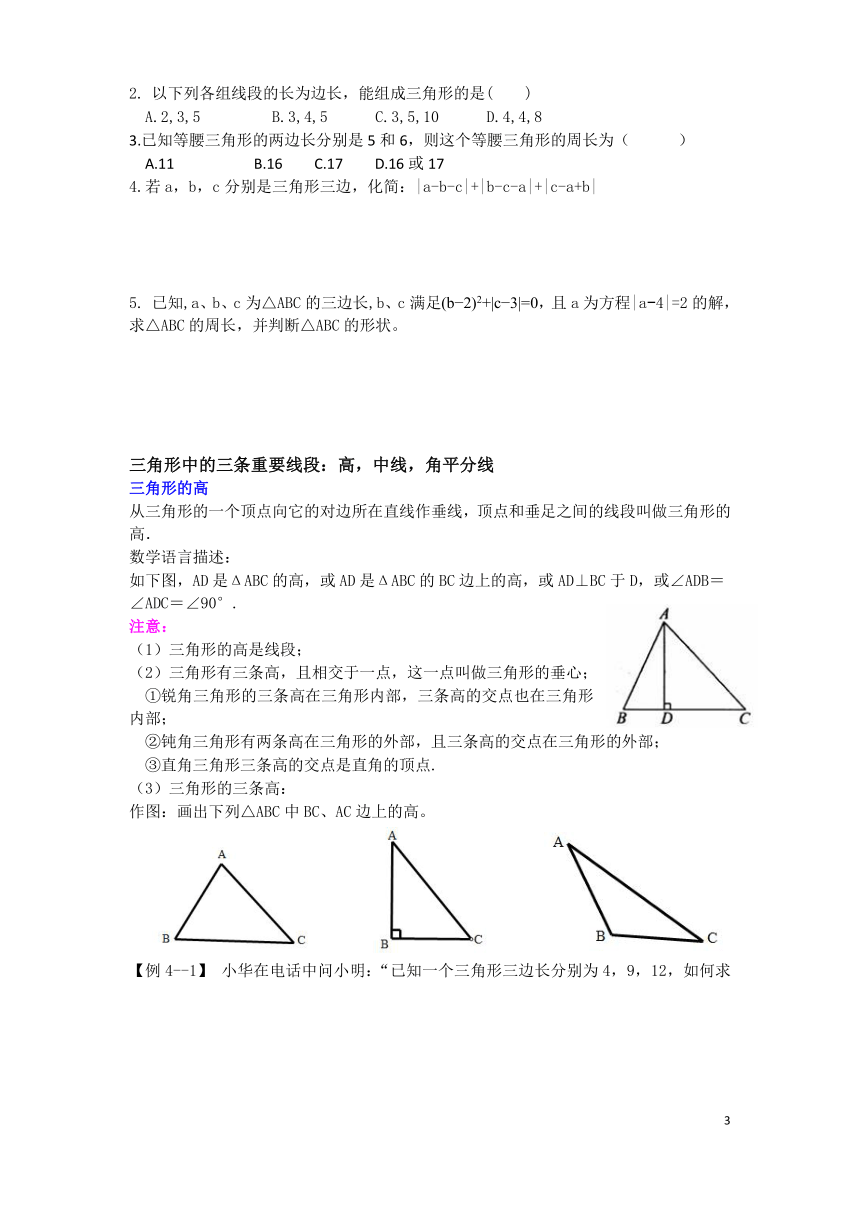
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高.
数学语言描述:
如下图,AD是ΔABC的高,或AD是ΔABC的BC边上的高,或AD⊥BC于D,或∠ADB=∠ADC=∠90°.
注意:
(1)三角形的高是线段;
(2)三角形有三条高,且相交于一点,这一点叫做三角形的垂心;
①锐角三角形的三条高在三角形内部,三条高的交点也在三角形内部;
②钝角三角形有两条高在三角形的外部,且三条高的交点在三角形的外部;
③直角三角形三条高的交点是直角的顶点.
(3)三角形的三条高:
作图:画出下列△ABC中BC、AC边上的高。
【例4--1】
小华在电话中问小明:“已知一个三角形三边长分别为4,9,12,如何求这个三角形的面积?”小明提示:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是(
)
【变式】如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
B.
C.
D.
【例4--2】.如图,在直角三角形ABC中,AB=13,AC=12,BC=5,求△ABC的面积,以及AB边上的高CD的长。
练习:如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
(1)求△ABC的面积;
(2)求BC的长。
三角形的中线
三角形的一个顶点与它的对边中点的连线叫三角形的中线.
注意:(1)三角形的中线是线段;
(2)三角形三条中线全在三角形内部;
(3)三角形三条中线交于三角形内部一点,这一点叫三角形的重心;
(4)中线把三角形分成面积相等的两个三角形.
【例4--3】.如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.
练习:在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长。
【例4--4】.如图1,AB⊥BD于点B,AC⊥CD于点C,且AC与BD相交于点E,则△ADE的边DE上高是______;边AE上的高为_______;若AE=5,ED=2,CD=,则AB=_______.
【例4--5】.如图2,AD,AE分别为△ABC的中线和角平分线,已知BC=10cm,∠BAC=70°,则BD=______=______??=______cm,∠BAE=?______=______=______.若△ABD的周长比△ACD的周长多3cm,则AB-AC=_______cm.
图1
图2
图3
图4
练习:(1)如图3所示,在△ABC中,D、E分别为BC、AD的中点,且,则为________.
(2)如图4,若AD、AE分别是△ABC的高和中线,AD=BE=2,则△ABE的面积为______.
(3)李爷爷家有一块三角形的花圃,他准备将其分成面积相等的四个部分,分别种上四种不同的花,请你帮李爷爷设计两种方案。
三角形的角平分线
三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形的角平分线的数学语言:
如下图,AD是ΔABC的角平分线,或∠BAD=∠CAD且点D在BC上.
注意:(1)三角形的角平分线是线段;
(2)一个三角形有三条角平分线,并且都在三角形的内部;
(3)三角形三条角平分线交于三角形内部一点,这一点叫做三角形的内心;
(4)可以用量角器或圆规画三角形的角平分线.
三角形的稳定性
三角形的三边长一旦确定,三角形的形状就唯一确定,这个性质叫做三角形的稳定性。四边形则不具有稳定性。
钢架桥、屋顶钢架和起重机都是利用三角形的稳定性,伸缩门则是利用四边形的不稳定性。你还能举出一些例子吗?
作业1:
1.如图1,在ΔABC中,D,E分别为BC,AD的中点,且SΔABC=4,则S阴影为(
)
A.2
B.1
C.
D.
2.长为9,6,5,4的四根木条,选其中三根组成一个三角形,选法有(
)
A.1种
B.2种
C.3种
D.4种
3.如图2,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D.
C.?F,下列说法中,错误的是(
)
A.△ABC中,AD是边BC上的高
B.△ABC中,GC是边BC上的高
C.△GBC中,GC是边BC上的高
D.△GBC中,CF是边BG上的高
4.如图3,若∠1=∠2,∠3=∠4,下列结论中错误的是(
)
A.AD是△ABC的角平分线
B.CE是△ACD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
5.如图4,△ABC中,∠A=80゜,高BE和CH的交点为O,则∠BOC等于(
?)
A.?80゜
B.?120゜
C.?100゜
D.?150゜
图1
图2
图3
图4
图5
6.如图5,图中有____个三角形,它们分别是___________;∠B是_____的内角;在△ABE中,BE边所对的角是______,∠B所对的边是______;在△ADE中,AD是______对的边;在△ADC中,AD是______的对边。
7.如图,已知△ABC,按下列要求作图:
(1)画出∠ABC的平分线,并指出相等的角;
(2)画出AC边上的中线,并指出相等的线段;
(3)画出BC边上的高,并指出图中所有的直角三角形.
8.若一个等腰三角形的两条边长分别是7cm和14cm,则它的周长是_______。
9.在△ABC中,AB=AC,AD是中线,△ABC的周长为34cm,△ABD的周长为30cm,求AD的长。
10.已知实数x,y满足|x-5|+=0,求以x,y的值为两边长的等腰三角形的周长。
三角形的定义:由不在同一直线的三条线段首尾顺次相连组成的图形,叫做三角形。
三角形的表示:记作△ABC
顶点:点A、点B、点C
边:AB、AC、BC或a、b、c
角:∠A(∠BAC)、∠B(∠ABC)、∠C(∠ACB)
例1.如图所示.
图中共有多少个三角形?并把它们写出来;
线段AE是哪些三角形的边?
(3)∠B是哪些三角形的角?
练习:如图所示,
图中共有______个三角形,其中以线段BC为一边的三角形是______,
以∠EAD为一内角的三角形是__________.
(2)在△ABD中,∠BAD的对边是______,在△ABE中,∠ABE的对边是______.
(3)AB既是△______中∠______的对边,又是△______中∠______的对边,还是△______中∠______的对边。
三角形的分类:
按角分:
按边分
注意:
①等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角;
②等边三角形:三边都相等的三角形.
例2.已知(a-b)2+|b-c|=0,若a、b、c为△ABC的三边,那么△ABC是什么三角形?
三角形的三边关系:
由“两点之间线段最短”可得
AB+AC>BC
同理可得
AB+BC>AC,BC+AC>AB
即三角形的两边之和大于第三边。
将不等式移项得AB>BC-AC
,BC>AC-AB,AC>AB-BC
即三角形的两边之差小于第三边。
【例3--1】.判断下列三条线段能否构成三角形.
(1)
3,4,5;
(2)
3,5,9
;
(3)
5,5,8;
(4)4,6,7
【例3--2】.若三角形的两边长分别是2和7,则第三边长c的取值范围是_____________.
【例3--3】.设a,b,c是三角形三边,化简:|a-b+c|-|a-b-c|+|-c+b-a|
【例3--4】三角形三边为3,5,3-4a,则a的范围是
。
【例3--5】.已知△ABC是等腰三角形,
(1)若周长是20,一边长是8,求另两边长;
(2)若周长是20,一边长是5,求另两边长.
练习:1.若三角形两条边长分别为6cm和4cm,且第三边长为偶数,则该三角形的周长为______cm。
以下列各组线段的长为边长,能组成三角形的是(
)
A.2,3,5
B.3,4,5
C.3,5,10
D.4,4,8
3.已知等腰三角形的两边长分别是5和6,则这个等腰三角形的周长为(
)
A.11
B.16
C.17
D.16或17
4.若a,b,c分别是三角形三边,化简:|a-b-c|+|b-c-a|+|c-a+b|
已知,a、b、c为△ABC的三边长,b、c满足(b?2)2+|c?3|=0,且a为方程|a?4|=2的解,求△ABC的周长,并判断△ABC的形状。
三角形中的三条重要线段:高,中线,角平分线
三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高.
数学语言描述:
如下图,AD是ΔABC的高,或AD是ΔABC的BC边上的高,或AD⊥BC于D,或∠ADB=∠ADC=∠90°.
注意:
(1)三角形的高是线段;
(2)三角形有三条高,且相交于一点,这一点叫做三角形的垂心;
①锐角三角形的三条高在三角形内部,三条高的交点也在三角形内部;
②钝角三角形有两条高在三角形的外部,且三条高的交点在三角形的外部;
③直角三角形三条高的交点是直角的顶点.
(3)三角形的三条高:
作图:画出下列△ABC中BC、AC边上的高。
【例4--1】
小华在电话中问小明:“已知一个三角形三边长分别为4,9,12,如何求这个三角形的面积?”小明提示:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是(
)
【变式】如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
B.
C.
D.
【例4--2】.如图,在直角三角形ABC中,AB=13,AC=12,BC=5,求△ABC的面积,以及AB边上的高CD的长。
练习:如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
(1)求△ABC的面积;
(2)求BC的长。
三角形的中线
三角形的一个顶点与它的对边中点的连线叫三角形的中线.
注意:(1)三角形的中线是线段;
(2)三角形三条中线全在三角形内部;
(3)三角形三条中线交于三角形内部一点,这一点叫三角形的重心;
(4)中线把三角形分成面积相等的两个三角形.
【例4--3】.如图所示,CD为△ABC的AB边上的中线,△BCD的周长比△ACD的周长大3cm,BC=8cm,求边AC的长.
练习:在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长。
【例4--4】.如图1,AB⊥BD于点B,AC⊥CD于点C,且AC与BD相交于点E,则△ADE的边DE上高是______;边AE上的高为_______;若AE=5,ED=2,CD=,则AB=_______.
【例4--5】.如图2,AD,AE分别为△ABC的中线和角平分线,已知BC=10cm,∠BAC=70°,则BD=______=______??=______cm,∠BAE=?______=______=______.若△ABD的周长比△ACD的周长多3cm,则AB-AC=_______cm.
图1
图2
图3
图4
练习:(1)如图3所示,在△ABC中,D、E分别为BC、AD的中点,且,则为________.
(2)如图4,若AD、AE分别是△ABC的高和中线,AD=BE=2,则△ABE的面积为______.
(3)李爷爷家有一块三角形的花圃,他准备将其分成面积相等的四个部分,分别种上四种不同的花,请你帮李爷爷设计两种方案。
三角形的角平分线
三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形的角平分线的数学语言:
如下图,AD是ΔABC的角平分线,或∠BAD=∠CAD且点D在BC上.
注意:(1)三角形的角平分线是线段;
(2)一个三角形有三条角平分线,并且都在三角形的内部;
(3)三角形三条角平分线交于三角形内部一点,这一点叫做三角形的内心;
(4)可以用量角器或圆规画三角形的角平分线.
三角形的稳定性
三角形的三边长一旦确定,三角形的形状就唯一确定,这个性质叫做三角形的稳定性。四边形则不具有稳定性。
钢架桥、屋顶钢架和起重机都是利用三角形的稳定性,伸缩门则是利用四边形的不稳定性。你还能举出一些例子吗?
作业1:
1.如图1,在ΔABC中,D,E分别为BC,AD的中点,且SΔABC=4,则S阴影为(
)
A.2
B.1
C.
D.
2.长为9,6,5,4的四根木条,选其中三根组成一个三角形,选法有(
)
A.1种
B.2种
C.3种
D.4种
3.如图2,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D.
C.?F,下列说法中,错误的是(
)
A.△ABC中,AD是边BC上的高
B.△ABC中,GC是边BC上的高
C.△GBC中,GC是边BC上的高
D.△GBC中,CF是边BG上的高
4.如图3,若∠1=∠2,∠3=∠4,下列结论中错误的是(
)
A.AD是△ABC的角平分线
B.CE是△ACD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
5.如图4,△ABC中,∠A=80゜,高BE和CH的交点为O,则∠BOC等于(
?)
A.?80゜
B.?120゜
C.?100゜
D.?150゜
图1
图2
图3
图4
图5
6.如图5,图中有____个三角形,它们分别是___________;∠B是_____的内角;在△ABE中,BE边所对的角是______,∠B所对的边是______;在△ADE中,AD是______对的边;在△ADC中,AD是______的对边。
7.如图,已知△ABC,按下列要求作图:
(1)画出∠ABC的平分线,并指出相等的角;
(2)画出AC边上的中线,并指出相等的线段;
(3)画出BC边上的高,并指出图中所有的直角三角形.
8.若一个等腰三角形的两条边长分别是7cm和14cm,则它的周长是_______。
9.在△ABC中,AB=AC,AD是中线,△ABC的周长为34cm,△ABD的周长为30cm,求AD的长。
10.已知实数x,y满足|x-5|+=0,求以x,y的值为两边长的等腰三角形的周长。
