人教版八年级上册:11.2 与三角形有关的角 讲义(知识点+练习)(无答案)
文档属性
| 名称 | 人教版八年级上册:11.2 与三角形有关的角 讲义(知识点+练习)(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
图片预览


文档简介
第2讲
与三角形有关的角
三角形内角和定理
(1)定理:三角形三个内角的和等于180°.
(2)证明方法:证法多样,主要是运用平行线知识把三个角转移成一个平角,从而得到内角和是180°。
①如图所示,过C作CM∥AB,将求∠A+∠B+∠ACB转化为求∠1+∠2+∠ACB,
②过A点作DE∥BC,把求∠BAC+∠B+∠C转化为求∠BAC+∠DAB+∠EAC.
理解与延伸:①一个三角形中最多只有一个钝角或直角;
②一个三角形中最少有一个角不小于60°;
③直角三角形两锐角互余;
④等边三角形每个角都是60°.
(4)作用:求角度,尤其是三角形中的角度计算。
【例1-1】
填空:
(1)在△ABC中,若∠A=80°,∠C=20°,则∠B=__________°;
(2)若∠A=80°,∠B=∠C,则∠C=__________°;
(3)已知△ABC的三个内角的度数之比∠A∶∠B∶∠C=2∶3∶5,则∠B=________°,∠C=_________°.
【例1-2】如图,在△ABC中,∠CAB=∠B=2∠C,AD是∠BAC的平分线,求∠ADC的度数.
【例1-3】如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数。
【例1-4】若等腰三角形的一内角为40°,则顶角为(
)
40°
B.
100°
C.
70°或40°
D.40°或100°
直角三角形的性质与判定
(1)直角三角形的性质:直角三角形的两个锐角互余.
如图所示,在Rt△ABC中,如果∠C=90°,那么∠A+∠B=90°.
【例2-1】
将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是
( ).
A.43°
B.47°
C.30°
D.60°
【例2-2】
如图所示,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,求证:△EPF是直角三角形.
判定:有两个角互余的三角形是直角三角形。
【例2-3】下列条件能确定△ABC是直角三角形的条件有_____________
①∠A+∠B=∠C;②
∠A:∠B:∠C=1:2:3;③∠A=90°-∠B;??④∠A=∠B=∠C;
⑥∠A-∠B=∠C;⑦∠A=2∠B=3∠C
;⑧∠A=∠B=∠C
【例2-4】如图,在△ABC中,∠ABC=60?,∠ACB=54?,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,HD是∠BHC的平分线,求∠ABE,∠ACF和∠CHB的度数。
三角形的外角
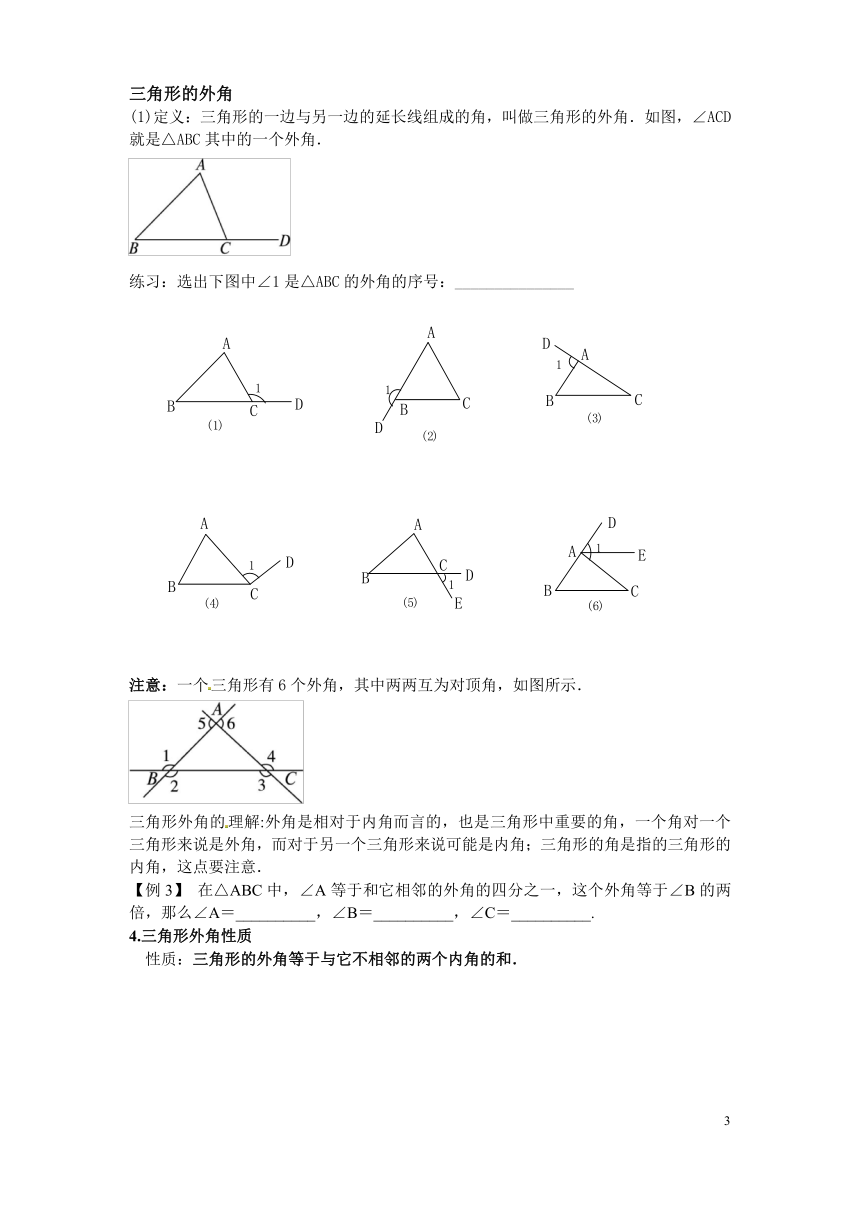
(1)定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.如图,∠ACD就是△ABC其中的一个外角.
练习:选出下图中∠1是△ABC的外角的序号:_______________
注意:一个三角形有6个外角,其中两两互为对顶角,如图所示.
三角形外角的理解:外角是相对于内角而言的,也是三角形中重要的角,一个角对一个三角形来说是外角,而对于另一个三角形来说可能是内角;三角形的角是指的三角形的内角,这点要注意.
【例3】
在△ABC中,∠A等于和它相邻的外角的四分之一,这个外角等于∠B的两倍,那么∠A=__________,∠B=__________,∠C=__________.
4.三角形外角性质
性质:三角形的外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角
如图所示:
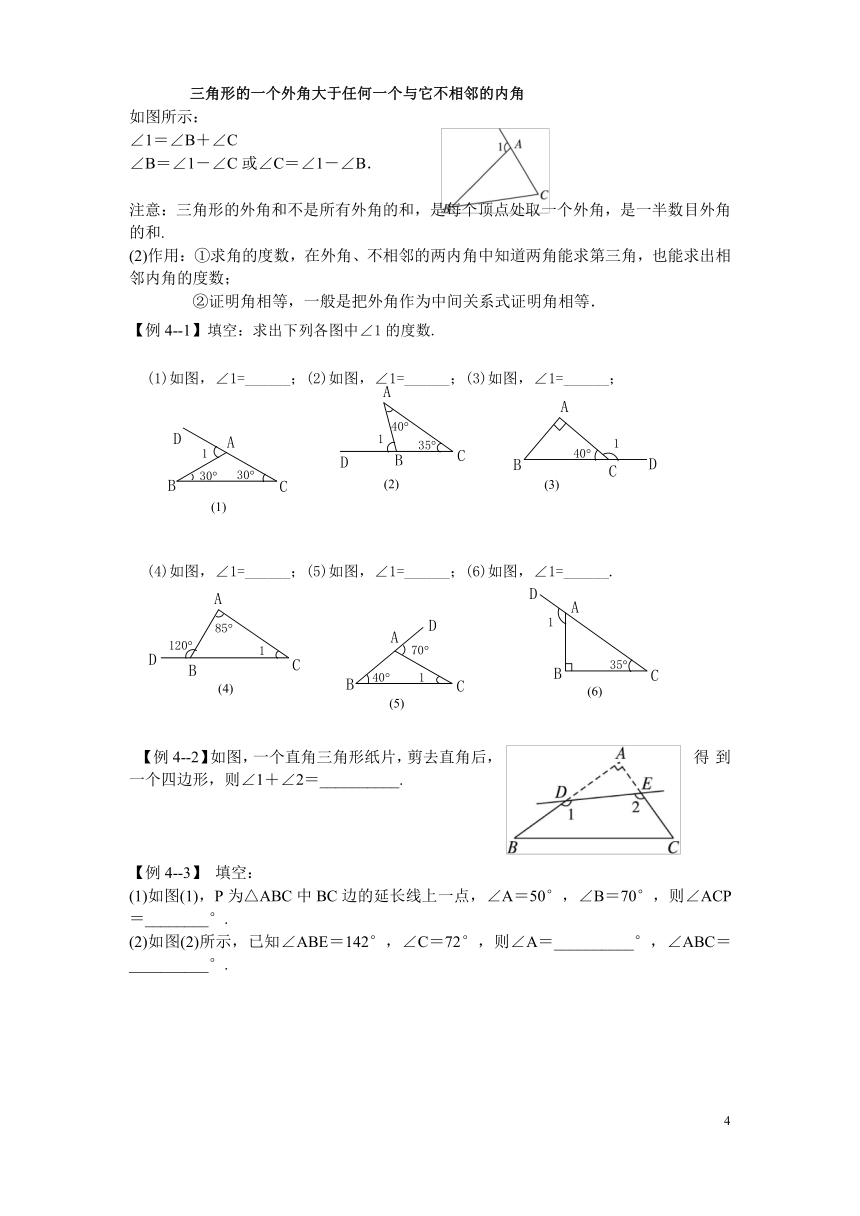
∠1=∠B+∠C
∠B=∠1-∠C或∠C=∠1-∠B.
注意:三角形的外角和不是所有外角的和,是每个顶点处取一个外角,是一半数目外角的和.
(2)作用:①求角的度数,在外角、不相邻的两内角中知道两角能求第三角,也能求出相邻内角的度数;
②证明角相等,一般是把外角作为中间关系式证明角相等.
【例4--1】填空:求出下列各图中∠1的度数.
(1)如图,∠1=______;(2)如图,∠1=______;(3)如图,∠1=______;
(4)如图,∠1=______;(5)如图,∠1=______;(6)如图,∠1=______.
【例4--2】如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=__________.
【例4--3】
填空:
(1)如图(1),P为△ABC中BC边的延长线上一点,∠A=50°,∠B=70°,则∠ACP=________°.
(2)如图(2)所示,已知∠ABE=142°,∠C=72°,则∠A=__________°,∠ABC=__________°.
(3)如图(3),∠3=120°,则∠1-∠2=________°.
图4
【例4--4】如图4,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=________.
三角形外角和
(1)定义:如图所示,在每一个顶点上取一个外角,如∠1,∠2,∠3,它们的和叫做三角形的外角和.
(2)三角形外角和定理:三角形的外角和等于360°.
注意:三角形的外角和不是所有外角的和,是每个顶点处取一个外角,是一半数目外角的和.
【例5】
如图所示.用两种方法说明∠1+∠2+∠3=360°.
多边形内角和
多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
多边形的分类:
多边形可分为凸多边形和凹多边形,画出多边形的任何一条边所在的直线,如果整个多边形都在这条直线的同一侧,则此多边形为凸多边形,反之为凹多边形(见图1).本章所讲的多边形都是指凸多边形.
凸多边形
凹多边形
正多边形
各个角都相等、各个边都相等的多边形叫做正多边形。如正三角形、正方形、正五边形等。
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
思考:五边形共有_______条对角线,n边形共有_______条对角线。
多边形内角和:
…………
从五边形的一个顶点出发,可以作______条对角线,它们将五边形分为______个三角形,五边形的内角和等于180°×_____________;从六边形的一个顶点出发,可以作______条对角线,它们将六边形分为______个三角形,五边形的内角和等于180°×_____________;从n边形的一个顶点出发,可以作______条对角线,它们将n边形分为______个三角形,n
边形的内角和等于180°×_____________。
n边形的内角和等于___________。
【例6--1】在四边形ABCD中,∠A+∠C=180°,∠B∶∠C∶∠D=1∶2∶3,则∠A=________.
【例6--2】如图,DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,则∠B=______
【例6--3】一个多边形内角和是1080°,则这个多边形的边数为(
)
A、
6
B、
7
C、
8
D、
9
【例6--4】一个多边形共有20条对角线,则多边形的边数是(
).
A.6
B.7
C.8
D.9
n边形的外角和等于___________。
【例6--5】一个多边形的内角和是外角和的2倍,则这个多边形(
)
四边形
B.
五边形
C.
六边形
D.
八边形
※.角平分线的夹角与三角形内角关系的探究
(1)三角形的两内角平分线的夹角与内角的关系
如图,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点O,求∠BOC与∠A之间的关系.
(2)三角形两外角的平分线的夹角与内角的关系
如图,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的平分线,试探究∠BPC与∠A的关系.
(3)一个内角平分线与一个外角平分线的夹角与内角的关系
如图,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究
∠BEC与∠A的关系.
【例7-1】
如图,BO,CO分别是∠ABC,∠ACB的两条平分线,∠A=100°,则∠BOC的度数是( ).
A.80°
B.90°
C.120° D.140°
【例7-2】
如图所示,∠ABC的平分线和△ABC的外角∠ACE的平分线交于点D,∠D=30°,∠A的度数是__________;当∠D=__________时,∠A的度数是90°.
作业1:
1.三角形的三个外角之比为,则与之相应的三个内角之比为( )
A.
B.
C.
D.
2.如图,在△ABC中,D是AB上的一点,E是AC上一点,BE.CD相交于F,∠A=70°,∠ACD=20°,∠ABE=28°,则的度数为( )
A.62°
B.68°
C.78°
D.90°
3.若三条线段中,,为奇数,那么由为边组成的三角形共有( )
A.个
B.个
C.无数多个
D.无法确定
4.如果线段能组成三角形,那么它们的长度比可能是( )
A.
B.
C.
D.
5.不一定能构成三角形的一组线段的长度为( )
A.3,7,5
B.3x,4x,5x(x>0)
C.5,5,a(0<a<10)
D.m,m,m2
6.如图1,的平分线交的平分线于,若,则_____.
7.一个三角形中最多有_____个内角是钝角,最多可有_____个角是锐角.
8.三角形两个外角的和等于第三个内角的倍,则第三个内角等于___________.
9.如图2,______;如图3,_____.
10.两根木棒的长分别为和.要选择第三根木棒,将它们钉成一个三角形框架,那么,第三根木棒长()的范围是______.
11.如图,已知∠ACD=120°,∠DFA=122°,∠D=34°,求∠A的度数.
与三角形有关的角
三角形内角和定理
(1)定理:三角形三个内角的和等于180°.
(2)证明方法:证法多样,主要是运用平行线知识把三个角转移成一个平角,从而得到内角和是180°。
①如图所示,过C作CM∥AB,将求∠A+∠B+∠ACB转化为求∠1+∠2+∠ACB,
②过A点作DE∥BC,把求∠BAC+∠B+∠C转化为求∠BAC+∠DAB+∠EAC.
理解与延伸:①一个三角形中最多只有一个钝角或直角;
②一个三角形中最少有一个角不小于60°;
③直角三角形两锐角互余;
④等边三角形每个角都是60°.
(4)作用:求角度,尤其是三角形中的角度计算。
【例1-1】
填空:
(1)在△ABC中,若∠A=80°,∠C=20°,则∠B=__________°;
(2)若∠A=80°,∠B=∠C,则∠C=__________°;
(3)已知△ABC的三个内角的度数之比∠A∶∠B∶∠C=2∶3∶5,则∠B=________°,∠C=_________°.
【例1-2】如图,在△ABC中,∠CAB=∠B=2∠C,AD是∠BAC的平分线,求∠ADC的度数.
【例1-3】如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数。
【例1-4】若等腰三角形的一内角为40°,则顶角为(
)
40°
B.
100°
C.
70°或40°
D.40°或100°
直角三角形的性质与判定
(1)直角三角形的性质:直角三角形的两个锐角互余.
如图所示,在Rt△ABC中,如果∠C=90°,那么∠A+∠B=90°.
【例2-1】
将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是
( ).
A.43°
B.47°
C.30°
D.60°
【例2-2】
如图所示,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P,求证:△EPF是直角三角形.
判定:有两个角互余的三角形是直角三角形。
【例2-3】下列条件能确定△ABC是直角三角形的条件有_____________
①∠A+∠B=∠C;②
∠A:∠B:∠C=1:2:3;③∠A=90°-∠B;??④∠A=∠B=∠C;
⑥∠A-∠B=∠C;⑦∠A=2∠B=3∠C
;⑧∠A=∠B=∠C
【例2-4】如图,在△ABC中,∠ABC=60?,∠ACB=54?,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,HD是∠BHC的平分线,求∠ABE,∠ACF和∠CHB的度数。
三角形的外角
(1)定义:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.如图,∠ACD就是△ABC其中的一个外角.
练习:选出下图中∠1是△ABC的外角的序号:_______________
注意:一个三角形有6个外角,其中两两互为对顶角,如图所示.
三角形外角的理解:外角是相对于内角而言的,也是三角形中重要的角,一个角对一个三角形来说是外角,而对于另一个三角形来说可能是内角;三角形的角是指的三角形的内角,这点要注意.
【例3】
在△ABC中,∠A等于和它相邻的外角的四分之一,这个外角等于∠B的两倍,那么∠A=__________,∠B=__________,∠C=__________.
4.三角形外角性质
性质:三角形的外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角
如图所示:
∠1=∠B+∠C
∠B=∠1-∠C或∠C=∠1-∠B.
注意:三角形的外角和不是所有外角的和,是每个顶点处取一个外角,是一半数目外角的和.
(2)作用:①求角的度数,在外角、不相邻的两内角中知道两角能求第三角,也能求出相邻内角的度数;
②证明角相等,一般是把外角作为中间关系式证明角相等.
【例4--1】填空:求出下列各图中∠1的度数.
(1)如图,∠1=______;(2)如图,∠1=______;(3)如图,∠1=______;
(4)如图,∠1=______;(5)如图,∠1=______;(6)如图,∠1=______.
【例4--2】如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=__________.
【例4--3】
填空:
(1)如图(1),P为△ABC中BC边的延长线上一点,∠A=50°,∠B=70°,则∠ACP=________°.
(2)如图(2)所示,已知∠ABE=142°,∠C=72°,则∠A=__________°,∠ABC=__________°.
(3)如图(3),∠3=120°,则∠1-∠2=________°.
图4
【例4--4】如图4,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=________.
三角形外角和
(1)定义:如图所示,在每一个顶点上取一个外角,如∠1,∠2,∠3,它们的和叫做三角形的外角和.
(2)三角形外角和定理:三角形的外角和等于360°.
注意:三角形的外角和不是所有外角的和,是每个顶点处取一个外角,是一半数目外角的和.
【例5】
如图所示.用两种方法说明∠1+∠2+∠3=360°.
多边形内角和
多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
多边形的分类:
多边形可分为凸多边形和凹多边形,画出多边形的任何一条边所在的直线,如果整个多边形都在这条直线的同一侧,则此多边形为凸多边形,反之为凹多边形(见图1).本章所讲的多边形都是指凸多边形.
凸多边形
凹多边形
正多边形
各个角都相等、各个边都相等的多边形叫做正多边形。如正三角形、正方形、正五边形等。
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
思考:五边形共有_______条对角线,n边形共有_______条对角线。
多边形内角和:
…………
从五边形的一个顶点出发,可以作______条对角线,它们将五边形分为______个三角形,五边形的内角和等于180°×_____________;从六边形的一个顶点出发,可以作______条对角线,它们将六边形分为______个三角形,五边形的内角和等于180°×_____________;从n边形的一个顶点出发,可以作______条对角线,它们将n边形分为______个三角形,n
边形的内角和等于180°×_____________。
n边形的内角和等于___________。
【例6--1】在四边形ABCD中,∠A+∠C=180°,∠B∶∠C∶∠D=1∶2∶3,则∠A=________.
【例6--2】如图,DC∥AB,∠BAE=∠BCD,AE⊥DE,∠D=130°,则∠B=______
【例6--3】一个多边形内角和是1080°,则这个多边形的边数为(
)
A、
6
B、
7
C、
8
D、
9
【例6--4】一个多边形共有20条对角线,则多边形的边数是(
).
A.6
B.7
C.8
D.9
n边形的外角和等于___________。
【例6--5】一个多边形的内角和是外角和的2倍,则这个多边形(
)
四边形
B.
五边形
C.
六边形
D.
八边形
※.角平分线的夹角与三角形内角关系的探究
(1)三角形的两内角平分线的夹角与内角的关系
如图,在△ABC中,∠ABC的平分线与∠ACB的平分线交于点O,求∠BOC与∠A之间的关系.
(2)三角形两外角的平分线的夹角与内角的关系
如图,在△ABC中,BP,CP分别是△ABC的外角∠DBC和∠ECB的平分线,试探究∠BPC与∠A的关系.
(3)一个内角平分线与一个外角平分线的夹角与内角的关系
如图,在△ABC中,CE平分∠ACB,BE是△ABC的外角∠ABD的平分线,试探究
∠BEC与∠A的关系.
【例7-1】
如图,BO,CO分别是∠ABC,∠ACB的两条平分线,∠A=100°,则∠BOC的度数是( ).
A.80°
B.90°
C.120° D.140°
【例7-2】
如图所示,∠ABC的平分线和△ABC的外角∠ACE的平分线交于点D,∠D=30°,∠A的度数是__________;当∠D=__________时,∠A的度数是90°.
作业1:
1.三角形的三个外角之比为,则与之相应的三个内角之比为( )
A.
B.
C.
D.
2.如图,在△ABC中,D是AB上的一点,E是AC上一点,BE.CD相交于F,∠A=70°,∠ACD=20°,∠ABE=28°,则的度数为( )
A.62°
B.68°
C.78°
D.90°
3.若三条线段中,,为奇数,那么由为边组成的三角形共有( )
A.个
B.个
C.无数多个
D.无法确定
4.如果线段能组成三角形,那么它们的长度比可能是( )
A.
B.
C.
D.
5.不一定能构成三角形的一组线段的长度为( )
A.3,7,5
B.3x,4x,5x(x>0)
C.5,5,a(0<a<10)
D.m,m,m2
6.如图1,的平分线交的平分线于,若,则_____.
7.一个三角形中最多有_____个内角是钝角,最多可有_____个角是锐角.
8.三角形两个外角的和等于第三个内角的倍,则第三个内角等于___________.
9.如图2,______;如图3,_____.
10.两根木棒的长分别为和.要选择第三根木棒,将它们钉成一个三角形框架,那么,第三根木棒长()的范围是______.
11.如图,已知∠ACD=120°,∠DFA=122°,∠D=34°,求∠A的度数.
