人教版八年级上册:12.1 全等三角形 讲义(知识点+练习)(无答案)
文档属性
| 名称 | 人教版八年级上册:12.1 全等三角形 讲义(知识点+练习)(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 165.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
图片预览


文档简介
全等形和全等三角形
全等三角形:能够完全重合的两个图形叫做全等形,能够完全重合的两个三角形叫做全等三角形。
一个图形经过平移、翻折、旋转后位置变化了,但是形状、大小都没有改变,即平移、翻折、旋转后的图形全等。
重合的顶点叫做对应点:A→D,B→E,C→F;
重合的边叫做对应边:AB→DE,AC→DF,BC→EF;
重合的角叫做对应角:∠A→∠D,∠B→∠E,∠C→∠F
;
记作△ABC≌DEF
全等三角形的性质:
全等三角形对应边相等,全等三角形对应角相等。
即AB=DE,AC=DF,BC=EF;∠A=∠D,∠B=∠E,∠C=∠F
【例1--1】:△ABC≌△DEF,∠A的对应角是∠D,∠B的对应角∠E,则∠C与
______
是对应角;AB与
____
是对应边,BC与
_______
是对应边,AC与
_______
是对应边.
【例1--2】如图的两个三角形全等.∠B和∠D,∠BAC与∠DCA是对应角。
(1)若按对应顶点写在对应位置上,则应写为△ABC≌__________????.
(2)找出对应边和对应角.
【例1--3】如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,
∠D=35°,∠C=60°(1)求线段AE的长。
(2)求∠DFA的度数。
【例1--4】如图,A、D.?E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
全等三角形的判定
Ⅰ。边边边(SSS)
三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”)。
书写格式:
在△ABC和△A’B’C’中,
∵
∴△ABC≌△A’B’C’(SSS)
【例2--1】:如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形有(
)
A.?4对
B.?3对
C.?2对
D.?1对
练习:如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.
若AC=BD,AB=ED,BC=BE,则
∠ACB等于(
)
A.?∠EDB
B.?∠BED
C.?∠AFB
D.?2∠ABF
【例2--2】如图,点B,E,C,F在同一条直线上,AB=DF,AC=DE,BE=FC.
(1)证明:△ABC≌△DEF.
(2)若∠A=65°,求∠D的度数.
【例2--3】如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架。
求证:△ABD≌△ACD.
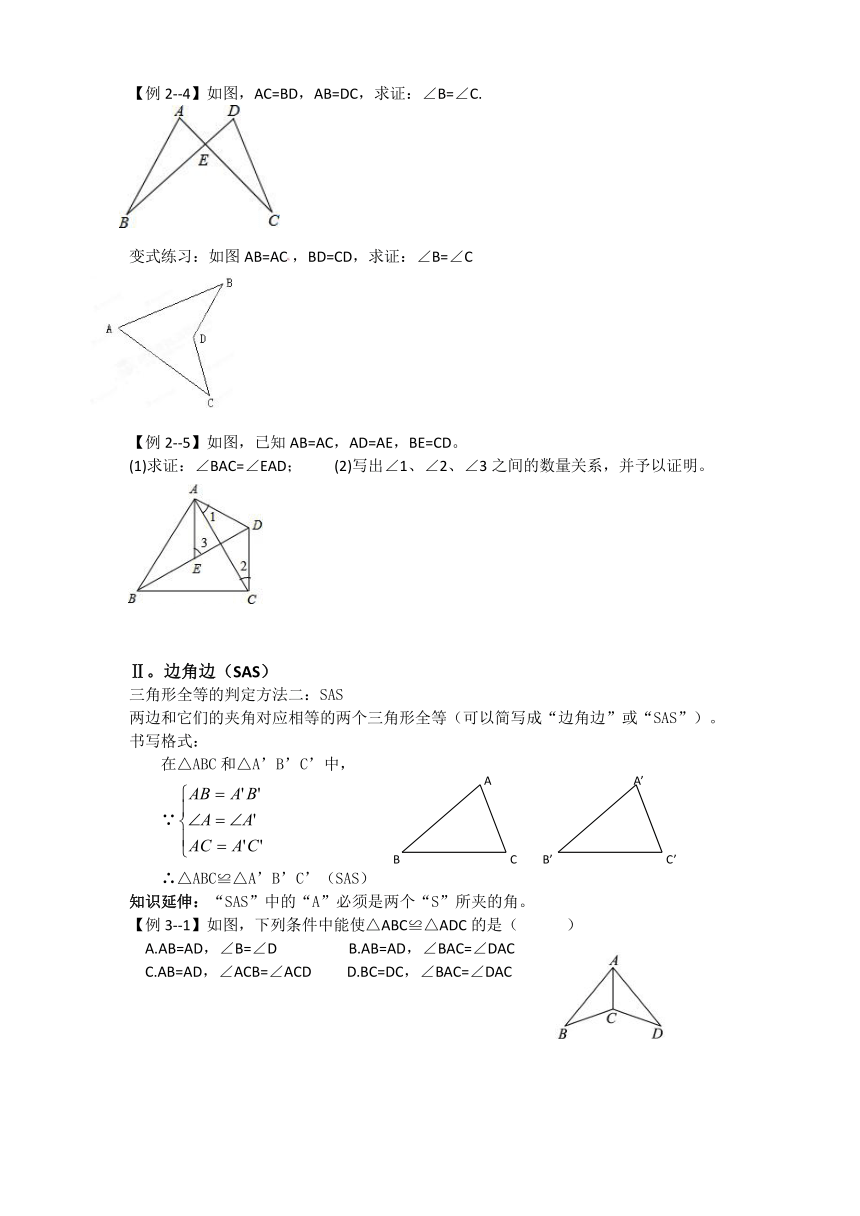
【例2--4】如图,AC=BD,AB=DC,求证:∠B=∠C.
变式练习:如图AB=AC,BD=CD,求证:∠B=∠C
【例2--5】如图,已知AB=AC,AD=AE,BE=CD。
(1)求证:∠BAC=∠EAD;
(2)写出∠1、∠2、∠3之间的数量关系,并予以证明。
Ⅱ。边角边(SAS)
三角形全等的判定方法二:SAS
两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”)。
书写格式:
在△ABC和△A’B’C’中,
∵
∴△ABC≌△A’B’C’(SAS)
知识延伸:“SAS”中的“A”必须是两个“S”所夹的角。
【例3--1】如图,下列条件中能使△ABC≌△ADC的是(
)
A.AB=AD,∠B=∠D
B.AB=AD,∠BAC=∠DAC
C.AB=AD,∠ACB=∠ACD
?D.BC=DC,∠BAC=∠DAC
练习:如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则可增加的条件是(
)
A.?∠ABE=∠DBE
B.?∠A=∠D
C.?∠E=∠C
D.?∠1=∠2
【例3--2】
如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
【例3--3】如图,已知AB=AD,BC=DC.求证:OB=OD.
【例3--4】如图,点D.?E分别是AB、AC上的点,AD=AE,BD=CE.
求证:∠B=∠C.
练习:1.如图,AB,CD交于O点,且互相平分,则图中的全等三角形有(
)
A.2对
B.3对
C.4对
D.5对
2.如图,已知AB∥CD,AB=CD,AF=CE,判断DF与BE是否平行,并说明理由。
3.如图,OA=OB,OC=OD,∠O=60?,∠C=25?,则∠BED=______度。
【例3--5】
如图,点E,
F在BC上,BE=CF,
AB=DC,
∠B=∠C.
求证:
∠A=∠D
作业3:
1.如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定(
?)
A.?△ABD≌△ACD
B.?△ABE≌△ACE
C.?△BED≌△CED
D.?△ABE≌△EDC
2.如图2,△ABC≌△DEC,∠A=70?,∠ACB=60?,则∠E的度数为(
)
A.?70?
B.?50?
C.?60?
D.?30?
3.如图3所示,AC=DF,BD=EC,AC∥DF,∠ACB=80?,∠B=30?,则∠F=___.
图2
图3
图4
4.如图3,已知∠l=∠2,AD
=AC,则△______≌△_______
,其依据是_____________。
5.如图4,∠l=∠2,AB
=AC,AE=AD,则△ABD≌△______,依据是_____________,由此还可得BD=______。
6.如图,已知△ACE≌△DBF,点A.
B.
C.?D在同一条直线上,AE=DF,CE=BF,AD=8,BC=2.
(1)求AC的长;(2)求证:CE∥BF.
7.如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4.
?(1)直接写出梯形BDEC的面积为___________.
?(2)求证:AB=AC.
?(3)求AB长的范围。
8.如图所示,AC=DF,BD=EC,AC∥DF,∠ACB=80?,∠B=30?,求∠F.
全等三角形:能够完全重合的两个图形叫做全等形,能够完全重合的两个三角形叫做全等三角形。
一个图形经过平移、翻折、旋转后位置变化了,但是形状、大小都没有改变,即平移、翻折、旋转后的图形全等。
重合的顶点叫做对应点:A→D,B→E,C→F;
重合的边叫做对应边:AB→DE,AC→DF,BC→EF;
重合的角叫做对应角:∠A→∠D,∠B→∠E,∠C→∠F
;
记作△ABC≌DEF
全等三角形的性质:
全等三角形对应边相等,全等三角形对应角相等。
即AB=DE,AC=DF,BC=EF;∠A=∠D,∠B=∠E,∠C=∠F
【例1--1】:△ABC≌△DEF,∠A的对应角是∠D,∠B的对应角∠E,则∠C与
______
是对应角;AB与
____
是对应边,BC与
_______
是对应边,AC与
_______
是对应边.
【例1--2】如图的两个三角形全等.∠B和∠D,∠BAC与∠DCA是对应角。
(1)若按对应顶点写在对应位置上,则应写为△ABC≌__________????.
(2)找出对应边和对应角.
【例1--3】如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,
∠D=35°,∠C=60°(1)求线段AE的长。
(2)求∠DFA的度数。
【例1--4】如图,A、D.?E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
全等三角形的判定
Ⅰ。边边边(SSS)
三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”)。
书写格式:
在△ABC和△A’B’C’中,
∵
∴△ABC≌△A’B’C’(SSS)
【例2--1】:如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形有(
)
A.?4对
B.?3对
C.?2对
D.?1对
练习:如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.
若AC=BD,AB=ED,BC=BE,则
∠ACB等于(
)
A.?∠EDB
B.?∠BED
C.?∠AFB
D.?2∠ABF
【例2--2】如图,点B,E,C,F在同一条直线上,AB=DF,AC=DE,BE=FC.
(1)证明:△ABC≌△DEF.
(2)若∠A=65°,求∠D的度数.
【例2--3】如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架。
求证:△ABD≌△ACD.
【例2--4】如图,AC=BD,AB=DC,求证:∠B=∠C.
变式练习:如图AB=AC,BD=CD,求证:∠B=∠C
【例2--5】如图,已知AB=AC,AD=AE,BE=CD。
(1)求证:∠BAC=∠EAD;
(2)写出∠1、∠2、∠3之间的数量关系,并予以证明。
Ⅱ。边角边(SAS)
三角形全等的判定方法二:SAS
两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”)。
书写格式:
在△ABC和△A’B’C’中,
∵
∴△ABC≌△A’B’C’(SAS)
知识延伸:“SAS”中的“A”必须是两个“S”所夹的角。
【例3--1】如图,下列条件中能使△ABC≌△ADC的是(
)
A.AB=AD,∠B=∠D
B.AB=AD,∠BAC=∠DAC
C.AB=AD,∠ACB=∠ACD
?D.BC=DC,∠BAC=∠DAC
练习:如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则可增加的条件是(
)
A.?∠ABE=∠DBE
B.?∠A=∠D
C.?∠E=∠C
D.?∠1=∠2
【例3--2】
如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
【例3--3】如图,已知AB=AD,BC=DC.求证:OB=OD.
【例3--4】如图,点D.?E分别是AB、AC上的点,AD=AE,BD=CE.
求证:∠B=∠C.
练习:1.如图,AB,CD交于O点,且互相平分,则图中的全等三角形有(
)
A.2对
B.3对
C.4对
D.5对
2.如图,已知AB∥CD,AB=CD,AF=CE,判断DF与BE是否平行,并说明理由。
3.如图,OA=OB,OC=OD,∠O=60?,∠C=25?,则∠BED=______度。
【例3--5】
如图,点E,
F在BC上,BE=CF,
AB=DC,
∠B=∠C.
求证:
∠A=∠D
作业3:
1.如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定(
?)
A.?△ABD≌△ACD
B.?△ABE≌△ACE
C.?△BED≌△CED
D.?△ABE≌△EDC
2.如图2,△ABC≌△DEC,∠A=70?,∠ACB=60?,则∠E的度数为(
)
A.?70?
B.?50?
C.?60?
D.?30?
3.如图3所示,AC=DF,BD=EC,AC∥DF,∠ACB=80?,∠B=30?,则∠F=___.
图2
图3
图4
4.如图3,已知∠l=∠2,AD
=AC,则△______≌△_______
,其依据是_____________。
5.如图4,∠l=∠2,AB
=AC,AE=AD,则△ABD≌△______,依据是_____________,由此还可得BD=______。
6.如图,已知△ACE≌△DBF,点A.
B.
C.?D在同一条直线上,AE=DF,CE=BF,AD=8,BC=2.
(1)求AC的长;(2)求证:CE∥BF.
7.如图,BD⊥DE于D,CE⊥DE于E,AD=CE=2,BD=AE=4.
?(1)直接写出梯形BDEC的面积为___________.
?(2)求证:AB=AC.
?(3)求AB长的范围。
8.如图所示,AC=DF,BD=EC,AC∥DF,∠ACB=80?,∠B=30?,求∠F.
