人教版八年级上册:12.2 三角形全等的判定(ASA、AAS、HL)讲义(知识点+练习)(无答案)
文档属性
| 名称 | 人教版八年级上册:12.2 三角形全等的判定(ASA、AAS、HL)讲义(知识点+练习)(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
图片预览


文档简介
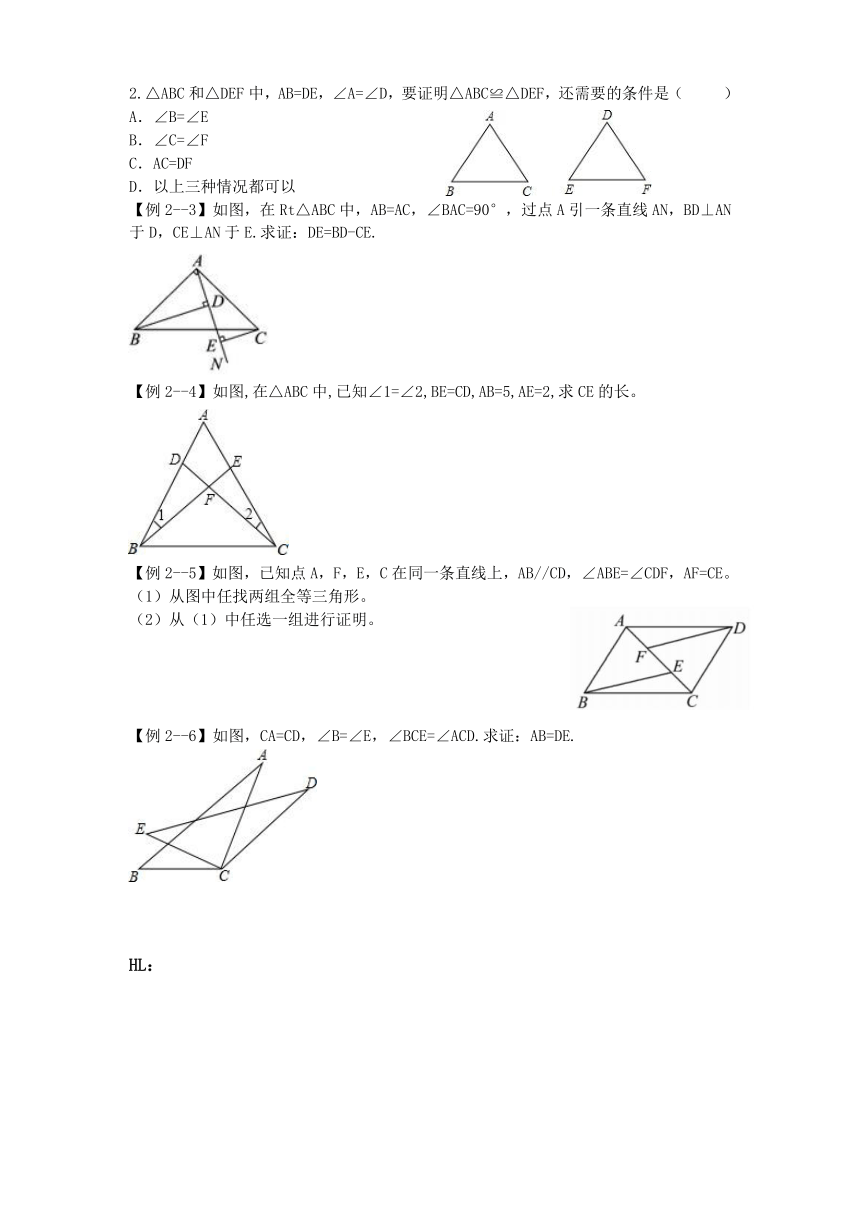
全等三角形的判定2(ASA、AAS、HL)
ASA
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
书写格式:
在△ABC和△A’B’C’中,
∵
∴△ABC≌△A’B’C’(ASA)
知识延伸:“ASA”中的“S”必须是两个“A”所夹的边。
【例1--1】如图,下列条件不能证明△ABC≌△DCB的是(
)
A.?AB=DC,AC=DB
B.?AB=DC,∠ABC=∠DCB
C.?BO=CO,∠A=∠D
D.?AB=DC,∠A=∠D
练习:如图,AB=AC,若利用“ASA”来证明△ABE≌△ACD,需补充的一个条件是____________.
【例1--2】如图,AB∥CD,AF∥DE,BE=CF,求证:AB=CD.
【例1--3】如图,点B在射线AE上,∠1=∠2,∠3=∠4.求证:AC=AD.
【例1--4】如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.
AAS
判定方法:
两个角和其中一个角的对边对应相等的两个三角形全等.
(可以简写成“角角边”或“AAS”)。
书写格式:在△ABC和△A’B’C’中,
∵
∴△ABC≌△A’B’C’(AAS)
知识延伸:“AAS”可以看成是“ASA”的推论。
规律方法小结:由“角边角”及“角角边”可知两角及一边对应相等的两个三角形全等。无论这个一边是“对边”还是“夹边”,只要对应相等即可。
【例2--1】如图1,已知△ABC的六个元素,则图2甲、乙、丙三个三角形中和图1△ABC全等的图形是(?)
A.
甲乙
B.
丙
C.
乙丙
D.
乙
【例2--2】在△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列条件中错误的是(?
)
A.?AC=DF
B.?BC=EF
C.?∠A=∠D
D.?∠C=∠F
练习:1.两个等腰三角形,若顶角和底边对应相等,则两个等腰三角形全等,其理由是(
)
A.SAS
B.SSS
C.ASA
D.ASA或AAS
2.△ABC和△DEF中,AB=DE,∠A=∠D,要证明△ABC≌△DEF,还需要的条件是(
)
A.∠B=∠E
B.∠C=∠F
C.AC=DF
D.以上三种情况都可以
【例2--3】如图,在Rt△ABC中,AB=AC,∠BAC=90°,过点A引一条直线AN,BD⊥AN于D,CE⊥AN于E.求证:DE=BD-CE.
【例2--4】如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,求CE的长。
【例2--5】如图,已知点A,F,E,C在同一条直线上,AB//CD,∠ABE=∠CDF,AF=CE。
(1)从图中任找两组全等三角形。
(2)从(1)中任选一组进行证明。
【例2--6】如图,CA=CD,∠B=∠E,∠BCE=∠ACD.求证:AB=DE.
HL:
斜边和一条直角边分别相等的两个直角三角形全等。(简写成“斜边、直角边”或者HL)
应用格式:如图在三角形Rt△ABC≌Rt△DEF中
∴Rt△ABC≌Rt△DEF(_________)
【例3--1】如图所示,∠C=∠D=90?添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等。以下给出的条件适合的是(
)
?AC=AD
B.?AB=AB
C.?∠ABC=∠ABD
D.?∠BAC=∠BAD
练习:下列条件不能判断两个直角三角形全等的是(
?)
A.
两条直角边分别对应相等
斜边和一个锐角分别对应相等
C.
两个锐角对应相等
D.
斜边和一直角边分别对应相等
【例3--2】如图,MN∥PQ,AB⊥PQ,点A.
D.
B.?C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=___.
练习:如图,∠C=90?,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=___,△ABC与△APQ全等。
【例3--3】如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证:
(1)△ABC≌△EFD;??
(2)AB∥EF.
【例3--4】如图,OA=0B,AC=BD,0A⊥AC,0B⊥BD,OM⊥CD于M,求证:OM平分∠A0B.
【例3--5】如图所示,太阳光线AC和A`C`是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?说明理由。
【例3--6】在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图1所示)且AD=CE.求证:AB⊥AC.
(2)若B、C在DE的两侧(如图2所示),其他条件不变,AB与AC仍垂直吗?若是,请给出证明;若不是,请说明理由.
作业4:
1.如图,已知EC=BF,∠A=∠D,现从下列6个条件:①AC=DF;②∠B=∠E;③∠ACB=∠DFE;④AB∥ED;⑤AB=ED;⑥DF∥AC;从中选取一个条件,以保证△ABC≌△DEF,则可选择的是(
)
A.
②③④⑥
B.
③④⑤⑥
C.
①③④⑥
D.
①②③④
2.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是(
)
A.AE=DF
B.∠A=∠D
C.∠B=∠C
D.AB=DC
3.如图:∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为
。
4.如图,在△ABC中,AD⊥BC于D,再添加一个条件
(只需填一个),就可以判定△ABD≌△ACD.
5.在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AB=AC.
6.如图,E、A、C三点共线,AB∥CD,∠B=∠E,AC=CD。求证:BC=ED。
7.已知:BE⊥CD,BE=DE,BC=DA,
求证:①
△BEC≌△DAE;
②DF⊥BC.
ASA
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
书写格式:
在△ABC和△A’B’C’中,
∵
∴△ABC≌△A’B’C’(ASA)
知识延伸:“ASA”中的“S”必须是两个“A”所夹的边。
【例1--1】如图,下列条件不能证明△ABC≌△DCB的是(
)
A.?AB=DC,AC=DB
B.?AB=DC,∠ABC=∠DCB
C.?BO=CO,∠A=∠D
D.?AB=DC,∠A=∠D
练习:如图,AB=AC,若利用“ASA”来证明△ABE≌△ACD,需补充的一个条件是____________.
【例1--2】如图,AB∥CD,AF∥DE,BE=CF,求证:AB=CD.
【例1--3】如图,点B在射线AE上,∠1=∠2,∠3=∠4.求证:AC=AD.
【例1--4】如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.
AAS
判定方法:
两个角和其中一个角的对边对应相等的两个三角形全等.
(可以简写成“角角边”或“AAS”)。
书写格式:在△ABC和△A’B’C’中,
∵
∴△ABC≌△A’B’C’(AAS)
知识延伸:“AAS”可以看成是“ASA”的推论。
规律方法小结:由“角边角”及“角角边”可知两角及一边对应相等的两个三角形全等。无论这个一边是“对边”还是“夹边”,只要对应相等即可。
【例2--1】如图1,已知△ABC的六个元素,则图2甲、乙、丙三个三角形中和图1△ABC全等的图形是(?)
A.
甲乙
B.
丙
C.
乙丙
D.
乙
【例2--2】在△ABC和△DEF中,AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列条件中错误的是(?
)
A.?AC=DF
B.?BC=EF
C.?∠A=∠D
D.?∠C=∠F
练习:1.两个等腰三角形,若顶角和底边对应相等,则两个等腰三角形全等,其理由是(
)
A.SAS
B.SSS
C.ASA
D.ASA或AAS
2.△ABC和△DEF中,AB=DE,∠A=∠D,要证明△ABC≌△DEF,还需要的条件是(
)
A.∠B=∠E
B.∠C=∠F
C.AC=DF
D.以上三种情况都可以
【例2--3】如图,在Rt△ABC中,AB=AC,∠BAC=90°,过点A引一条直线AN,BD⊥AN于D,CE⊥AN于E.求证:DE=BD-CE.
【例2--4】如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,求CE的长。
【例2--5】如图,已知点A,F,E,C在同一条直线上,AB//CD,∠ABE=∠CDF,AF=CE。
(1)从图中任找两组全等三角形。
(2)从(1)中任选一组进行证明。
【例2--6】如图,CA=CD,∠B=∠E,∠BCE=∠ACD.求证:AB=DE.
HL:
斜边和一条直角边分别相等的两个直角三角形全等。(简写成“斜边、直角边”或者HL)
应用格式:如图在三角形Rt△ABC≌Rt△DEF中
∴Rt△ABC≌Rt△DEF(_________)
【例3--1】如图所示,∠C=∠D=90?添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等。以下给出的条件适合的是(
)
?AC=AD
B.?AB=AB
C.?∠ABC=∠ABD
D.?∠BAC=∠BAD
练习:下列条件不能判断两个直角三角形全等的是(
?)
A.
两条直角边分别对应相等
斜边和一个锐角分别对应相等
C.
两个锐角对应相等
D.
斜边和一直角边分别对应相等
【例3--2】如图,MN∥PQ,AB⊥PQ,点A.
D.
B.?C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=___.
练习:如图,∠C=90?,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=___,△ABC与△APQ全等。
【例3--3】如图,AB=EF,BC⊥AE于C,FD⊥AE于D,CE=DA.求证:
(1)△ABC≌△EFD;??
(2)AB∥EF.
【例3--4】如图,OA=0B,AC=BD,0A⊥AC,0B⊥BD,OM⊥CD于M,求证:OM平分∠A0B.
【例3--5】如图所示,太阳光线AC和A`C`是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?说明理由。
【例3--6】在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图1所示)且AD=CE.求证:AB⊥AC.
(2)若B、C在DE的两侧(如图2所示),其他条件不变,AB与AC仍垂直吗?若是,请给出证明;若不是,请说明理由.
作业4:
1.如图,已知EC=BF,∠A=∠D,现从下列6个条件:①AC=DF;②∠B=∠E;③∠ACB=∠DFE;④AB∥ED;⑤AB=ED;⑥DF∥AC;从中选取一个条件,以保证△ABC≌△DEF,则可选择的是(
)
A.
②③④⑥
B.
③④⑤⑥
C.
①③④⑥
D.
①②③④
2.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是(
)
A.AE=DF
B.∠A=∠D
C.∠B=∠C
D.AB=DC
3.如图:∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为
。
4.如图,在△ABC中,AD⊥BC于D,再添加一个条件
(只需填一个),就可以判定△ABD≌△ACD.
5.在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AB=AC.
6.如图,E、A、C三点共线,AB∥CD,∠B=∠E,AC=CD。求证:BC=ED。
7.已知:BE⊥CD,BE=DE,BC=DA,
求证:①
△BEC≌△DAE;
②DF⊥BC.
