人教版八年级数学上册 11.1.2三角形的高、中线与角平分线 能力提升卷(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 11.1.2三角形的高、中线与角平分线 能力提升卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 428.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-09 23:56:28 | ||
图片预览


文档简介
人教版八年级数学上册
11.1.2三角形的高、中线与角平分线
能力提升卷
一、选择题(共10小题,3
10=30)
1.如图,以CE为高的三角形有( )
A.9个
B.10个
C.11个
D.12个
2.如图,在△ABC中,D,E两点分别在AB,BC上,若AD∶DB=CE∶EB=2∶3,则△DBE与△ADC的面积比为( )
A.3∶5
B.4∶5
C.9∶10
D.15∶16
3.若线段AM,AN分别是△ABC的BC边上的高线和中线,则( )
A.AM>AN
B.AM≥AN
C.AM<AN
D.AM≤AN
4.如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,S△ABC=4
cm2,则S△BEF等于( )
A.2
cm2
B.1
cm2
C.
cm2
D.
cm2
5.如图,AD是△ABC的中线,DE是△ADC的高线,AB=16,AC=22,DE=8,则点D到AB的距离是( )
A.11
B.
C.
D.8
6.
如图,AD是△ABC的中线,若△ABD的周长为25
cm,AB比AC长6
cm,则△ACD的周长为(
)
A.19
cm
B.22
cm
C.25
cm
D.31
cm
7.如图,在△ABC中,AD平分∠BAC交BC于点D,∠B=30°,∠ADC=70°,则∠C的度数是( )
A.50°
B.60°
C.70°
D.80°
8.如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
9.下列说法:①三角形的高、中线、角平分线都是线段;②三角形的三条中线都在三角形的内部;③三角形的高有两条在三角形的外部,还有一条在三角形的内部;④在△ABC中,如果点P是AC边的中点,则PB是△ABC的中线.其中正确的是(
)
A.①②④
B.①②③④
C.①④
D.①②
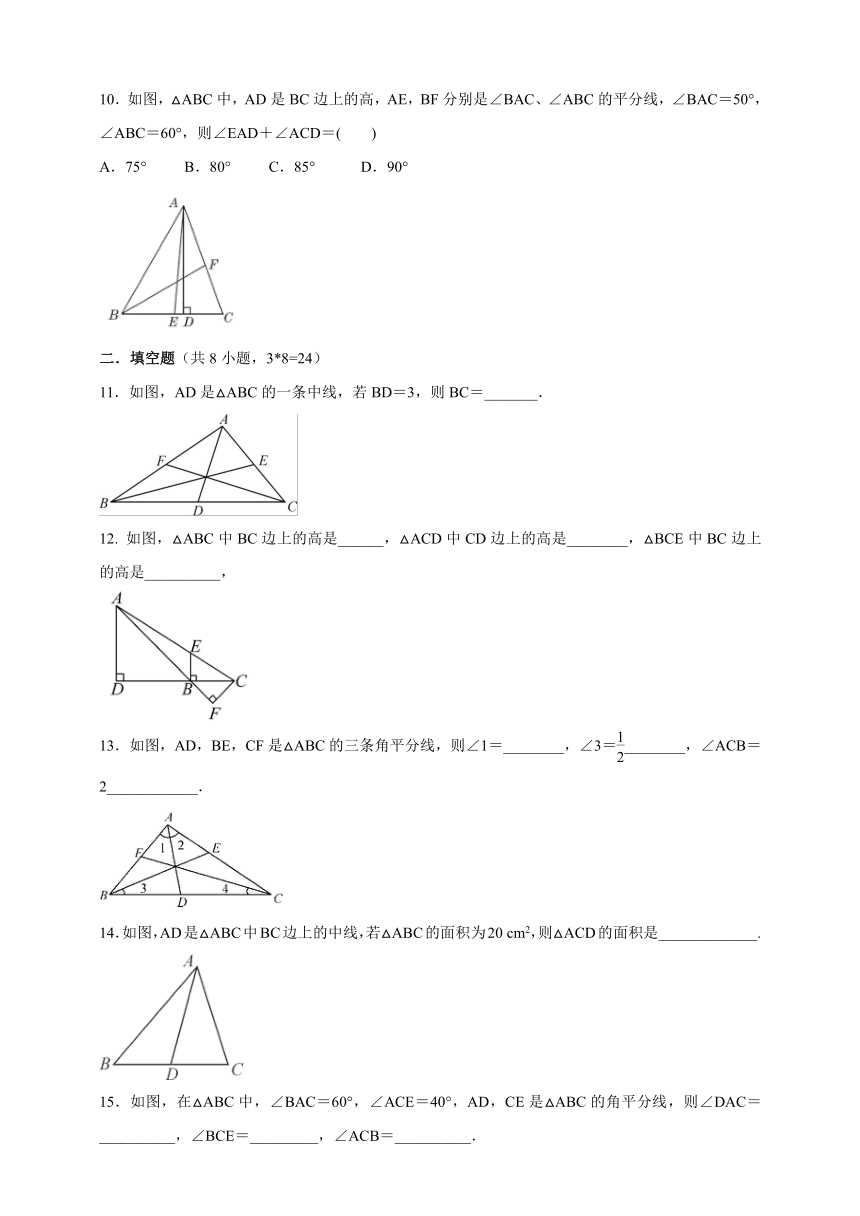
10.如图,△ABC中,AD是BC边上的高,AE,BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75°
B.80°
C.85°
D.90°
二.填空题(共8小题,3
8=24)
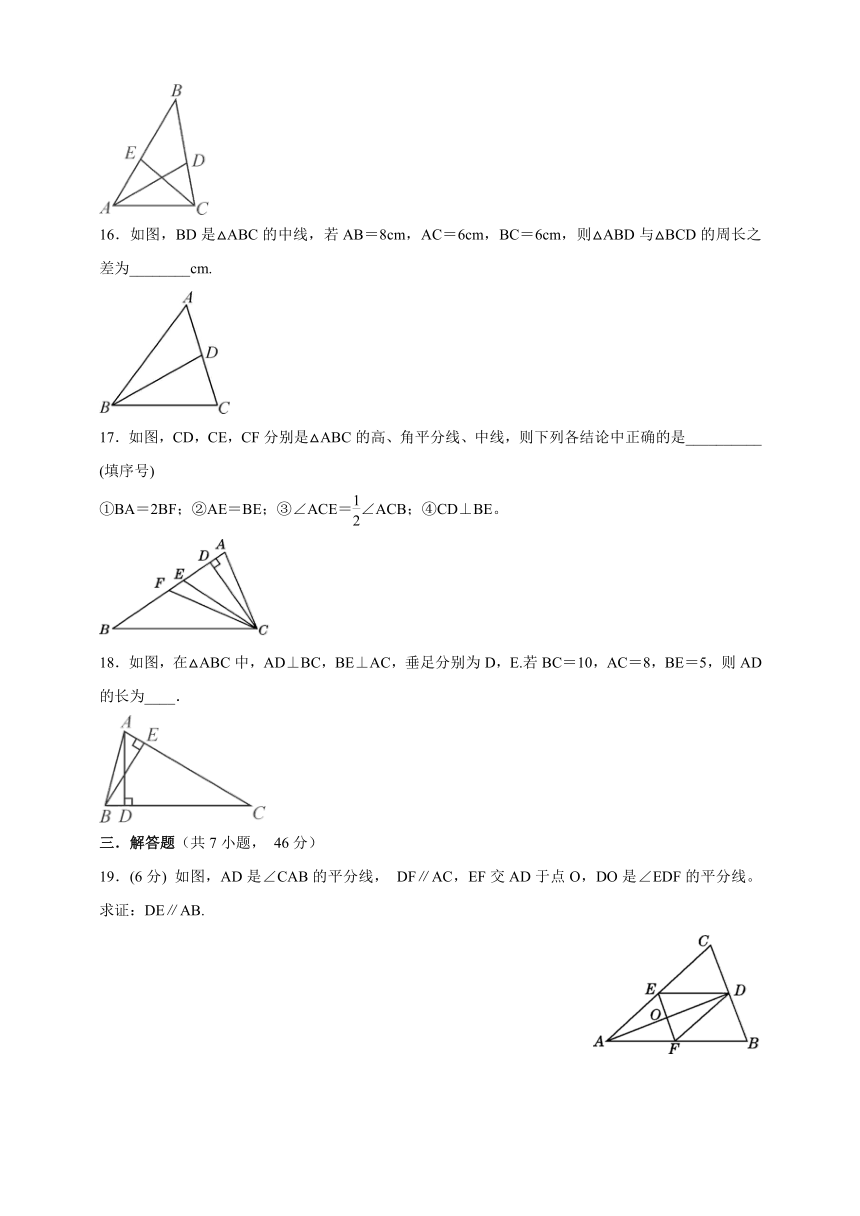
11.如图,AD是△ABC的一条中线,若BD=3,则BC=_______.
12.
如图,△ABC中BC边上的高是______,△ACD中CD边上的高是________,△BCE中BC边上的高是__________,
13.如图,AD,BE,CF是△ABC的三条角平分线,则∠1=________,∠3=________,∠ACB=2____________.
14.如图,AD是△ABC中BC边上的中线,若△ABC的面积为20
cm2,则△ACD的面积是_____________.
15.如图,在△ABC中,∠BAC=60°,∠ACE=40°,AD,CE是△ABC的角平分线,则∠DAC=__________,∠BCE=_________,∠ACB=__________.
16.如图,BD是△ABC的中线,若AB=8cm,AC=6cm,BC=6cm,则△ABD与△BCD的周长之差为________cm.
17.如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各结论中正确的是__________
(填序号)
①BA=2BF;②AE=BE;③∠ACE=∠ACB;④CD⊥BE。
18.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E.若BC=10,AC=8,BE=5,则AD的长为____.
三.解答题(共7小题,
46分)
19.(6分)
如图,AD是∠CAB的平分线,
DF∥AC,EF交AD于点O,DO是∠EDF的平分线。求证:DE∥AB.
20.(6分)
如图,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高;
(2)若△ABD的面积为6,且BD边上的高为3,求BC的长.
21.(6分)
如图,AD是△ABC的角平分线,DE∥AC交AB于E,∠1=∠2,则DF与AB有什么关系?并说明理由.
22.(6分)
如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,且S△ABC
=4cm2,求则S阴影.
23.(6分)
等腰三角形一腰上的中线把该三角形的周长分为13.5和11.5两部分,求这个等腰三角形各边的长.
24.(8分)
如图,在△ABC中,AB>BC,AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
25.(8分)
如图所示,已知AD,AE分别是△ABC的高和中线,AB=6
cm,AC=8
cm,BC=10
cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
参考答案
1-5BCDBA
6-10ACDAA
11.
6
12.
AD,AD,BE
13.
∠2,∠ABC
,∠4(∠ACF)
14.
10
cm2
15.
30°,40°,80°
16.
2
17.
①③④
18.
4
19.
证明:∵DF∥AC,∴∠FDA=∠EAD.
∵AD是∠CAB的平分线,∴∠EAD=∠FAD.
∴∠FAD=∠FDA.
∵DO是∠EDF的平分线,∴∠EDA=∠FDA.
∴∠EDA=∠FAD.
∴DE∥AB.
20.
解:(1)如图所示.
(2)∵AD是△ABC的边BC上的中线,△ABD的面积为6,
∴△ABC的面积为12.
∵BD边上的高为3,
∴BC=12×2÷3=8.
21.
解:DF∥AB.理由:
∵DE∥AC,∴∠1=∠4,
∵AD是△ABC角平分线,∴∠3=∠4,∴∠1=∠3,
又∵∠1=∠2,∴∠2=∠3,
∴DF∥AB
22.
解:∵点D是BC的中点,∴BD=CD.∴S△ABD=S△ACD=S△ABC.
同理,S△BDE
=S△ABE=S△ABD,
S△CDE=S△ACE=S△ACD.
∴S△BCE=S△BDE+
S△CDE=(S△ABD+
S△ACD)=S△ABC=×4=2(cm2).
∵点F是CE的中点,∴S阴影=S△BEF=S△BCE=1(cm2).
23.
解:设在△ABC中,AB=AC,BD是AC边上的中线.
依题意,当AB>BC时,AB-BC=13.5-11.5=2,则AB=BC+2.
所以2(BC+2)+BC=13.5+11.5,
解得BC=7,则AB=AC=BC+2=9.
当AB则BC=AB+2.
所以2AB+AB+2=13.5+11.5,
解得AB=,则AC=,BC=AB+2=.
综上,这个等腰三角形三边的长分别为9,9,7或,,.
24.
解:∵AD是BC边上的中线,∴BD=CD.设BD=CD=x,AB=y.
∵AC=2BC,∴AC=4x.分为两种情况:
①AC+CD=60,AB+BD=40,
则4x+x=60,x+y=40,
解得x=12,y=28,
即AC=4x=48,AB=28;
②AC+CD=40,AB+BD=60,
则4x+x=40,x+y=60,
解得x=8,y=52,
即AC=4x=32,AB=52,BC=2x=16,
此时不符合三角形三边关系.
综上所述,AC=48,AB=28
25.
解:(1)∵∠BAC=90°,AD
是边BC上的高,∴AB·AC=BC·AD,
∴AD===4.8(cm),即AD的长为4.8
cm.
(2)∵△ABC是直角三角形,∠BAC=90°,AB=6
cm,AC=8
cm,
∴S△ABC=AB·AC=×6×8=24(cm2).
又∵AE是△ABC的中线,∴BE=EC,
∴BE·AD=EC·AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12
cm2.∴△ABE的面积是12
cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是2
cm.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
11.1.2三角形的高、中线与角平分线
能力提升卷
一、选择题(共10小题,3
10=30)
1.如图,以CE为高的三角形有( )
A.9个
B.10个
C.11个
D.12个
2.如图,在△ABC中,D,E两点分别在AB,BC上,若AD∶DB=CE∶EB=2∶3,则△DBE与△ADC的面积比为( )
A.3∶5
B.4∶5
C.9∶10
D.15∶16
3.若线段AM,AN分别是△ABC的BC边上的高线和中线,则( )
A.AM>AN
B.AM≥AN
C.AM<AN
D.AM≤AN
4.如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,S△ABC=4
cm2,则S△BEF等于( )
A.2
cm2
B.1
cm2
C.
cm2
D.
cm2
5.如图,AD是△ABC的中线,DE是△ADC的高线,AB=16,AC=22,DE=8,则点D到AB的距离是( )
A.11
B.
C.
D.8
6.
如图,AD是△ABC的中线,若△ABD的周长为25
cm,AB比AC长6
cm,则△ACD的周长为(
)
A.19
cm
B.22
cm
C.25
cm
D.31
cm
7.如图,在△ABC中,AD平分∠BAC交BC于点D,∠B=30°,∠ADC=70°,则∠C的度数是( )
A.50°
B.60°
C.70°
D.80°
8.如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
9.下列说法:①三角形的高、中线、角平分线都是线段;②三角形的三条中线都在三角形的内部;③三角形的高有两条在三角形的外部,还有一条在三角形的内部;④在△ABC中,如果点P是AC边的中点,则PB是△ABC的中线.其中正确的是(
)
A.①②④
B.①②③④
C.①④
D.①②
10.如图,△ABC中,AD是BC边上的高,AE,BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75°
B.80°
C.85°
D.90°
二.填空题(共8小题,3
8=24)
11.如图,AD是△ABC的一条中线,若BD=3,则BC=_______.
12.
如图,△ABC中BC边上的高是______,△ACD中CD边上的高是________,△BCE中BC边上的高是__________,
13.如图,AD,BE,CF是△ABC的三条角平分线,则∠1=________,∠3=________,∠ACB=2____________.
14.如图,AD是△ABC中BC边上的中线,若△ABC的面积为20
cm2,则△ACD的面积是_____________.
15.如图,在△ABC中,∠BAC=60°,∠ACE=40°,AD,CE是△ABC的角平分线,则∠DAC=__________,∠BCE=_________,∠ACB=__________.
16.如图,BD是△ABC的中线,若AB=8cm,AC=6cm,BC=6cm,则△ABD与△BCD的周长之差为________cm.
17.如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各结论中正确的是__________
(填序号)
①BA=2BF;②AE=BE;③∠ACE=∠ACB;④CD⊥BE。
18.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E.若BC=10,AC=8,BE=5,则AD的长为____.
三.解答题(共7小题,
46分)
19.(6分)
如图,AD是∠CAB的平分线,
DF∥AC,EF交AD于点O,DO是∠EDF的平分线。求证:DE∥AB.
20.(6分)
如图,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高;
(2)若△ABD的面积为6,且BD边上的高为3,求BC的长.
21.(6分)
如图,AD是△ABC的角平分线,DE∥AC交AB于E,∠1=∠2,则DF与AB有什么关系?并说明理由.
22.(6分)
如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,且S△ABC
=4cm2,求则S阴影.
23.(6分)
等腰三角形一腰上的中线把该三角形的周长分为13.5和11.5两部分,求这个等腰三角形各边的长.
24.(8分)
如图,在△ABC中,AB>BC,AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
25.(8分)
如图所示,已知AD,AE分别是△ABC的高和中线,AB=6
cm,AC=8
cm,BC=10
cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
参考答案
1-5BCDBA
6-10ACDAA
11.
6
12.
AD,AD,BE
13.
∠2,∠ABC
,∠4(∠ACF)
14.
10
cm2
15.
30°,40°,80°
16.
2
17.
①③④
18.
4
19.
证明:∵DF∥AC,∴∠FDA=∠EAD.
∵AD是∠CAB的平分线,∴∠EAD=∠FAD.
∴∠FAD=∠FDA.
∵DO是∠EDF的平分线,∴∠EDA=∠FDA.
∴∠EDA=∠FAD.
∴DE∥AB.
20.
解:(1)如图所示.
(2)∵AD是△ABC的边BC上的中线,△ABD的面积为6,
∴△ABC的面积为12.
∵BD边上的高为3,
∴BC=12×2÷3=8.
21.
解:DF∥AB.理由:
∵DE∥AC,∴∠1=∠4,
∵AD是△ABC角平分线,∴∠3=∠4,∴∠1=∠3,
又∵∠1=∠2,∴∠2=∠3,
∴DF∥AB
22.
解:∵点D是BC的中点,∴BD=CD.∴S△ABD=S△ACD=S△ABC.
同理,S△BDE
=S△ABE=S△ABD,
S△CDE=S△ACE=S△ACD.
∴S△BCE=S△BDE+
S△CDE=(S△ABD+
S△ACD)=S△ABC=×4=2(cm2).
∵点F是CE的中点,∴S阴影=S△BEF=S△BCE=1(cm2).
23.
解:设在△ABC中,AB=AC,BD是AC边上的中线.
依题意,当AB>BC时,AB-BC=13.5-11.5=2,则AB=BC+2.
所以2(BC+2)+BC=13.5+11.5,
解得BC=7,则AB=AC=BC+2=9.
当AB
所以2AB+AB+2=13.5+11.5,
解得AB=,则AC=,BC=AB+2=.
综上,这个等腰三角形三边的长分别为9,9,7或,,.
24.
解:∵AD是BC边上的中线,∴BD=CD.设BD=CD=x,AB=y.
∵AC=2BC,∴AC=4x.分为两种情况:
①AC+CD=60,AB+BD=40,
则4x+x=60,x+y=40,
解得x=12,y=28,
即AC=4x=48,AB=28;
②AC+CD=40,AB+BD=60,
则4x+x=40,x+y=60,
解得x=8,y=52,
即AC=4x=32,AB=52,BC=2x=16,
此时不符合三角形三边关系.
综上所述,AC=48,AB=28
25.
解:(1)∵∠BAC=90°,AD
是边BC上的高,∴AB·AC=BC·AD,
∴AD===4.8(cm),即AD的长为4.8
cm.
(2)∵△ABC是直角三角形,∠BAC=90°,AB=6
cm,AC=8
cm,
∴S△ABC=AB·AC=×6×8=24(cm2).
又∵AE是△ABC的中线,∴BE=EC,
∴BE·AD=EC·AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12
cm2.∴△ABE的面积是12
cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是2
cm.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
