人教版八年级数学上册 11.2.1三角形的内角课后练习(含答案)
文档属性
| 名称 | 人教版八年级数学上册 11.2.1三角形的内角课后练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 00:00:00 | ||
图片预览

文档简介
人教版八年级数学上册
第十一章三角形
11.2.1三角形的内角
课后练习
一、单选题
1.如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118°
B.119°
C.120°
D.121°
2.如图,三角形的顶点落在折叠后的四边形内部,则∠γ与∠α+∠β之间的关系是(
)
A.∠γ=∠α+∠β
B.2∠γ=∠α+∠β
C.3∠γ=2∠α+∠β
D.3∠γ=2(α∠+∠β)
3.如图所示,∠A+∠B+∠C+∠D+∠E=
A.180°
B.260°
C.270°
D.360°
4.如图,BC⊥AE,垂足为C,过C作CD∥AB,若∠ECD=43°,则∠B=(
)
A.43°
B.57°
C.47°
D.45°
5.如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
A.24°
B.25°
C.30°
D.36°
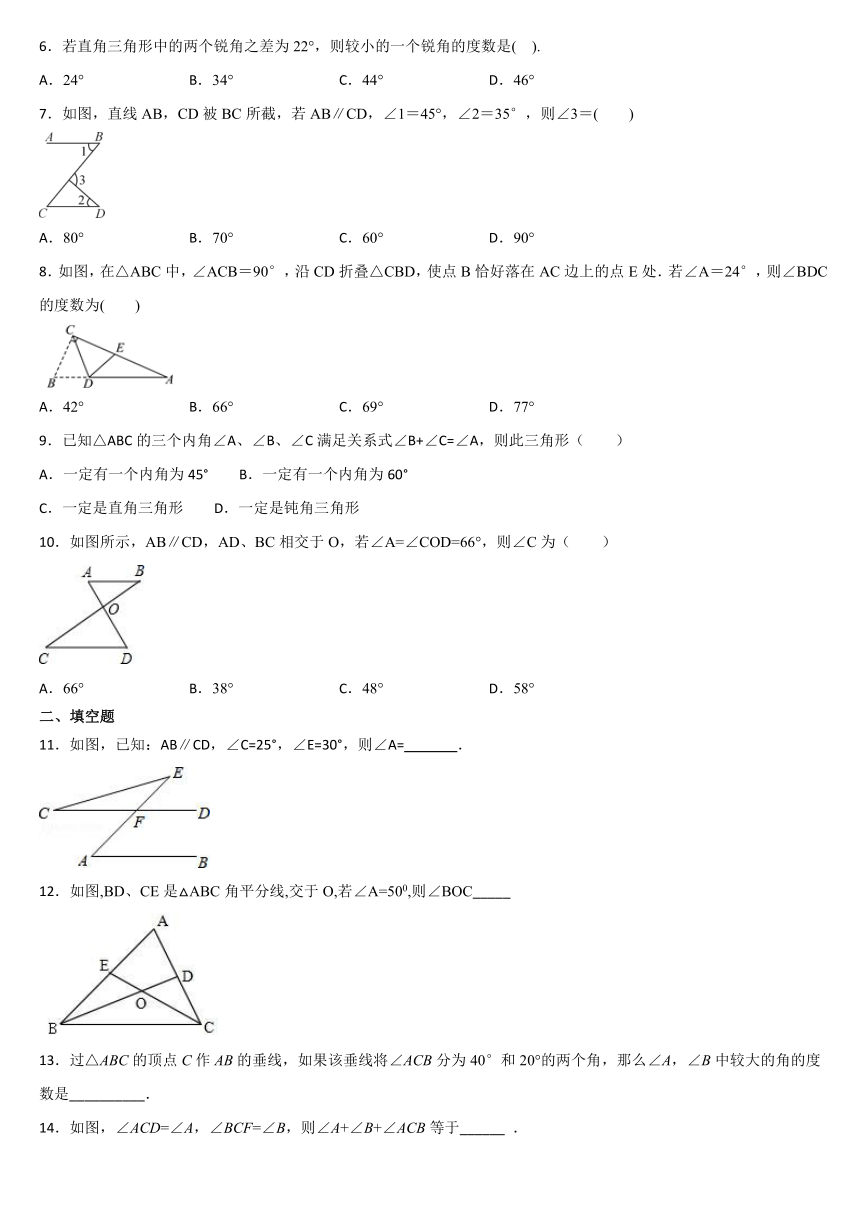
6.若直角三角形中的两个锐角之差为22°,则较小的一个锐角的度数是(
).
A.24°
B.34°
C.44°
D.46°
7.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=(
)
A.80°
B.70°
C.60°
D.90°
8.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC的度数为( )
A.42°
B.66°
C.69°
D.77°
9.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形( )
A.一定有一个内角为45°
B.一定有一个内角为60°
C.一定是直角三角形
D.一定是钝角三角形
10.如图所示,AB∥CD,AD、BC相交于O,若∠A=∠COD=66°,则∠C为( )
A.66°
B.38°
C.48°
D.58°
二、填空题
11.如图,已知:AB∥CD,∠C=25°,∠E=30°,则∠A=
.
12.如图,BD、CE是△ABC角平分线,交于O,若∠A=500,则∠BOC_____
13.过△ABC的顶点C作AB的垂线,如果该垂线将∠ACB分为40°和20°的两个角,那么∠A,∠B中较大的角的度数是__________.
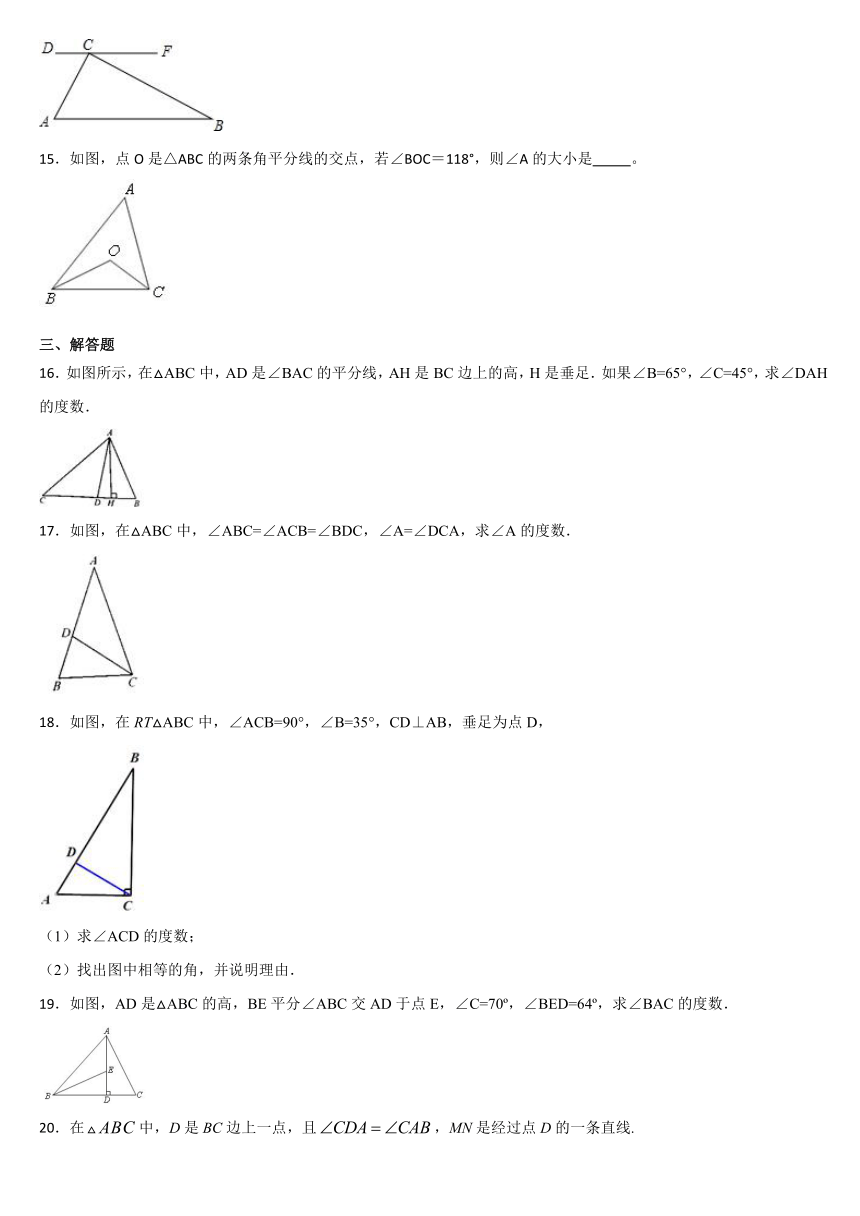
14.如图,∠ACD=∠A,∠BCF=∠B,则∠A+∠B+∠ACB等于______
.
15.如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是
。
三、解答题
16.如图所示,在△ABC中,AD是∠BAC的平分线,AH是BC边上的高,H是垂足.如果∠B=65°,∠C=45°,求∠DAH的度数.
17.如图,在△ABC中,∠ABC=∠ACB=∠BDC,∠A=∠DCA,求∠A的度数.
18.如图,在RT△ABC中,∠ACB=90°,∠B=35°,CD⊥AB,垂足为点D,
(1)求∠ACD的度数;
(2)找出图中相等的角,并说明理由.
19.如图,AD是△ABC的高,BE平分∠ABC交AD于点E,∠C=70?,∠BED=64?,求∠BAC的度数.
20.在中,D是BC边上一点,且,MN是经过点D的一条直线.
(1)若直线,垂足为点E.
①依题意补全图1.
②若,则________,________.
(2)如图2,若直线MN交AC边于点F,且,求证:.
【参考答案】
1.C
2.B
3.A
4.C
5.B
6.B
7.A
8.C
9.C
10.C
11.55°。
12.115°
13.70°
14.180°
15.56°
16.解:∵∠B=65°,∠C=45°,∠B+∠C+∠CAB=180°,
∴∠CAB=70°,
∵AD是∠BAC的平分线,
∴∠CAD=∠BAD=35°.
∵AH是BC边上的高,H是垂足,
∴∠AHB=90°.
∵∠B+∠AHB+∠BAH=180°,
∴∠BAH=25°,
∴∠DAH=10°.
17.解:∵∠A=∠DCA,
∴∠BDC=2∠A,
∵∠ABC=∠ACB=∠BDC,
∴∠ABC=∠ACB=2∠A,
∵∠ABC+∠ACB+∠A=180°,
∴2∠A+2∠A+∠A=180°,
∴5∠A=180°,
∴∠A=36°.
18.解:(1)在Rt△ABC中,∵∠ACB=90°,∠B=35°,
∴∠A=180°-90°-35°=55°,
∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠ACD=180°-90°-55°=35°;
(2))∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠BDC=∠ADC=∠ACB;
∵∠B=35°,∠ACD=35°,
∴∠B=∠ACD;
∵∠A=55°,∠BCD=∠ACB-∠ACD=90°-35°=55°,
∴∠A=∠BCD.
∴图中相等的角有:∠BDC=∠ADC=∠ACB,∠B=∠ACD,∠A=∠BCD.
19.∵AD是△ABC的高,∠C=70°,
∴∠DAC=20°,
∵BE平分∠ABC交AD于E,
∴∠ABE=∠EBD,
∵∠BED=64°,
∴∠ABE+∠BAE=64°,
∴∠EBD+64°=90°,
∴∠EBD=26°,
∴∠BAE=38°,
∴∠BAC=∠BAE+∠CAD=38°+20°=58°.
20.(1)①如图所示.
②,
.
,
.
,
.
故答案为.
(2),
且,
.
.
第十一章三角形
11.2.1三角形的内角
课后练习
一、单选题
1.如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118°
B.119°
C.120°
D.121°
2.如图,三角形的顶点落在折叠后的四边形内部,则∠γ与∠α+∠β之间的关系是(
)
A.∠γ=∠α+∠β
B.2∠γ=∠α+∠β
C.3∠γ=2∠α+∠β
D.3∠γ=2(α∠+∠β)
3.如图所示,∠A+∠B+∠C+∠D+∠E=
A.180°
B.260°
C.270°
D.360°
4.如图,BC⊥AE,垂足为C,过C作CD∥AB,若∠ECD=43°,则∠B=(
)
A.43°
B.57°
C.47°
D.45°
5.如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
A.24°
B.25°
C.30°
D.36°
6.若直角三角形中的两个锐角之差为22°,则较小的一个锐角的度数是(
).
A.24°
B.34°
C.44°
D.46°
7.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=(
)
A.80°
B.70°
C.60°
D.90°
8.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC的度数为( )
A.42°
B.66°
C.69°
D.77°
9.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A,则此三角形( )
A.一定有一个内角为45°
B.一定有一个内角为60°
C.一定是直角三角形
D.一定是钝角三角形
10.如图所示,AB∥CD,AD、BC相交于O,若∠A=∠COD=66°,则∠C为( )
A.66°
B.38°
C.48°
D.58°
二、填空题
11.如图,已知:AB∥CD,∠C=25°,∠E=30°,则∠A=
.
12.如图,BD、CE是△ABC角平分线,交于O,若∠A=500,则∠BOC_____
13.过△ABC的顶点C作AB的垂线,如果该垂线将∠ACB分为40°和20°的两个角,那么∠A,∠B中较大的角的度数是__________.
14.如图,∠ACD=∠A,∠BCF=∠B,则∠A+∠B+∠ACB等于______
.
15.如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是
。
三、解答题
16.如图所示,在△ABC中,AD是∠BAC的平分线,AH是BC边上的高,H是垂足.如果∠B=65°,∠C=45°,求∠DAH的度数.
17.如图,在△ABC中,∠ABC=∠ACB=∠BDC,∠A=∠DCA,求∠A的度数.
18.如图,在RT△ABC中,∠ACB=90°,∠B=35°,CD⊥AB,垂足为点D,
(1)求∠ACD的度数;
(2)找出图中相等的角,并说明理由.
19.如图,AD是△ABC的高,BE平分∠ABC交AD于点E,∠C=70?,∠BED=64?,求∠BAC的度数.
20.在中,D是BC边上一点,且,MN是经过点D的一条直线.
(1)若直线,垂足为点E.
①依题意补全图1.
②若,则________,________.
(2)如图2,若直线MN交AC边于点F,且,求证:.
【参考答案】
1.C
2.B
3.A
4.C
5.B
6.B
7.A
8.C
9.C
10.C
11.55°。
12.115°
13.70°
14.180°
15.56°
16.解:∵∠B=65°,∠C=45°,∠B+∠C+∠CAB=180°,
∴∠CAB=70°,
∵AD是∠BAC的平分线,
∴∠CAD=∠BAD=35°.
∵AH是BC边上的高,H是垂足,
∴∠AHB=90°.
∵∠B+∠AHB+∠BAH=180°,
∴∠BAH=25°,
∴∠DAH=10°.
17.解:∵∠A=∠DCA,
∴∠BDC=2∠A,
∵∠ABC=∠ACB=∠BDC,
∴∠ABC=∠ACB=2∠A,
∵∠ABC+∠ACB+∠A=180°,
∴2∠A+2∠A+∠A=180°,
∴5∠A=180°,
∴∠A=36°.
18.解:(1)在Rt△ABC中,∵∠ACB=90°,∠B=35°,
∴∠A=180°-90°-35°=55°,
∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠ACD=180°-90°-55°=35°;
(2))∵CD⊥AB,
∴∠BDC=∠ADC=90°,
∴∠BDC=∠ADC=∠ACB;
∵∠B=35°,∠ACD=35°,
∴∠B=∠ACD;
∵∠A=55°,∠BCD=∠ACB-∠ACD=90°-35°=55°,
∴∠A=∠BCD.
∴图中相等的角有:∠BDC=∠ADC=∠ACB,∠B=∠ACD,∠A=∠BCD.
19.∵AD是△ABC的高,∠C=70°,
∴∠DAC=20°,
∵BE平分∠ABC交AD于E,
∴∠ABE=∠EBD,
∵∠BED=64°,
∴∠ABE+∠BAE=64°,
∴∠EBD+64°=90°,
∴∠EBD=26°,
∴∠BAE=38°,
∴∠BAC=∠BAE+∠CAD=38°+20°=58°.
20.(1)①如图所示.
②,
.
,
.
,
.
故答案为.
(2),
且,
.
.
