【数学】3-4《函数的应用ⅱ》课件(新人教b版必修1)
文档属性
| 名称 | 【数学】3-4《函数的应用ⅱ》课件(新人教b版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 391.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
例1 我国人口总数是12亿,如果人口的年自然增长率为1.25%,问哪一年我国人口总数将超过14亿?
例2:
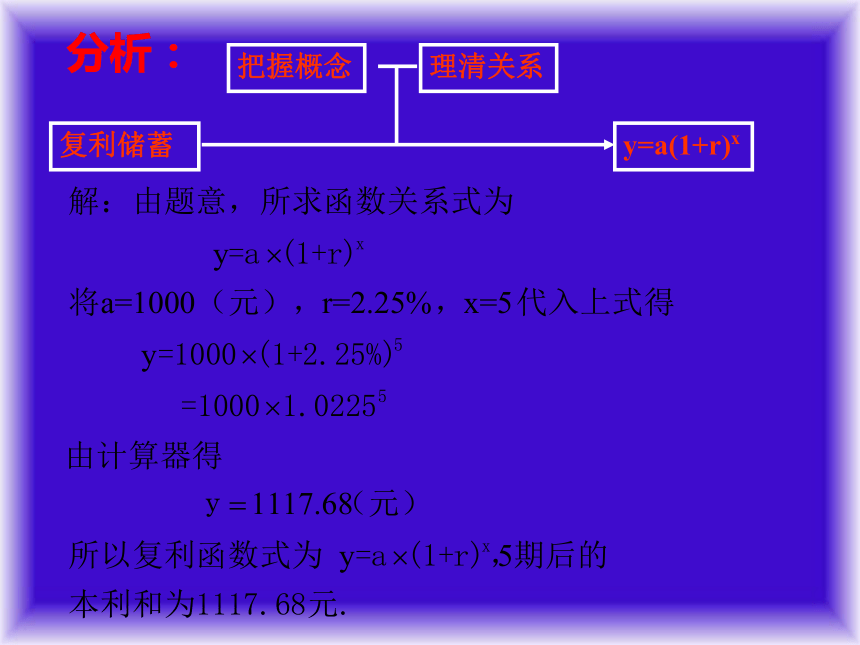
按复利计算利息的一种储蓄,本金为a元,每期利率为r,设本利和为y,存期为x.
(1)试写出本利和y 随存期x 变化的函数关系式.
(2)如果存入本金1000元,每期利率为2.25%,
试计算5期后本利和是多少(精确到0.01元)?
复利是一种计算利息的方法,即
把前一期的利息和本金加在一起算做
本金,再计算下一期的利息。
小知识:
分析:
把握概念
复利储蓄
理清关系
y=a(1+r)x
1、湖南华泰集团今年生产新闻纸a吨,在今后的8年内,计划使年产量平均每年比上一年增加P%,写出年产量随经过年数变化的函数关系式.
练一练:
解:设年产量经过x年增加到y件,
解:设成本经过x年降低到y元,
2、湖南凯银集团生产的牛肉成本每公斤a元,在今后6年内,计划使每公斤成本平均每年比上一年降低P%,写出成本随经过年数变化的函数关系式.
y=a(1+P%)x
(x∈N*且x≤8)
y=a(1-P%)x
(x∈N*且x≤6)
增长率问题的函数模型
如果原来的基础数为N,平均增长率为
p%,则关于时间x的总量y可表示为:
总量
基础数
平均增长率
时间
y=N(1+p%)x
趣味题
某商品降价20%后,欲恢复原价,
则应提价多少???
X= 25 %
引申:
某商品升价25%后,欲恢复原价,
则应降价多少???
X= 20 %
2.某工厂的一种产品的年产量第二年比
第一年增加 ,第三年比第二年增加
,则这两年的平均增长率是 .
32 %
3.某商场进了A、B两套服装, A提价
后以96元卖出, B降价 后以96元卖
出,则这两套服装销售后( )
A.不赚不亏 B. 赚了80元
C.亏了80元 D.赚了2000元
C
小
结
函数应用题的解题步骤可以用下面的框图表示:
数学模型的解
实际应用问题
数学模型
实际问题的解
抽象概括
还原说明
推理演算
数学模型就是把实际问题用数学语言抽象概括
,再从数学角度来反映或近似地反映实际问题
时,所得出所得出的关于实际问题的数学描述。
小结:解答应用题的基本步骤:
(1)合理、恰当假设 ;
(2)抽象概括数量关系,并能用数学语言表示;
(3) 分析、解决数学问题;
(4)数学问题的解向实际问题的还原。
作业:P115
习题3-4 A组 1,3,5
例1 我国人口总数是12亿,如果人口的年自然增长率为1.25%,问哪一年我国人口总数将超过14亿?
例2:
按复利计算利息的一种储蓄,本金为a元,每期利率为r,设本利和为y,存期为x.
(1)试写出本利和y 随存期x 变化的函数关系式.
(2)如果存入本金1000元,每期利率为2.25%,
试计算5期后本利和是多少(精确到0.01元)?
复利是一种计算利息的方法,即
把前一期的利息和本金加在一起算做
本金,再计算下一期的利息。
小知识:
分析:
把握概念
复利储蓄
理清关系
y=a(1+r)x
1、湖南华泰集团今年生产新闻纸a吨,在今后的8年内,计划使年产量平均每年比上一年增加P%,写出年产量随经过年数变化的函数关系式.
练一练:
解:设年产量经过x年增加到y件,
解:设成本经过x年降低到y元,
2、湖南凯银集团生产的牛肉成本每公斤a元,在今后6年内,计划使每公斤成本平均每年比上一年降低P%,写出成本随经过年数变化的函数关系式.
y=a(1+P%)x
(x∈N*且x≤8)
y=a(1-P%)x
(x∈N*且x≤6)
增长率问题的函数模型
如果原来的基础数为N,平均增长率为
p%,则关于时间x的总量y可表示为:
总量
基础数
平均增长率
时间
y=N(1+p%)x
趣味题
某商品降价20%后,欲恢复原价,
则应提价多少???
X= 25 %
引申:
某商品升价25%后,欲恢复原价,
则应降价多少???
X= 20 %
2.某工厂的一种产品的年产量第二年比
第一年增加 ,第三年比第二年增加
,则这两年的平均增长率是 .
32 %
3.某商场进了A、B两套服装, A提价
后以96元卖出, B降价 后以96元卖
出,则这两套服装销售后( )
A.不赚不亏 B. 赚了80元
C.亏了80元 D.赚了2000元
C
小
结
函数应用题的解题步骤可以用下面的框图表示:
数学模型的解
实际应用问题
数学模型
实际问题的解
抽象概括
还原说明
推理演算
数学模型就是把实际问题用数学语言抽象概括
,再从数学角度来反映或近似地反映实际问题
时,所得出所得出的关于实际问题的数学描述。
小结:解答应用题的基本步骤:
(1)合理、恰当假设 ;
(2)抽象概括数量关系,并能用数学语言表示;
(3) 分析、解决数学问题;
(4)数学问题的解向实际问题的还原。
作业:P115
习题3-4 A组 1,3,5
