人教版数学九年下册28.2 解直角三角形及其应用课件(第1课时 共19张PPT)
文档属性
| 名称 | 人教版数学九年下册28.2 解直角三角形及其应用课件(第1课时 共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 761.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 11:29:38 | ||
图片预览


文档简介
(共19张PPT)
人教版义务教育教材
数
学
(九年级下)
28.2.1
解直角三角形
学习目标
1、了解什么是解直角三角形;
2、会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.
知
识回
顾
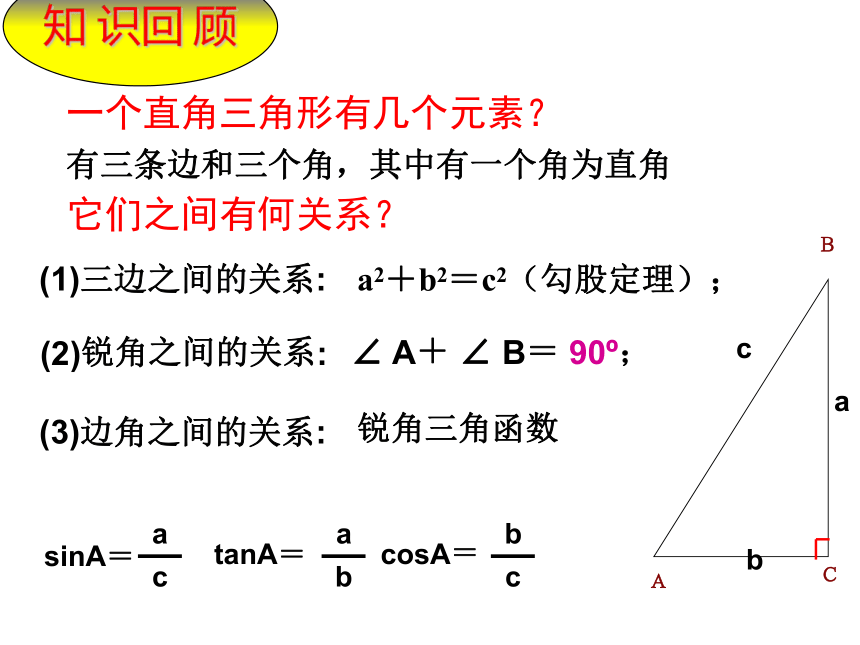
一个直角三角形有几个元素?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠
A+
∠
B=
90?;
(3)边角之间的关系:
sinA=
cosA=
tanA=
有三条边和三个角,其中有一个角为直角
锐角三角函数
它们之间有何关系?
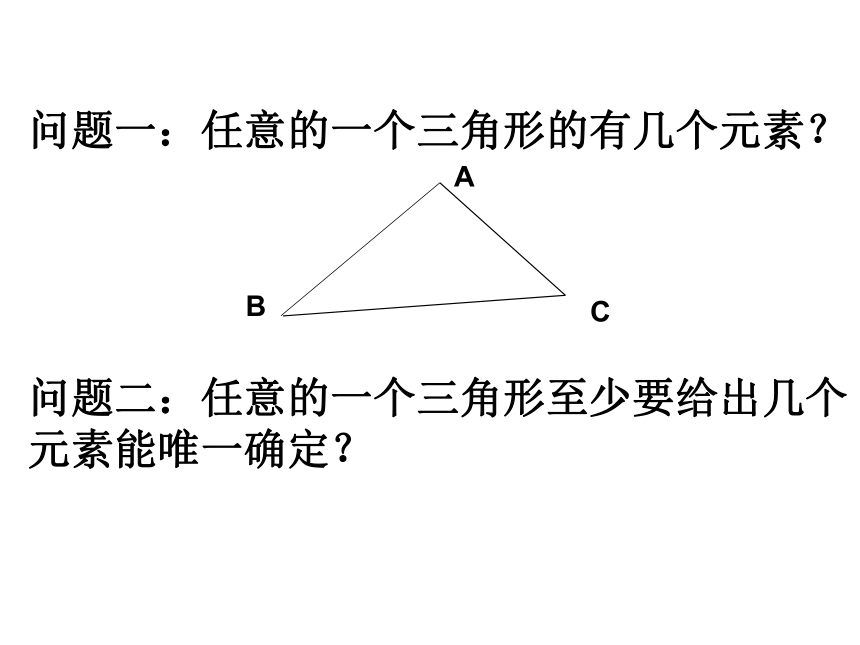
问题一:任意的一个三角形的有几个元素?
A
B
C
问题二:任意的一个三角形至少要给出几个元素能唯一确定?
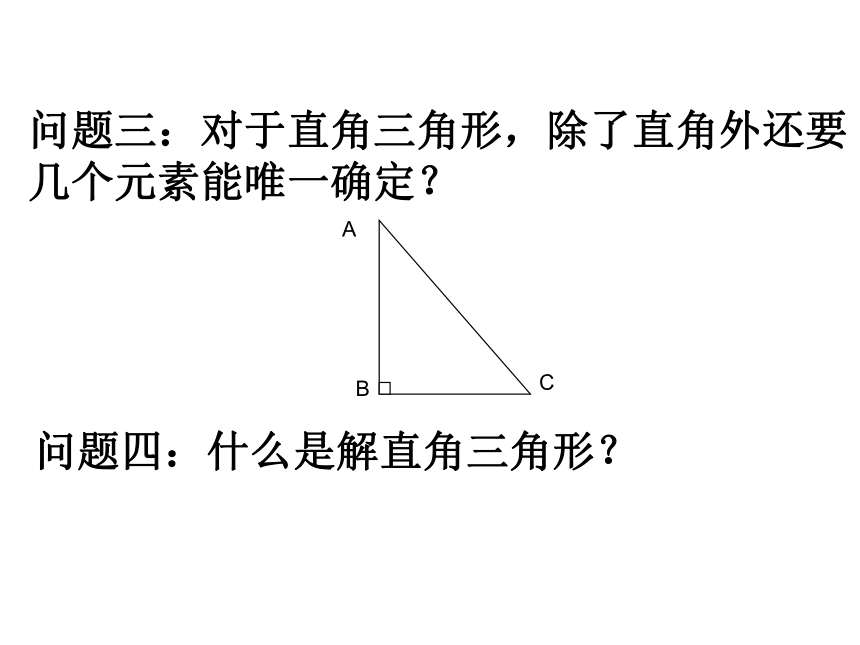
问题三:对于直角三角形,除了直角外还要几个元素能唯一确定?
A
B
C
问题四:什么是解直角三角形?
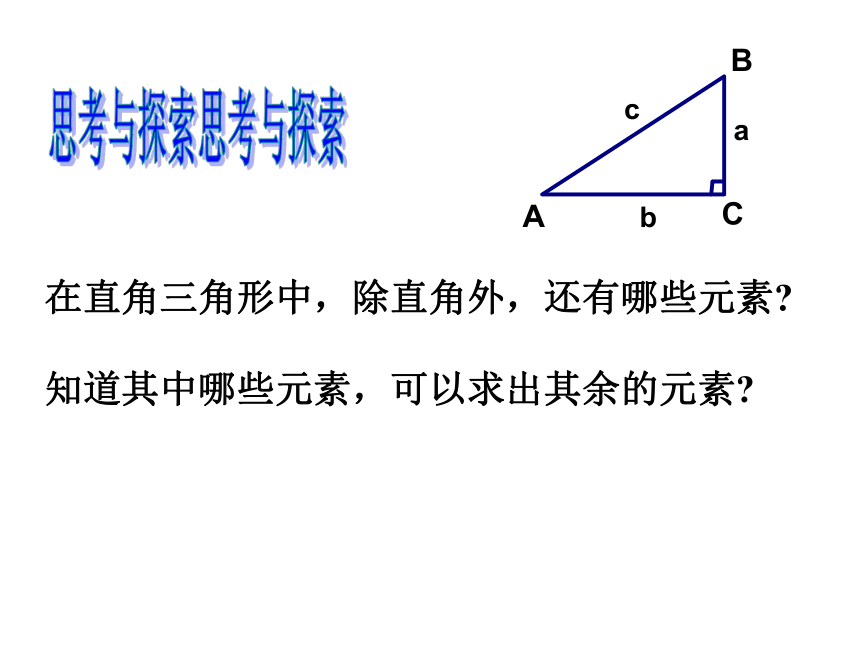
在直角三角形中,除直角外,还有哪些元素?
知道其中哪些元素,可以求出其余的元素?
思考与探索
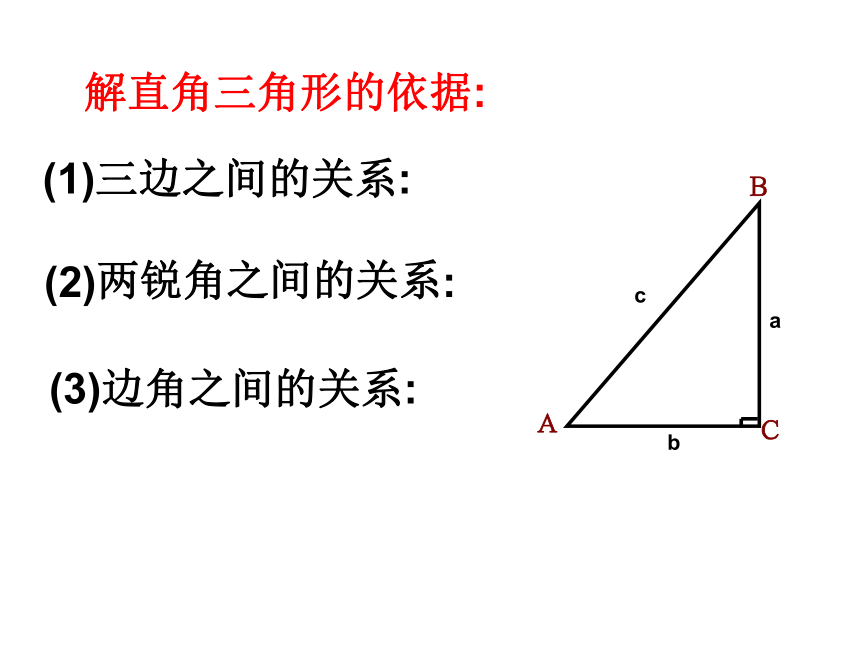
解直角三角形的依据:
(1)三边之间的关系:
(2)两锐角之间的关系:
(3)边角之间的关系:
在Rt△ABC中,
(1)根据∠A=
60°,斜边AB=30,
你能求出这个三角形的其他元素吗?
A
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
你发现了什么
B
C
∠B
AC
BC
∠A
∠B
AB
一角一边
两边
两角
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元
素吗?
不能
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠
A+
∠
B=
90?;
(3)边角之间的关系:
sinA=
cosA=
tanA=
锐角三角函数
在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形
解直角三角形的依据
例1
解:由勾股定理得:
在Rt
△ABC中,AB=2AC
所以,
∠B=30°
∠A=60°
?
基础练习
1、在下列直角三角形中不能求解的是(
)
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边
D、已知两角
2、Rt△ABC中,
∠C=90°,若sinA=
,AB=10,那么BC=_____,tanB=______.
D
8
基础练习
3.在Rt△ABC中,∠C=90°,a、b、c分别为
∠A
、∠B、
∠C的对边.根据已知条件,
解直角三角形.
(1)c=8,∠A
=60°;
(4)a=1,
∠B=30°.
在⊿ABC中,∠C=900,
解直角三角形:(如图)
C
A
B
4.已知a,c.则通过
,求
∠A
已知∠A,a.
则b=
,c=
;
3.已知∠A,b.
则a=
,
c=
.
2.已知∠A,c.
则a=
,b=
;
提高练习
5.已知a,b.则通过
,求
∠A
D
应用
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
试一试
变式
∠A+
∠
B=90°
a2+b2=c2
三角函数
关系式
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
人教版义务教育教材
数
学
(九年级下)
28.2.1
解直角三角形
学习目标
1、了解什么是解直角三角形;
2、会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.
知
识回
顾
一个直角三角形有几个元素?
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠
A+
∠
B=
90?;
(3)边角之间的关系:
sinA=
cosA=
tanA=
有三条边和三个角,其中有一个角为直角
锐角三角函数
它们之间有何关系?
问题一:任意的一个三角形的有几个元素?
A
B
C
问题二:任意的一个三角形至少要给出几个元素能唯一确定?
问题三:对于直角三角形,除了直角外还要几个元素能唯一确定?
A
B
C
问题四:什么是解直角三角形?
在直角三角形中,除直角外,还有哪些元素?
知道其中哪些元素,可以求出其余的元素?
思考与探索
解直角三角形的依据:
(1)三边之间的关系:
(2)两锐角之间的关系:
(3)边角之间的关系:
在Rt△ABC中,
(1)根据∠A=
60°,斜边AB=30,
你能求出这个三角形的其他元素吗?
A
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),就可以求出其余三个元素.
你发现了什么
B
C
∠B
AC
BC
∠A
∠B
AB
一角一边
两边
两角
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元
素吗?
不能
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠
A+
∠
B=
90?;
(3)边角之间的关系:
sinA=
cosA=
tanA=
锐角三角函数
在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形
解直角三角形的依据
例1
解:由勾股定理得:
在Rt
△ABC中,AB=2AC
所以,
∠B=30°
∠A=60°
?
基础练习
1、在下列直角三角形中不能求解的是(
)
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边
D、已知两角
2、Rt△ABC中,
∠C=90°,若sinA=
,AB=10,那么BC=_____,tanB=______.
D
8
基础练习
3.在Rt△ABC中,∠C=90°,a、b、c分别为
∠A
、∠B、
∠C的对边.根据已知条件,
解直角三角形.
(1)c=8,∠A
=60°;
(4)a=1,
∠B=30°.
在⊿ABC中,∠C=900,
解直角三角形:(如图)
C
A
B
4.已知a,c.则通过
,求
∠A
已知∠A,a.
则b=
,c=
;
3.已知∠A,b.
则a=
,
c=
.
2.已知∠A,c.
则a=
,b=
;
提高练习
5.已知a,b.则通过
,求
∠A
D
应用
求解非直角三角形的边角问题,常通过添加适当的辅助线,将其转换为直角三角形来解.
试一试
变式
∠A+
∠
B=90°
a2+b2=c2
三角函数
关系式
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
