江苏省泰州市2019-2020学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 江苏省泰州市2019-2020学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-10 15:35:37 | ||
图片预览



文档简介
泰州市10579100124460002019-2020学年度第二学期期末考试
高一数学试题
一、单项选择题
1.已知false中,false,false,false,则false的面积为( )
A.3 B.false C.false D.6
2.点false在空间直角坐标系false中的位置是( )
A.在false轴上 B.在false平面内
C.在false平面内 D.在false平面内
3.甲、乙、丙三位同学排成一列,甲乙两人相邻的概率为( )
A.false B.false C.false D.false
4.已知圆锥的轴截面是边长为2的等边三角形,则该圆锥的侧面积为( )
A.false B.false C.false D.false
5.已知正三棱柱false中,false,则点false到平面false的距离等于( )
A.1 B.false C.false D.false
6.如果false,false,…,false的方差为2,则false,false,…,false的方差为( )
A.2 B.4 C.8 D.16
7.在四棱锥false中,底面false为正方形,false平面false,false,则异面直线false与false所成角的大小为( )
A.false B.false C.false D.false
8.在平面直角坐标系false中,过点false向圆false:false引切线,切线长为false.设点false到直线false的距离为false,当false取最小值时,false的值为( )
A.false B.3 C.false D.4
二、多项选择题
9.从装有大小和形状完全相同的2个红球和3个黑球的口袋内任取2个球,下列各对事件中,互斥而不对立的是( )
A.“至少一个红球”和“都是红球”
B.“恰有一个红球”和“都是红球”
C.“恰有一个红球”和“都是黑球”
D.“至少一个红球”和“都是黑球”
10.当实数false变化时,圆false与圆false的位置关系可能是( )
A.外离 B.外切 C.相交 D.内含
11.false中,false,false,则下列叙述正确的是( )
A.false的外接圆的直径为4
B.若false,则满足条件的false有且只有1个
C.若满足条件的false有且只有1个,则false
D.若满足条件的false有两个,则false
12.已知四边形false是边长为1的正方形,将其沿着对角线false折成四面体false,则( )
A.false
B.四面体false的外接球的表面积为false
C.四面体false体积的最大值为false
D.直线false与直线false不可能垂直
三、填空题
13.已知随机事件false,false互斥,且false,false,则false______.
14.已知正六棱锥的底面面积为false,侧棱长为false,则这个棱锥的体积为______.
15.公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下结论:平面内到两定点距离之比等于已知数的动点轨迹为直线或圆.后世把这种圆称之为阿波罗尼斯圆.已知平面直角坐标系中,false,false,动点false满足false.
若点false的轨迹为一条直线,则false______;
若false,则点false的轨迹方程为______.
16.如图,在false中,角false的平分线交false于false,且false.若false,false,则false______.
四、解答题
17.(1)若直线false过点false,且与直线false平行,求直线false的方程;
(2)若点false与点false关于直线false对称,求点false的坐标.
18.如图,直四棱柱false中,四边形false是菱形.
(1)求证:false平面false;
(2)求证:false平面false.
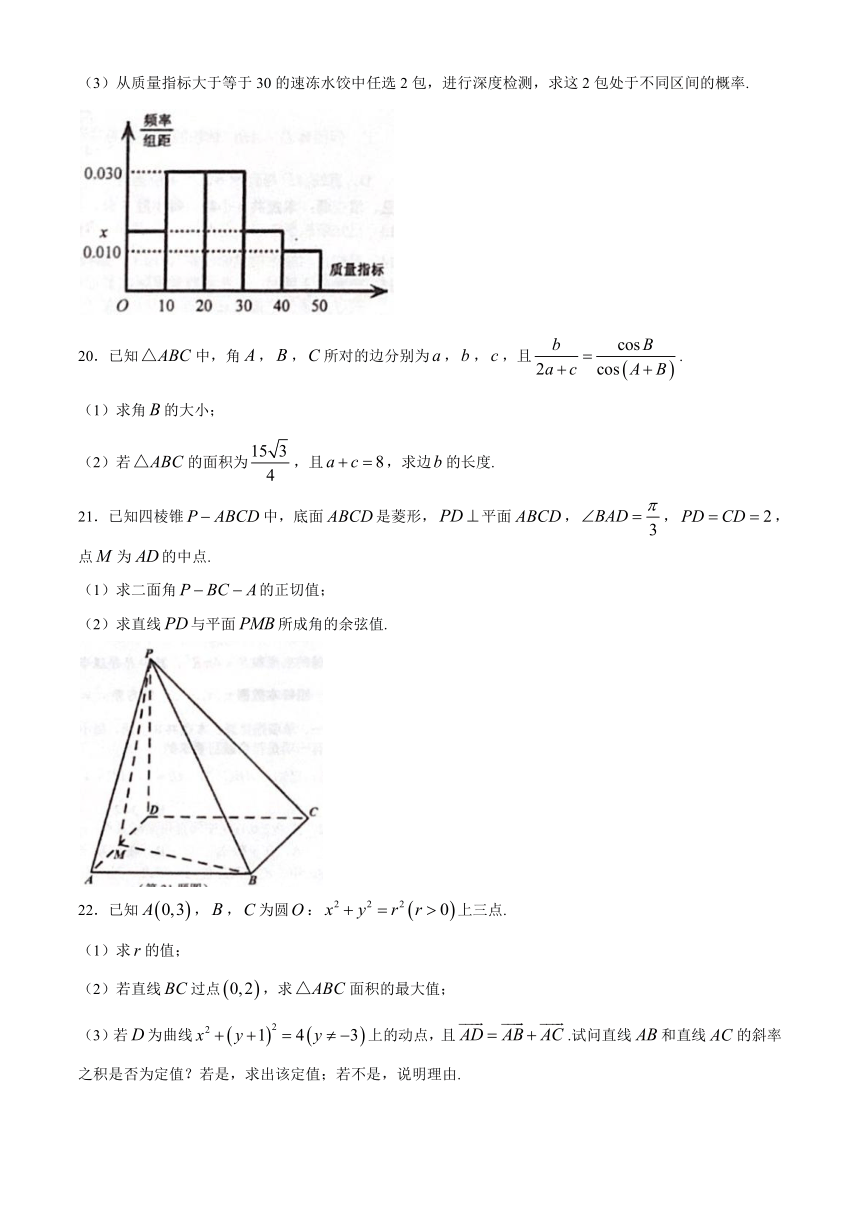
19.为了保证食品安全,保障公众身体健康和生命安全,2018年国家对《食品安全法》进行了修正.2020年春节前夕,某市质检部门随机抽取了20包某种品牌的速冻水饺,对某项质量指标进行检测.经统计,质量指标均在区间[0,50]内,将其按[0.10)、[10,20)、[20,30)、[30,40)、[40,50]分成5组,制成如图所示的频率分布直方图.
(1)求该频率分布直方图中false的值;
(2)若同组中的每个数据用该组区间中点值代替,估计该品牌速冻水饺的该项质量指标的平均值;
(3)从质量指标大于等于30的速冻水饺中任选2包,进行深度检测,求这2包处于不同区间的概率.
20.已知false中,角false,false,false所对的边分别为false,false,false,且false.
(1)求角false的大小;
(2)若false的面积为false,且false,求边false的长度.
21.已知四棱锥false中,底面false是菱形,false平面false,false,false,点false为false的中点.
(1)求二面角false的正切值;
(2)求直线false与平面false所成角的余弦值.
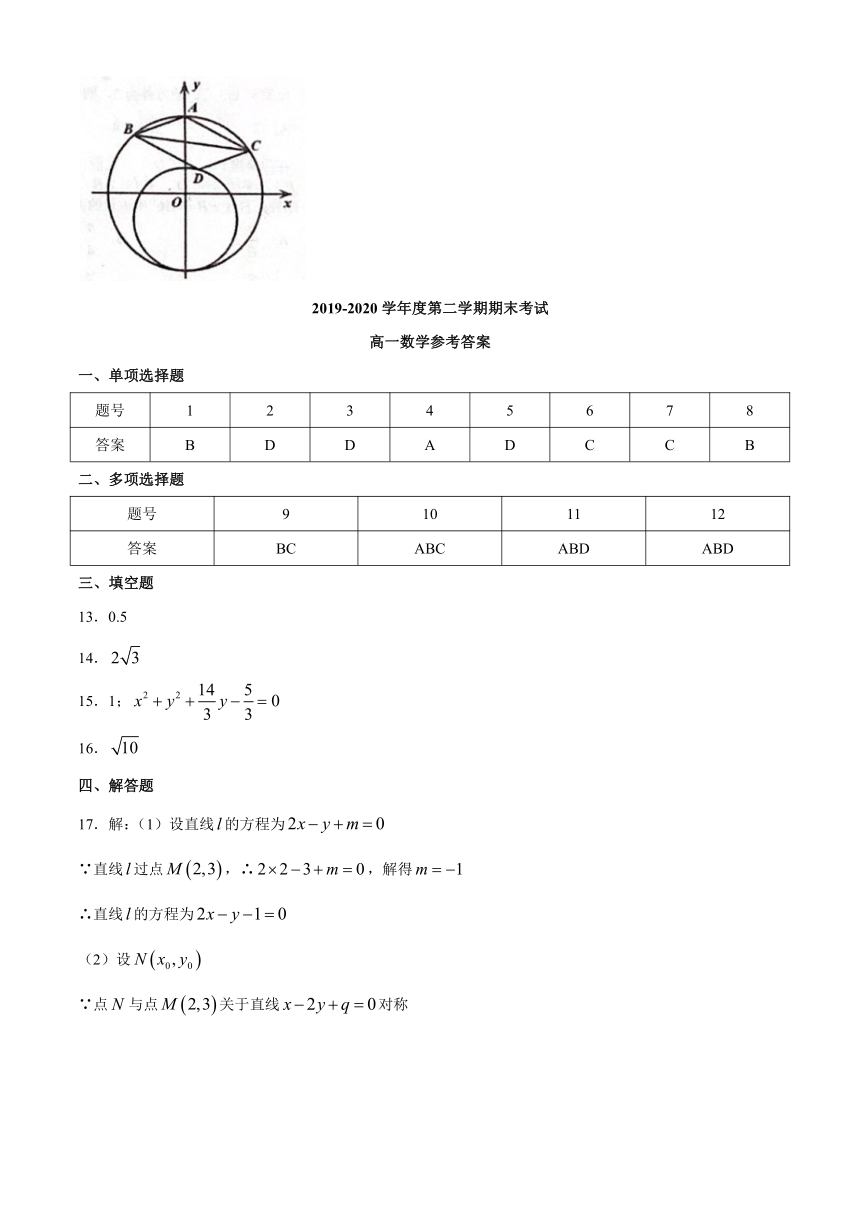
22.已知false,false,false为圆false:false上三点.
(1)求false的值;
(2)若直线false过点false,求false面积的最大值;
(3)若false为曲线false上的动点,且false.试问直线false和直线false的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
2019-2020学年度第二学期期末考试
高一数学参考答案
一、单项选择题
题号
1
2
3
4
5
6
7
8
答案
B
D
D
A
D
C
C
B
二、多项选择题
题号
9
10
11
12
答案
BC
ABC
ABD
ABD
三、填空题
13.0.5
14.false
15.1;false
16.false
四、解答题
17.解:(1)设直线false的方程为false
∵直线false过点false,∴false,解得false
∴直线false的方程为false
(2)设false
∵点false与点false关于直线false对称
∴false,解得false
故点false的坐标为false
18.证明:(1)∵false为四棱柱
∴侧面false为平行四边形,∴false
又false平面false,false平面false
∴false平面false
(2)∵false是直四棱柱
∴false平面false
又∵false平面false,∴false
∵false是菱形,∴false
又∵false平面false,false平面false,false
∴false平面false
19.解:(1)∵质量指标均在区间false内
∴false,∴false
∴该频率分布直方图中false的值为0.015
(2)各组的频率分别为0.15、0.3、0.3、0.15、0.1
各组区间中点值分别为5、15、25、35、45
∴平均值为false
∴估计该品牌速冻水饺的该项质量指标的平均值为22.5
(3)质量指标大于等于30包含两个区间[30,40)、[40,50],频数分别为3、2
在区间[30,40)内的3包速冻水饺分别记为false、false、false
在区间[40,50]内的2包速冻水饺分别记为false、false
从中任取2包,基本事件包含false、false、false、false、false、false、false、false、false、false,共10种
其中处于不同区间的事件(记为事件false)包含false、false、false、false、false、false,共6种
∴false
∴这2包处于不同区间的概率为false
20.解:(1)由正弦定理false,得false
∵false,∴false
整理得false,false
∵false,∴false,∴false
∵false,∴false
(2)∵false的面积为false
∴false,解得false
由余弦定理false,得false
∵false,∴false
21.解:(1)连结false,取false的中点false,连结false、false
∵false平面false,false平面false,false平面false
∴false,false
∵底面false是菱形,false
∴false,false为正三角形
∵false为false中点,false
∴false,false
∵false,false,false、false平面false,false
∴false平面false
∵false平面false,∴false
∵false,false,false平面false,false平面false
∴false为二面角false的平面角
∵false
∴在false中,false,false,false
∴false
∴二面角false的正切值为false
(2)∵底面false是菱形,false
∴false为正三角形
∵点false为false的中点,∴false
∵false平面false,false平面false
∴false
∵false,false,false、false平面false,false
∴false平面false
在平面false内过点false作false,交false于点false
∵false平面false,false平面false,∴false
∵false,false,false、false平面false,false
∴false平面false
∴false即为直线false与平面false所成角
∵false平面false,false平面false,∴false
∵底面false是菱形,false,点false为false的中点
∴false,false
false中false,false,false
∴false
∴false
22.解:(1)∵false为圆false上,∴false
(2)方法一:设直线false的方程为false,false,false
将false代入false得,false
false
令false,则false,false
当false,即false时,false面积取得最大值false
方法二:∵直线false过点false,∴false面积等于false面积的一半
设false到直线false的距离为false,则false
false
设false,则false
当false,即false时,false面积取得最大值false
(3)设直线false和直线false的斜率之积为false,
设false,false,false,则false
false①,false
因为false,false为圆false:false上,所以false,false
false,化简得false
整理得false②
因为false,所以false
从而false,又因为false为曲线false上的动点
所以false,展开得
false,将①代入得
false,化简得
false,将②代入得
false,整理得
false,
因为false,所以false,从而false
又false,所以false
高一数学试题
一、单项选择题
1.已知false中,false,false,false,则false的面积为( )
A.3 B.false C.false D.6
2.点false在空间直角坐标系false中的位置是( )
A.在false轴上 B.在false平面内
C.在false平面内 D.在false平面内
3.甲、乙、丙三位同学排成一列,甲乙两人相邻的概率为( )
A.false B.false C.false D.false
4.已知圆锥的轴截面是边长为2的等边三角形,则该圆锥的侧面积为( )
A.false B.false C.false D.false
5.已知正三棱柱false中,false,则点false到平面false的距离等于( )
A.1 B.false C.false D.false
6.如果false,false,…,false的方差为2,则false,false,…,false的方差为( )
A.2 B.4 C.8 D.16
7.在四棱锥false中,底面false为正方形,false平面false,false,则异面直线false与false所成角的大小为( )
A.false B.false C.false D.false
8.在平面直角坐标系false中,过点false向圆false:false引切线,切线长为false.设点false到直线false的距离为false,当false取最小值时,false的值为( )
A.false B.3 C.false D.4
二、多项选择题
9.从装有大小和形状完全相同的2个红球和3个黑球的口袋内任取2个球,下列各对事件中,互斥而不对立的是( )
A.“至少一个红球”和“都是红球”
B.“恰有一个红球”和“都是红球”
C.“恰有一个红球”和“都是黑球”
D.“至少一个红球”和“都是黑球”
10.当实数false变化时,圆false与圆false的位置关系可能是( )
A.外离 B.外切 C.相交 D.内含
11.false中,false,false,则下列叙述正确的是( )
A.false的外接圆的直径为4
B.若false,则满足条件的false有且只有1个
C.若满足条件的false有且只有1个,则false
D.若满足条件的false有两个,则false
12.已知四边形false是边长为1的正方形,将其沿着对角线false折成四面体false,则( )
A.false
B.四面体false的外接球的表面积为false
C.四面体false体积的最大值为false
D.直线false与直线false不可能垂直
三、填空题
13.已知随机事件false,false互斥,且false,false,则false______.
14.已知正六棱锥的底面面积为false,侧棱长为false,则这个棱锥的体积为______.
15.公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下结论:平面内到两定点距离之比等于已知数的动点轨迹为直线或圆.后世把这种圆称之为阿波罗尼斯圆.已知平面直角坐标系中,false,false,动点false满足false.
若点false的轨迹为一条直线,则false______;
若false,则点false的轨迹方程为______.
16.如图,在false中,角false的平分线交false于false,且false.若false,false,则false______.
四、解答题
17.(1)若直线false过点false,且与直线false平行,求直线false的方程;
(2)若点false与点false关于直线false对称,求点false的坐标.
18.如图,直四棱柱false中,四边形false是菱形.
(1)求证:false平面false;
(2)求证:false平面false.
19.为了保证食品安全,保障公众身体健康和生命安全,2018年国家对《食品安全法》进行了修正.2020年春节前夕,某市质检部门随机抽取了20包某种品牌的速冻水饺,对某项质量指标进行检测.经统计,质量指标均在区间[0,50]内,将其按[0.10)、[10,20)、[20,30)、[30,40)、[40,50]分成5组,制成如图所示的频率分布直方图.
(1)求该频率分布直方图中false的值;
(2)若同组中的每个数据用该组区间中点值代替,估计该品牌速冻水饺的该项质量指标的平均值;
(3)从质量指标大于等于30的速冻水饺中任选2包,进行深度检测,求这2包处于不同区间的概率.
20.已知false中,角false,false,false所对的边分别为false,false,false,且false.
(1)求角false的大小;
(2)若false的面积为false,且false,求边false的长度.
21.已知四棱锥false中,底面false是菱形,false平面false,false,false,点false为false的中点.
(1)求二面角false的正切值;
(2)求直线false与平面false所成角的余弦值.
22.已知false,false,false为圆false:false上三点.
(1)求false的值;
(2)若直线false过点false,求false面积的最大值;
(3)若false为曲线false上的动点,且false.试问直线false和直线false的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
2019-2020学年度第二学期期末考试
高一数学参考答案
一、单项选择题
题号
1
2
3
4
5
6
7
8
答案
B
D
D
A
D
C
C
B
二、多项选择题
题号
9
10
11
12
答案
BC
ABC
ABD
ABD
三、填空题
13.0.5
14.false
15.1;false
16.false
四、解答题
17.解:(1)设直线false的方程为false
∵直线false过点false,∴false,解得false
∴直线false的方程为false
(2)设false
∵点false与点false关于直线false对称
∴false,解得false
故点false的坐标为false
18.证明:(1)∵false为四棱柱
∴侧面false为平行四边形,∴false
又false平面false,false平面false
∴false平面false
(2)∵false是直四棱柱
∴false平面false
又∵false平面false,∴false
∵false是菱形,∴false
又∵false平面false,false平面false,false
∴false平面false
19.解:(1)∵质量指标均在区间false内
∴false,∴false
∴该频率分布直方图中false的值为0.015
(2)各组的频率分别为0.15、0.3、0.3、0.15、0.1
各组区间中点值分别为5、15、25、35、45
∴平均值为false
∴估计该品牌速冻水饺的该项质量指标的平均值为22.5
(3)质量指标大于等于30包含两个区间[30,40)、[40,50],频数分别为3、2
在区间[30,40)内的3包速冻水饺分别记为false、false、false
在区间[40,50]内的2包速冻水饺分别记为false、false
从中任取2包,基本事件包含false、false、false、false、false、false、false、false、false、false,共10种
其中处于不同区间的事件(记为事件false)包含false、false、false、false、false、false,共6种
∴false
∴这2包处于不同区间的概率为false
20.解:(1)由正弦定理false,得false
∵false,∴false
整理得false,false
∵false,∴false,∴false
∵false,∴false
(2)∵false的面积为false
∴false,解得false
由余弦定理false,得false
∵false,∴false
21.解:(1)连结false,取false的中点false,连结false、false
∵false平面false,false平面false,false平面false
∴false,false
∵底面false是菱形,false
∴false,false为正三角形
∵false为false中点,false
∴false,false
∵false,false,false、false平面false,false
∴false平面false
∵false平面false,∴false
∵false,false,false平面false,false平面false
∴false为二面角false的平面角
∵false
∴在false中,false,false,false
∴false
∴二面角false的正切值为false
(2)∵底面false是菱形,false
∴false为正三角形
∵点false为false的中点,∴false
∵false平面false,false平面false
∴false
∵false,false,false、false平面false,false
∴false平面false
在平面false内过点false作false,交false于点false
∵false平面false,false平面false,∴false
∵false,false,false、false平面false,false
∴false平面false
∴false即为直线false与平面false所成角
∵false平面false,false平面false,∴false
∵底面false是菱形,false,点false为false的中点
∴false,false
false中false,false,false
∴false
∴false
22.解:(1)∵false为圆false上,∴false
(2)方法一:设直线false的方程为false,false,false
将false代入false得,false
false
令false,则false,false
当false,即false时,false面积取得最大值false
方法二:∵直线false过点false,∴false面积等于false面积的一半
设false到直线false的距离为false,则false
false
设false,则false
当false,即false时,false面积取得最大值false
(3)设直线false和直线false的斜率之积为false,
设false,false,false,则false
false①,false
因为false,false为圆false:false上,所以false,false
false,化简得false
整理得false②
因为false,所以false
从而false,又因为false为曲线false上的动点
所以false,展开得
false,将①代入得
false,化简得
false,将②代入得
false,整理得
false,
因为false,所以false,从而false
又false,所以false
同课章节目录
