【数学】1.1.1《角的概念的推广》课件(1)(新人教b版必修4)
文档属性
| 名称 | 【数学】1.1.1《角的概念的推广》课件(1)(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 28.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 16:11:36 | ||
图片预览







文档简介
(共24张PPT)
角的概念扩展
1、角的概念
初中是如何定义角的?
从一个点出发引出的两条射线构成的几何图形.
这种概念的优点是形象、直观、容易理解,但它是从图形形状来定义角,因此角的范围是[0 , 360 ),
这种定义称为静态定义,其弊端在于“狭隘”.
生活中很多实例会不在该范围。
体操运动员转体720 ,跳水运动员向内、向外转体1080 ;
经过1小时,时针、分针、秒针各转了多少度?
这些例子不仅不在范围[0 , 360 ) ,而且方向不同,有必要将角的概念推广到任意角,
想想用什么办法才能推广到任意角?
关键是用运动的观点来看待角的变化。
2.角的概念的推广
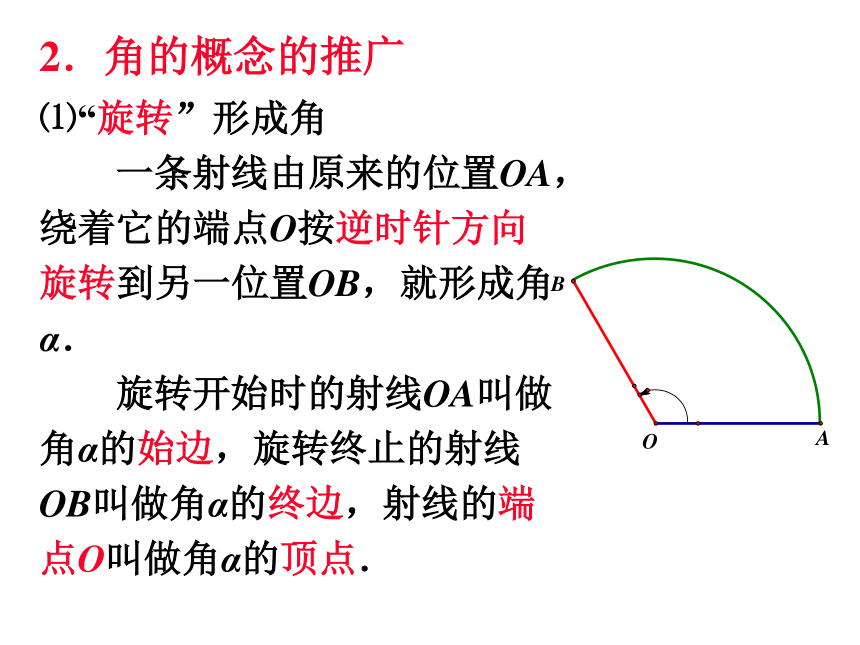
⑴“旋转”形成角
一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到另一位置OB,就形成角α.
旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB叫做角α的终边,射线的端点O叫做角α的顶点.
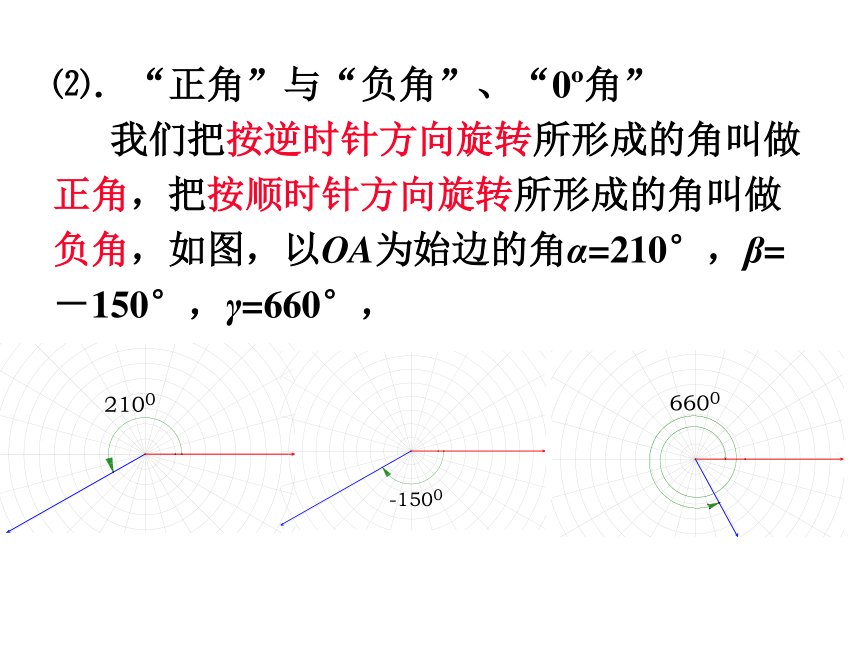
⑵.“正角”与“负角”、“0 角”
我们把按逆时针方向旋转所形成的角叫做正角,把按顺时针方向旋转所形成的角叫做负角,如图,以OA为始边的角α=210°,β=-150°,γ=660°,
特别地,当一条射线没有作任何旋转时,我们也认为这时形成了一个角,并把这个角叫做零度角(0 ).
角的记法:角α或可以简记成∠α.
⑶角的概念扩展的意义:
用“旋转”定义角之后,角的范围大大地扩大了
① 角有正负之分; 如: =210 , = 150 , =660 .
② 角可以任意大;
实例:体操动作:旋转2周(360 ×2=720 ) 3周(360 ×3=1080 )
③ 还有零角, 一条射线,没有旋转.
角的概念推广以后,它包括任意大小的正角、负角和零角.
要注意,正角和负角是表示具有相反意义的旋转量,它的正负规定纯属于习惯,就好象与正数、负数的规定一样,零角无正负,就好象数零无正负一样.
用旋转来描述角,需要注意三个要素(旋转中心、旋转方向和旋转量)
(2)旋转方向:旋转变换的方向分为逆时针和顺时针两种,这是一对意义相反的量,根据以往的经验,我们可以把一对意义相反的量用正负数来表示,那么许多问题就可以解决了;
(1)旋转中心:作为角的顶点.
(3)旋转量:
当旋转超过一周时,旋转量即超过360 ,角度的绝对值可大于360 .于是就会出现720 , - 540 等角度.
3.“象限角”
为了研究方便,我们往往在平面直角坐标系中来讨论角。
角的顶点重合于坐标原点,角的始边重合于x轴的正半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角(角的终边落在坐标轴上,则此角不属于任何一个象限)
例如:30 、390 、 330 是第Ⅰ象限角,
300 、 60 是第Ⅳ象限角,
585 、1300 是第Ⅲ象限角,
135 、 2000 是第Ⅱ象限角等
4.终边相同的角
⑴ 观察:390 , 330 角,它们的终边都与30 角的终边相同.
⑵探究:终边相同的角都可以表示成一个0 到360 的角与k(k∈Z)个周角的和:
390 =30 +360 (k=1), 330 =30 360 (k=-1)
30 =30 +0×360 (k=0), 1470 =30 +4×360 (k=4)
1770 =30 5×360 (k=-5)
⑶ 结论:
所有与 终边相同的角连同 在内可以构成一个集合:{β| β=α+k·360 }(k∈Z)
即:任何一个与角 终边相同的角,都可以表示成角 与整数个周角的和
⑷注意以下四点:
① k∈Z;
② 是任意角;
③ k·360 与 之间是“+”号,如k·360 -30 ,应看成k·360 +(-30 );
④ 终边相同的角不一定相等,但相等的角,终边一定相同,终边相同的角有无数多个,它们相差360 的整数倍.
例1. 在0 到360 范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角.
(1) -120 ;(2) 640 ;(3) -950 12′.
解:⑴∵-120 =-360 +240 ,
∴240 的角与-120 的角终边相同,
它是第三象限角.
⑵ ∵640 =360 +280 ,
∴280 的角与640 的角终边相同,
它是第四象限角.
⑶ ∵-950 12’=-3×360 +129 48’,
∴129 48’的角与-950 12’的角终边相同,
它是第二象限角.
例2. 写出与下列各角终边相同的角的集合S,并把S中在-360 ~720 间的角写出来:
(1) 60 ;(2) -21 ;(3) 363 14′.
解:(1) S={β| β=k·360 +60 (k∈Z) },
S中在-360 ~720 间的角是
-1×360 +60 =-280 ;
0×360 +60 =60 ;
1×360 +60 =420 .
(2) S={β| β=k·360 -21 (k∈Z) }
S中在-360 ~720 间的角是
0×360 -21 =-21 ;
1×360 -21 =339 ;
2×360 -21 =699 .
(3) β| β=k·360 + 363 14’ (k∈Z) }
S中在-360 ~720 间的角是
-2×360 +363 14’=-356 46’;
-1×360 +363 14’=3 14’;
0×360 +363 14’=363 14’.
课堂练习
1.锐角是第几象限的角?第一象限的角是否都是锐角?小于90 的角是锐角吗?区间(0 ,90 )内的角是锐角吗?
答:锐角是第一象限角;第一象限角不一定是锐角;小于90 的角可能是零角或负角,故它不一定是锐角;区间(0 ,90 )内的角是锐角.
2.已知角的顶点与坐标系原点重合,始边落在x轴的正半轴上,作出下列各角,并指出它们是哪个象限的角?
(1)420 ,(2) -75 ,(3)855 ,(4) -510 .
答:(1)第一象限角;
(2)第四象限角,
(3)第二象限角,
(4)第三象限角.
3、已知α,β角的终边相同,那么α-β的终边在( )
A x轴的非负半轴上 B y轴的非负半轴上
C x轴的非正半轴上 D y轴的非正半轴上
A
4、终边与坐标轴重合的角的集合是( )
A {β|β=k·360 (k∈Z) }
B {β|β=k·180 (k∈Z) }
C {β|β=k·90 (k∈Z) }
D {β|β=k·180 +90 (k∈Z) }
C
5 、已知角2α的终边在x轴的上方,那么α是( )
A 第一象限角 B 第一、二象限角
C 第一、三象限角 D 第一、四象限角
C
6、若α是第四象限角,则180 -α是( )
A 第一象限角 B 第二象限角
C 第三象限角 D 第四象限角
C
7、在直角坐标系中,若α与β终边互相垂直,那么α与β之间的关系是( )
A. β=α+90o
B β=α±90o
C β=k·360o+90o+α,k∈Z
D β=k·360o±90o+α, k∈Z
D
8、若90 <β<α<135 ,则α-β的范围是__________,α+β的范围是___________;
(0 ,45 )
(180 ,270 )
9、若β的终边与60 角的终边相同,那么在[0 ,360 ]范围内,终边与角 的终边相同的角为______________;
解:β=k·360 +60 ,k∈Z.
所以 =k·120 +20 , k∈Z.
当k=0时,得角为20 ,
当k=1时,得角为140 ,
当k=2时,得角为260 .
角的概念扩展
1、角的概念
初中是如何定义角的?
从一个点出发引出的两条射线构成的几何图形.
这种概念的优点是形象、直观、容易理解,但它是从图形形状来定义角,因此角的范围是[0 , 360 ),
这种定义称为静态定义,其弊端在于“狭隘”.
生活中很多实例会不在该范围。
体操运动员转体720 ,跳水运动员向内、向外转体1080 ;
经过1小时,时针、分针、秒针各转了多少度?
这些例子不仅不在范围[0 , 360 ) ,而且方向不同,有必要将角的概念推广到任意角,
想想用什么办法才能推广到任意角?
关键是用运动的观点来看待角的变化。
2.角的概念的推广
⑴“旋转”形成角
一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到另一位置OB,就形成角α.
旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB叫做角α的终边,射线的端点O叫做角α的顶点.
⑵.“正角”与“负角”、“0 角”
我们把按逆时针方向旋转所形成的角叫做正角,把按顺时针方向旋转所形成的角叫做负角,如图,以OA为始边的角α=210°,β=-150°,γ=660°,
特别地,当一条射线没有作任何旋转时,我们也认为这时形成了一个角,并把这个角叫做零度角(0 ).
角的记法:角α或可以简记成∠α.
⑶角的概念扩展的意义:
用“旋转”定义角之后,角的范围大大地扩大了
① 角有正负之分; 如: =210 , = 150 , =660 .
② 角可以任意大;
实例:体操动作:旋转2周(360 ×2=720 ) 3周(360 ×3=1080 )
③ 还有零角, 一条射线,没有旋转.
角的概念推广以后,它包括任意大小的正角、负角和零角.
要注意,正角和负角是表示具有相反意义的旋转量,它的正负规定纯属于习惯,就好象与正数、负数的规定一样,零角无正负,就好象数零无正负一样.
用旋转来描述角,需要注意三个要素(旋转中心、旋转方向和旋转量)
(2)旋转方向:旋转变换的方向分为逆时针和顺时针两种,这是一对意义相反的量,根据以往的经验,我们可以把一对意义相反的量用正负数来表示,那么许多问题就可以解决了;
(1)旋转中心:作为角的顶点.
(3)旋转量:
当旋转超过一周时,旋转量即超过360 ,角度的绝对值可大于360 .于是就会出现720 , - 540 等角度.
3.“象限角”
为了研究方便,我们往往在平面直角坐标系中来讨论角。
角的顶点重合于坐标原点,角的始边重合于x轴的正半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角(角的终边落在坐标轴上,则此角不属于任何一个象限)
例如:30 、390 、 330 是第Ⅰ象限角,
300 、 60 是第Ⅳ象限角,
585 、1300 是第Ⅲ象限角,
135 、 2000 是第Ⅱ象限角等
4.终边相同的角
⑴ 观察:390 , 330 角,它们的终边都与30 角的终边相同.
⑵探究:终边相同的角都可以表示成一个0 到360 的角与k(k∈Z)个周角的和:
390 =30 +360 (k=1), 330 =30 360 (k=-1)
30 =30 +0×360 (k=0), 1470 =30 +4×360 (k=4)
1770 =30 5×360 (k=-5)
⑶ 结论:
所有与 终边相同的角连同 在内可以构成一个集合:{β| β=α+k·360 }(k∈Z)
即:任何一个与角 终边相同的角,都可以表示成角 与整数个周角的和
⑷注意以下四点:
① k∈Z;
② 是任意角;
③ k·360 与 之间是“+”号,如k·360 -30 ,应看成k·360 +(-30 );
④ 终边相同的角不一定相等,但相等的角,终边一定相同,终边相同的角有无数多个,它们相差360 的整数倍.
例1. 在0 到360 范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角.
(1) -120 ;(2) 640 ;(3) -950 12′.
解:⑴∵-120 =-360 +240 ,
∴240 的角与-120 的角终边相同,
它是第三象限角.
⑵ ∵640 =360 +280 ,
∴280 的角与640 的角终边相同,
它是第四象限角.
⑶ ∵-950 12’=-3×360 +129 48’,
∴129 48’的角与-950 12’的角终边相同,
它是第二象限角.
例2. 写出与下列各角终边相同的角的集合S,并把S中在-360 ~720 间的角写出来:
(1) 60 ;(2) -21 ;(3) 363 14′.
解:(1) S={β| β=k·360 +60 (k∈Z) },
S中在-360 ~720 间的角是
-1×360 +60 =-280 ;
0×360 +60 =60 ;
1×360 +60 =420 .
(2) S={β| β=k·360 -21 (k∈Z) }
S中在-360 ~720 间的角是
0×360 -21 =-21 ;
1×360 -21 =339 ;
2×360 -21 =699 .
(3) β| β=k·360 + 363 14’ (k∈Z) }
S中在-360 ~720 间的角是
-2×360 +363 14’=-356 46’;
-1×360 +363 14’=3 14’;
0×360 +363 14’=363 14’.
课堂练习
1.锐角是第几象限的角?第一象限的角是否都是锐角?小于90 的角是锐角吗?区间(0 ,90 )内的角是锐角吗?
答:锐角是第一象限角;第一象限角不一定是锐角;小于90 的角可能是零角或负角,故它不一定是锐角;区间(0 ,90 )内的角是锐角.
2.已知角的顶点与坐标系原点重合,始边落在x轴的正半轴上,作出下列各角,并指出它们是哪个象限的角?
(1)420 ,(2) -75 ,(3)855 ,(4) -510 .
答:(1)第一象限角;
(2)第四象限角,
(3)第二象限角,
(4)第三象限角.
3、已知α,β角的终边相同,那么α-β的终边在( )
A x轴的非负半轴上 B y轴的非负半轴上
C x轴的非正半轴上 D y轴的非正半轴上
A
4、终边与坐标轴重合的角的集合是( )
A {β|β=k·360 (k∈Z) }
B {β|β=k·180 (k∈Z) }
C {β|β=k·90 (k∈Z) }
D {β|β=k·180 +90 (k∈Z) }
C
5 、已知角2α的终边在x轴的上方,那么α是( )
A 第一象限角 B 第一、二象限角
C 第一、三象限角 D 第一、四象限角
C
6、若α是第四象限角,则180 -α是( )
A 第一象限角 B 第二象限角
C 第三象限角 D 第四象限角
C
7、在直角坐标系中,若α与β终边互相垂直,那么α与β之间的关系是( )
A. β=α+90o
B β=α±90o
C β=k·360o+90o+α,k∈Z
D β=k·360o±90o+α, k∈Z
D
8、若90 <β<α<135 ,则α-β的范围是__________,α+β的范围是___________;
(0 ,45 )
(180 ,270 )
9、若β的终边与60 角的终边相同,那么在[0 ,360 ]范围内,终边与角 的终边相同的角为______________;
解:β=k·360 +60 ,k∈Z.
所以 =k·120 +20 , k∈Z.
当k=0时,得角为20 ,
当k=1时,得角为140 ,
当k=2时,得角为260 .
