【数学】1.1.2《弧度制》课件(新人教b版必修4)
文档属性
| 名称 | 【数学】1.1.2《弧度制》课件(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
弧度制及换算
在初中几何里,我们学习过角的度量,1度的角是怎样定义的呢?
周角的 为1度的角。
角度制
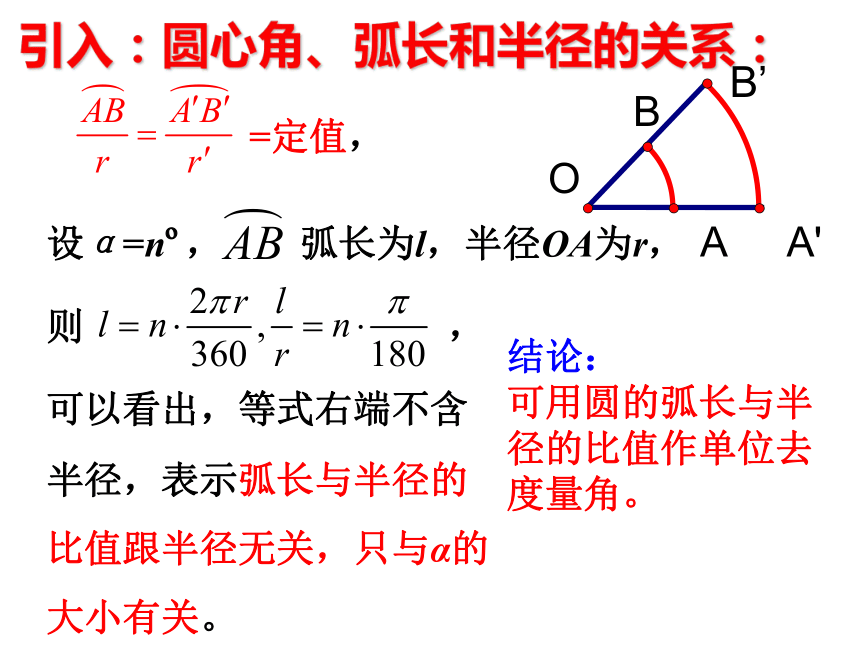
引入:圆心角、弧长和半径的关系:
=定值,
设α=n , 弧长为l,半径OA为r,
则 ,
可以看出,等式右端不含
半径,表示弧长与半径的
比值跟半径无关,只与α的
大小有关。
结论:
可用圆的弧长与半径的比值作单位去度量角。
B
A'
O
A
B’
定义:
长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度记作rad。这种以弧度为单位来度量角的制度叫做弧度制。
注:单位rad可以略去不写。
弧度制与角度制相比:
(1) 弧度制是以“弧度”为单位的度量角的单位制,角度制是以“度”为单位来度量角的单位制
(2)1弧度是弧长等于半径长的圆弧所对的圆心角的大小,而1度是圆周 的所对的圆心角的大小; 1弧度≠1
(3)以弧度和度为单位的角,都是一个与半径无关的定值。
弧度制与角度制的换算
① 零角既是0 角,又是0 rad角
② 平角、周角的弧度数:
180°= rad 360°=2 rad
③角 的弧度数的绝对值:
1 =
1 rad
用弧度制表示弧长公式:
弧长等于弧所对的圆心角弧度的绝对值与半径的积.
① 弧长公式:
由公式:
比公式 简单.
② 扇形面积公式
其中l是扇形弧长,R是圆的半径。
证明:设扇形所对的圆心角为n (αrad),则
又 αR=l,所以
用弧度制表示扇形面积公式:
例1. 把112 30′化成弧度(用π表示)。
112 30′=112.5× = .
例2. 把 化成度。
例3. 填写下表:
角度 0° 30° 45° 60° 90° 120°
弧度
角度 135° 150° 180° 210° 225° 240°
弧度
角度 270° 300° 315° 330° 360°
弧度
0
π
2π
例4. 扇形AOB中, 所对的圆心角是60 ,半径是50米,求 的长l
解:因为60 = ,所以
l=α·r= ×50≈52.5 .
答: 的长约为52.5米.
例5. 在半径为R的圆中,240 的中心角所对的弧长为 ,面积为2R2的扇形的中心角等于 弧度。
解:(1)240 = ,根据l=αR,得
(2)根据S= lR= αR2,且S=2R2.
所以 α=4.
例6.与角-1825 的终边相同,且绝对值最小的角的度数是___,合___弧度。
解:-1825 =-5×360 -25 ,
所以与角-1825 的终边相同,且绝对值最小的角是-25 .
合
例7. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?扇形的面积是多少?
解:周长=2πR=2R+l,所以l=2(π-1)R.
所以扇形的中心角是2(π-1) rad.
扇形面积是
弧度制及换算
在初中几何里,我们学习过角的度量,1度的角是怎样定义的呢?
周角的 为1度的角。
角度制
引入:圆心角、弧长和半径的关系:
=定值,
设α=n , 弧长为l,半径OA为r,
则 ,
可以看出,等式右端不含
半径,表示弧长与半径的
比值跟半径无关,只与α的
大小有关。
结论:
可用圆的弧长与半径的比值作单位去度量角。
B
A'
O
A
B’
定义:
长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度记作rad。这种以弧度为单位来度量角的制度叫做弧度制。
注:单位rad可以略去不写。
弧度制与角度制相比:
(1) 弧度制是以“弧度”为单位的度量角的单位制,角度制是以“度”为单位来度量角的单位制
(2)1弧度是弧长等于半径长的圆弧所对的圆心角的大小,而1度是圆周 的所对的圆心角的大小; 1弧度≠1
(3)以弧度和度为单位的角,都是一个与半径无关的定值。
弧度制与角度制的换算
① 零角既是0 角,又是0 rad角
② 平角、周角的弧度数:
180°= rad 360°=2 rad
③角 的弧度数的绝对值:
1 =
1 rad
用弧度制表示弧长公式:
弧长等于弧所对的圆心角弧度的绝对值与半径的积.
① 弧长公式:
由公式:
比公式 简单.
② 扇形面积公式
其中l是扇形弧长,R是圆的半径。
证明:设扇形所对的圆心角为n (αrad),则
又 αR=l,所以
用弧度制表示扇形面积公式:
例1. 把112 30′化成弧度(用π表示)。
112 30′=112.5× = .
例2. 把 化成度。
例3. 填写下表:
角度 0° 30° 45° 60° 90° 120°
弧度
角度 135° 150° 180° 210° 225° 240°
弧度
角度 270° 300° 315° 330° 360°
弧度
0
π
2π
例4. 扇形AOB中, 所对的圆心角是60 ,半径是50米,求 的长l
解:因为60 = ,所以
l=α·r= ×50≈52.5 .
答: 的长约为52.5米.
例5. 在半径为R的圆中,240 的中心角所对的弧长为 ,面积为2R2的扇形的中心角等于 弧度。
解:(1)240 = ,根据l=αR,得
(2)根据S= lR= αR2,且S=2R2.
所以 α=4.
例6.与角-1825 的终边相同,且绝对值最小的角的度数是___,合___弧度。
解:-1825 =-5×360 -25 ,
所以与角-1825 的终边相同,且绝对值最小的角是-25 .
合
例7. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?扇形的面积是多少?
解:周长=2πR=2R+l,所以l=2(π-1)R.
所以扇形的中心角是2(π-1) rad.
扇形面积是
