【数学】1.2.1《任意角的三角函数(1)》课件(新人教b版必修4)
文档属性
| 名称 | 【数学】1.2.1《任意角的三角函数(1)》课件(新人教b版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 86.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 16:11:36 | ||
图片预览


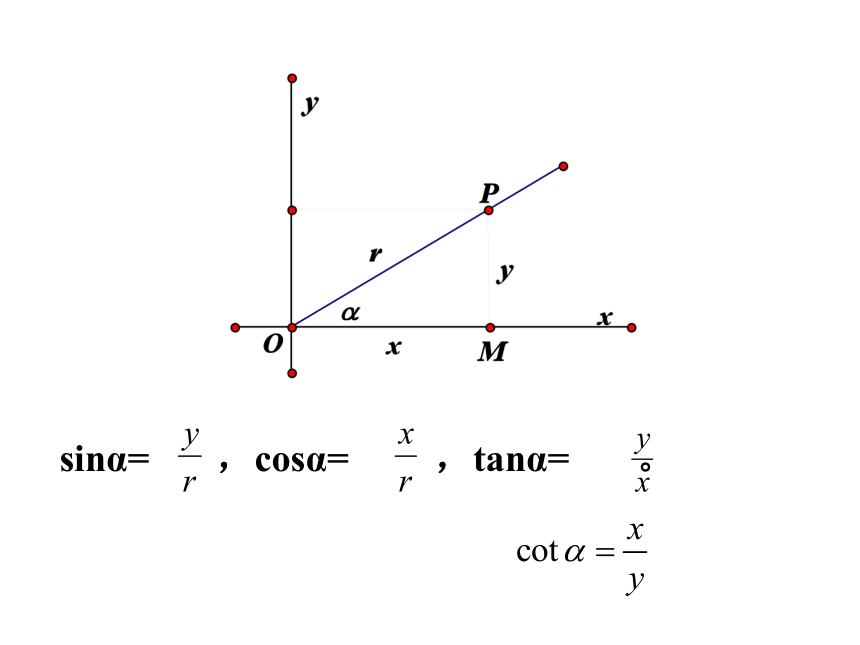





文档简介
(共22张PPT)
1.2.1 三角函数的定义(一)
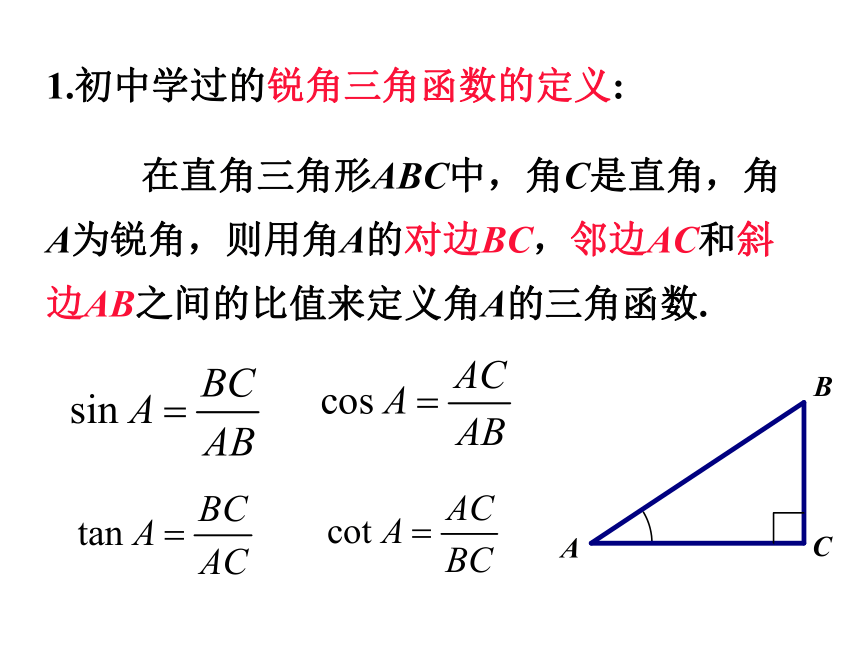
1.初中学过的锐角三角函数的定义:
在直角三角形ABC中,角C是直角,角A为锐角,则用角A的对边BC,邻边AC和斜边AB之间的比值来定义角A的三角函数.
2.用坐标的形式表示出初中所学的锐角三角函数:
以坐标原点为角α的顶点,以OX轴的正方向为角α的始边,则角α的终边落在直角坐标系的第一象限内,若点P (x,y)是角α终边上的任意一点,点P到原点O的距离是r ,试将角α的三角函数用x、y、r的式子表示出来
sinα= ,cosα= ,tanα= 。
3. 任意角的三角函数 :
(1)确立任意角α在直角坐标系中的位置;
以坐标原点为角α的顶点,以OX轴的正方向为角α的始边;
(2)在其终边上取点A,使OA=1,点A的坐标为(l, m),再任取一点P(x,y),设点P到原点的距离为r,OP =r(r≠0),根据三角形的相似知识得:
因为A、P在同一象限内,所以它们的坐标符号相同,因此得
不论点P在终边上的位置如何,它们都是定值,它们只依赖于α的大小,与点P在α终边上的位置无关。即当点P在α的终边上的位置变化时,这三个比值始终等于定值。
叫做角α的余弦,记作cosα ,
即cosα= ;
叫做角α的正弦,记作sinα,
即sinα= ;
叫做角α的正切,记作tanα,
即 tanα=
依照上述定义,对于每一个确定的角α,都分别有唯一确定的余弦值、正弦值与之对应: 当α≠2kπ± (k∈Z)时,它有唯一的正切值与之对应. 因此这三个对应法则都是以α为自变量的函数,分别叫做角α的余弦函数、正弦函数和正切函数。
3.角α的其他三种函数:
角α的正割:
角α的余割:
角α的余切:
4. 几点说明:
(1) 这里提到的角α是“任意角”,当β=2kπ+α(k∈Z)时,β与α的同名三角函数值应该是相等的,即凡是终边相同的角的三角函数值都相等。
(2) 定义中只说怎样的比值叫做α的什么函数,并没有说α的终边在什么位置(终边在坐标轴上除外),即函数的定义与α的终边位置无关。
实际上,如果终边在坐标轴上,上述定义同样适用。
(3) 三角函数是以“比值”为函数值的函数。
(4) 对于正弦函数sinα= , 因为r>0,所以恒有意义,即α取任意实数, 恒有意义,也就是说sinα恒有意义,所以正弦函数的定义域是R;类似地可写出余弦函数的定义域是R;
对于正切函数tanα= , 因为x=0时, 无意义,又当且仅当α的终边落在y轴上时,才有x=0,所以当α的终边落不在y轴上时,
恒有意义,即tanα= 恒有意义,所以正切函数的定义域是{α|α≠kπ+ (k∈Z)}
从而三角函数的定义域是
y=sinα, α∈R
y=cosα, α∈R
y=tanα ,α≠kπ+ (k∈Z)
例1.已知角α的终边过点P(2,-3),求α的六个三角函数值。
解:因为x=2,y=-3,所以
sinα=
cosα=
tanα=
cotα=
secα=
cscα=
解:(1)因为当α=0时,x=r,y=0 .所以
例2. 求下列各角六个三角函数值:
(1)0;(2)π;(3)
sin0=0,cos0=1,tan0=0,
csc0不存在,sec0=1,cot0不存在.
(2) π;
解:(2)因为当α=π时,x=-r,y=0 .所以
sinπ=0,cosπ=-1,tanπ=0,
Cscπ不存在,secπ=-1,cotπ不存在.
(3)
解:(3)因为当α= 时,x=0,y=-r .所以
sin =-1,cos =0,tan 不存在,
csc =-1,sec 不存在,cot =0.
例3. 角α的终边过点P(-b,4),且cosα=
则b的值是( )
解:r=
cosα=
解得b=3.
(A)3 (B)-3 (C)±3 (D)5
A
例4. 在直角坐标系中,终边过点(1, )的所有角的集合是 .
解:点(1, )在第一象限,且x=1,y=
所以r=2,sinα= ,cosα=
所以满足条件的角α=2kπ+
{α|α=2kπ+ ,k∈Z}
例5. 已知角α的终边上一点P(- ,y)(其中y≠0),且sinα= ,求cosα和tanα.
解:sinα=
解得y2=5,y=
当y= 时,cosα= ,tanα=
当y=- 时,cosα= ,tanα=
1.2.1 三角函数的定义(一)
1.初中学过的锐角三角函数的定义:
在直角三角形ABC中,角C是直角,角A为锐角,则用角A的对边BC,邻边AC和斜边AB之间的比值来定义角A的三角函数.
2.用坐标的形式表示出初中所学的锐角三角函数:
以坐标原点为角α的顶点,以OX轴的正方向为角α的始边,则角α的终边落在直角坐标系的第一象限内,若点P (x,y)是角α终边上的任意一点,点P到原点O的距离是r ,试将角α的三角函数用x、y、r的式子表示出来
sinα= ,cosα= ,tanα= 。
3. 任意角的三角函数 :
(1)确立任意角α在直角坐标系中的位置;
以坐标原点为角α的顶点,以OX轴的正方向为角α的始边;
(2)在其终边上取点A,使OA=1,点A的坐标为(l, m),再任取一点P(x,y),设点P到原点的距离为r,OP =r(r≠0),根据三角形的相似知识得:
因为A、P在同一象限内,所以它们的坐标符号相同,因此得
不论点P在终边上的位置如何,它们都是定值,它们只依赖于α的大小,与点P在α终边上的位置无关。即当点P在α的终边上的位置变化时,这三个比值始终等于定值。
叫做角α的余弦,记作cosα ,
即cosα= ;
叫做角α的正弦,记作sinα,
即sinα= ;
叫做角α的正切,记作tanα,
即 tanα=
依照上述定义,对于每一个确定的角α,都分别有唯一确定的余弦值、正弦值与之对应: 当α≠2kπ± (k∈Z)时,它有唯一的正切值与之对应. 因此这三个对应法则都是以α为自变量的函数,分别叫做角α的余弦函数、正弦函数和正切函数。
3.角α的其他三种函数:
角α的正割:
角α的余割:
角α的余切:
4. 几点说明:
(1) 这里提到的角α是“任意角”,当β=2kπ+α(k∈Z)时,β与α的同名三角函数值应该是相等的,即凡是终边相同的角的三角函数值都相等。
(2) 定义中只说怎样的比值叫做α的什么函数,并没有说α的终边在什么位置(终边在坐标轴上除外),即函数的定义与α的终边位置无关。
实际上,如果终边在坐标轴上,上述定义同样适用。
(3) 三角函数是以“比值”为函数值的函数。
(4) 对于正弦函数sinα= , 因为r>0,所以恒有意义,即α取任意实数, 恒有意义,也就是说sinα恒有意义,所以正弦函数的定义域是R;类似地可写出余弦函数的定义域是R;
对于正切函数tanα= , 因为x=0时, 无意义,又当且仅当α的终边落在y轴上时,才有x=0,所以当α的终边落不在y轴上时,
恒有意义,即tanα= 恒有意义,所以正切函数的定义域是{α|α≠kπ+ (k∈Z)}
从而三角函数的定义域是
y=sinα, α∈R
y=cosα, α∈R
y=tanα ,α≠kπ+ (k∈Z)
例1.已知角α的终边过点P(2,-3),求α的六个三角函数值。
解:因为x=2,y=-3,所以
sinα=
cosα=
tanα=
cotα=
secα=
cscα=
解:(1)因为当α=0时,x=r,y=0 .所以
例2. 求下列各角六个三角函数值:
(1)0;(2)π;(3)
sin0=0,cos0=1,tan0=0,
csc0不存在,sec0=1,cot0不存在.
(2) π;
解:(2)因为当α=π时,x=-r,y=0 .所以
sinπ=0,cosπ=-1,tanπ=0,
Cscπ不存在,secπ=-1,cotπ不存在.
(3)
解:(3)因为当α= 时,x=0,y=-r .所以
sin =-1,cos =0,tan 不存在,
csc =-1,sec 不存在,cot =0.
例3. 角α的终边过点P(-b,4),且cosα=
则b的值是( )
解:r=
cosα=
解得b=3.
(A)3 (B)-3 (C)±3 (D)5
A
例4. 在直角坐标系中,终边过点(1, )的所有角的集合是 .
解:点(1, )在第一象限,且x=1,y=
所以r=2,sinα= ,cosα=
所以满足条件的角α=2kπ+
{α|α=2kπ+ ,k∈Z}
例5. 已知角α的终边上一点P(- ,y)(其中y≠0),且sinα= ,求cosα和tanα.
解:sinα=
解得y2=5,y=
当y= 时,cosα= ,tanα=
当y=- 时,cosα= ,tanα=
