【数学】1.2.1《任意角的三角函数(2)》课件(新人教b版必修4)
文档属性
| 名称 | 【数学】1.2.1《任意角的三角函数(2)》课件(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 51.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
1.2.1三角函数的定义(二)
1. 三角函数的定义:
设α是一个任意角,在α的终边上任取(异于原点的)一点P(x, y),则P与原点的距离为
,比值 只与角α的大小有关.
以上六种函数,统称为三角函数.
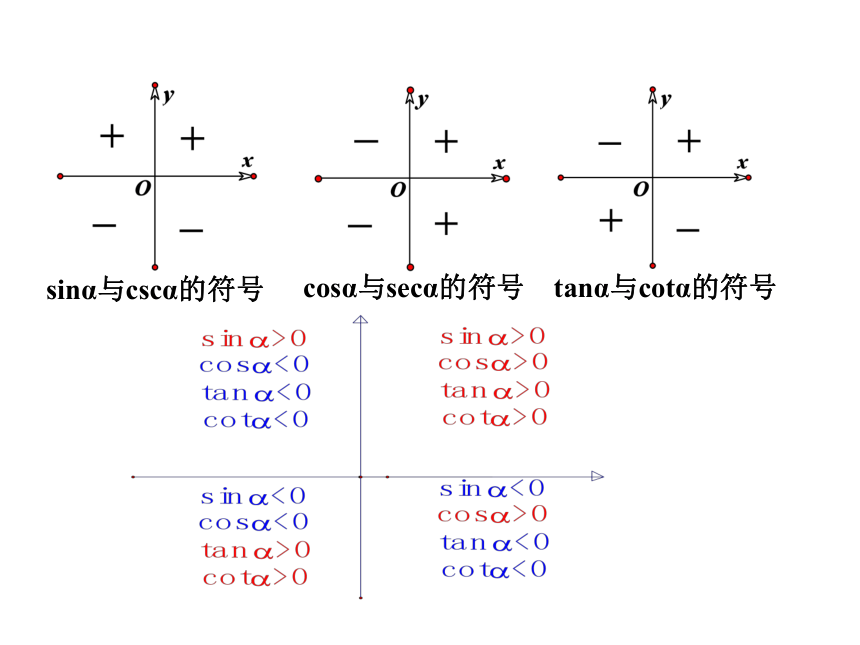
2. 三角函数在各象限内的符号
角α是“任意角”, 由三角函数定义可知,由于P(x, y)点的坐标x, y的正负是随角α所在的象限的变化而不同,所以三角函数的符号应由角α所在的象限确定.
当角α在第一象限时,由于x>0,y>0,所以
sinα>0,cosα>0,tanα>0,cotα>0,secα>0,cscα>0.
当角α在第二象限时,由于x<0,y>0,所以
sinα>0,cosα<0,tanα<0,cotα<0,secα<0,cscα>0.
当角α在第三象限时,由于x<0,y<0,所以
sinα<0,cosα<0,tanα>0,cotα>0,secα<0,cscα<0.
当角α在第四象限时,由于x>0,y<0,所以
sinα<0,cosα>0,tanα<0,cotα<0,secα>0,cscα<0.
cosα与secα的符号
sinα与cscα的符号
tanα与cotα的符号
例1. 确定下列三角函数值的符号:?
(1)cos250 ; (2)
(3)tan(-672 );(4)
解: (1)250 在第三象限,所以cos250 <0.
(2) - 在第四象限,所以sin(- )<0.
(3) -672 在第一象限,所以tan(-672 )>0.
(4) 在第四象限,所以tan( )<0.
例2.设sinθ<0且tanθ>0,确定θ是第几象限的角。
解:因为sinθ<0,所以θ可能是第三、四象限的角,又tanθ>0,θ可能是第一、三象限的角,综上所述,θ是第三象限的角。
例3.若三角形的两内角 , 满足sin cos <0,则此三角形必为( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 以上三种情况都可能
B
例4.若α是第三象限角,则下列各式中不成立的是( )
A. sin +cos <0 B. tan sin <0
C. cos cot <0 D. cot csc <0
B
例5.已知 ,则 为第几象限角?
解:因为 ,所以sin2 >0,
则2kπ<2 <2kπ+π, kπ<所以 是第一或第三象限角.
练习
1.函数y= + + 的值域是 ( )
(A) {-1,1} (B) {-1,1,3}
(C) {-1,3} (D) {1,3}
C
2.已知角θ的终边上有一点P(-4a, 3a)(a≠0),则2sinθ+cosθ的值是 ( )
(A) (B) -
(C) 或 - (D) 不确定
C
3. 设A是第三象限角,且|sin |= -sin ,则是 ( )
(A)第一象限角 (B) 第二象限角
(C)第三象限角 (D) 第四象限角
D
4. sin2·cos3·tan4的值 ( )
(A)大于0 (B)小于0
(C)等于0 (D)不确定
B
5.若sinθ·cosθ>0, 则θ是第 象限的角
一、三
0
6. sin(- π)+cos π·tan4π -cos π= .
解:∵P(-2, y)是角θ终边上一点, r=
7.已知P(-2,y)是角θ终边上一点,且sinθ= - ,求cosθ的值.
解得y=-1.
所以cosθ= - .
1.2.1三角函数的定义(二)
1. 三角函数的定义:
设α是一个任意角,在α的终边上任取(异于原点的)一点P(x, y),则P与原点的距离为
,比值 只与角α的大小有关.
以上六种函数,统称为三角函数.
2. 三角函数在各象限内的符号
角α是“任意角”, 由三角函数定义可知,由于P(x, y)点的坐标x, y的正负是随角α所在的象限的变化而不同,所以三角函数的符号应由角α所在的象限确定.
当角α在第一象限时,由于x>0,y>0,所以
sinα>0,cosα>0,tanα>0,cotα>0,secα>0,cscα>0.
当角α在第二象限时,由于x<0,y>0,所以
sinα>0,cosα<0,tanα<0,cotα<0,secα<0,cscα>0.
当角α在第三象限时,由于x<0,y<0,所以
sinα<0,cosα<0,tanα>0,cotα>0,secα<0,cscα<0.
当角α在第四象限时,由于x>0,y<0,所以
sinα<0,cosα>0,tanα<0,cotα<0,secα>0,cscα<0.
cosα与secα的符号
sinα与cscα的符号
tanα与cotα的符号
例1. 确定下列三角函数值的符号:?
(1)cos250 ; (2)
(3)tan(-672 );(4)
解: (1)250 在第三象限,所以cos250 <0.
(2) - 在第四象限,所以sin(- )<0.
(3) -672 在第一象限,所以tan(-672 )>0.
(4) 在第四象限,所以tan( )<0.
例2.设sinθ<0且tanθ>0,确定θ是第几象限的角。
解:因为sinθ<0,所以θ可能是第三、四象限的角,又tanθ>0,θ可能是第一、三象限的角,综上所述,θ是第三象限的角。
例3.若三角形的两内角 , 满足sin cos <0,则此三角形必为( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 以上三种情况都可能
B
例4.若α是第三象限角,则下列各式中不成立的是( )
A. sin +cos <0 B. tan sin <0
C. cos cot <0 D. cot csc <0
B
例5.已知 ,则 为第几象限角?
解:因为 ,所以sin2 >0,
则2kπ<2 <2kπ+π, kπ<
练习
1.函数y= + + 的值域是 ( )
(A) {-1,1} (B) {-1,1,3}
(C) {-1,3} (D) {1,3}
C
2.已知角θ的终边上有一点P(-4a, 3a)(a≠0),则2sinθ+cosθ的值是 ( )
(A) (B) -
(C) 或 - (D) 不确定
C
3. 设A是第三象限角,且|sin |= -sin ,则是 ( )
(A)第一象限角 (B) 第二象限角
(C)第三象限角 (D) 第四象限角
D
4. sin2·cos3·tan4的值 ( )
(A)大于0 (B)小于0
(C)等于0 (D)不确定
B
5.若sinθ·cosθ>0, 则θ是第 象限的角
一、三
0
6. sin(- π)+cos π·tan4π -cos π= .
解:∵P(-2, y)是角θ终边上一点, r=
7.已知P(-2,y)是角θ终边上一点,且sinθ= - ,求cosθ的值.
解得y=-1.
所以cosθ= - .
