【数学】1.2.2《单位圆与三角函数线》课件(1)(新人教b版必修4)
文档属性
| 名称 | 【数学】1.2.2《单位圆与三角函数线》课件(1)(新人教b版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 102.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 16:11:36 | ||
图片预览




文档简介
(共21张PPT)
单位圆与三角函数线
由三角函数的定义我们知道,对于角α的各种三角函数我们都是用比值来表示的,或者说是用数来表示的,今天我们再来学习正弦、余弦、正切函数的另一种表示方法——几何表示法
单位圆的概念
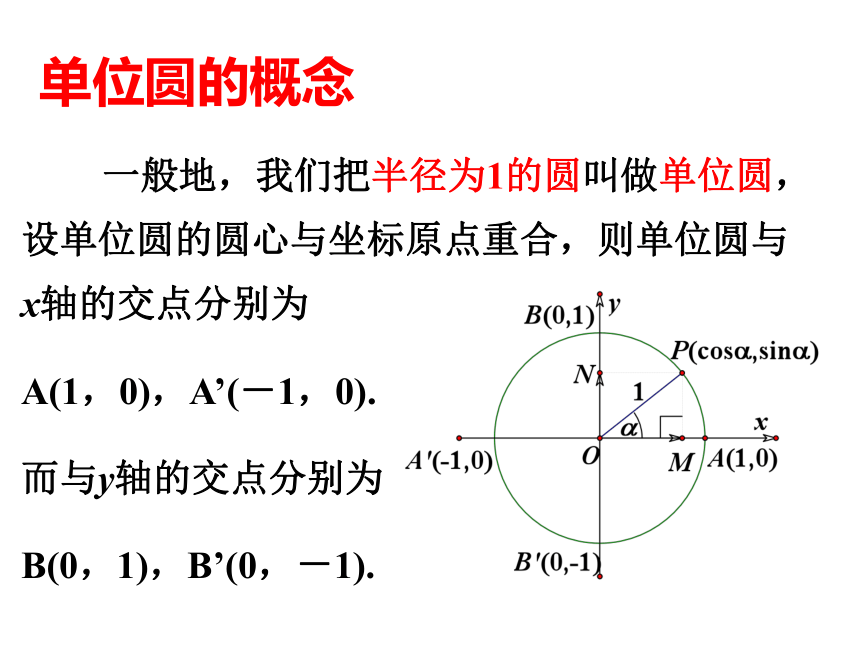
一般地,我们把半径为1的圆叫做单位圆,设单位圆的圆心与坐标原点重合,则单位圆与x轴的交点分别为
A(1,0),A’(-1,0).
而与y轴的交点分别为
B(0,1),B’(0,-1).
有向线段的概念:
带有方向的线段叫有向线段 ;
有向线段的数值由其长度大小和方向来决定。
如在数轴上,|OA|=3,|OB|=3
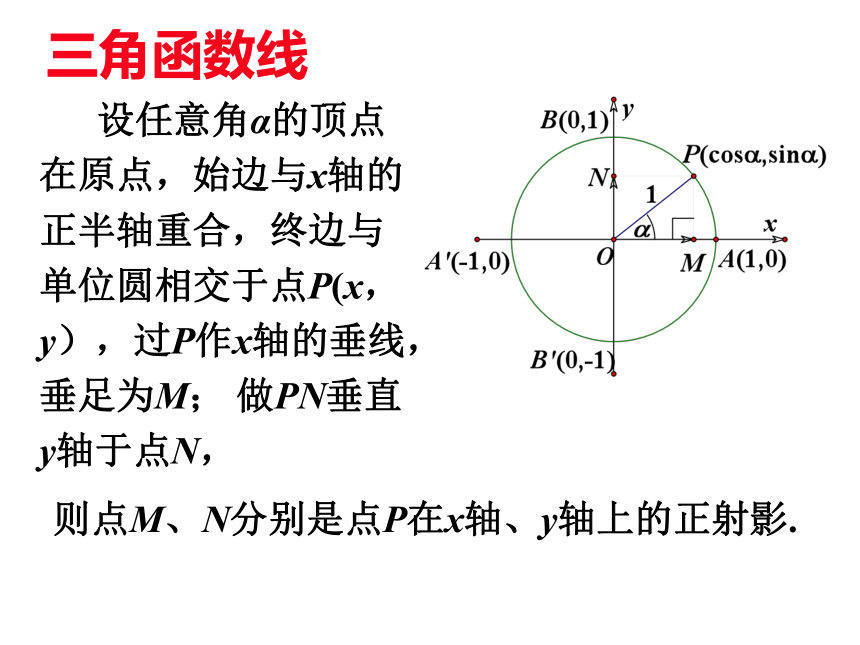
设任意角α的顶点在原点,始边与x轴的正半轴重合,终边与单位圆相交于点P(x,y),过P作x轴的垂线,垂足为M; 做PN垂直y轴于点N,
则点M、N分别是点P在x轴、y轴上的正射影.
三角函数线
根据三角函数的定义有点P的坐标为(cosα,sinα)
其中cosα=OM,sinα=ON.
这就是说,角α的余弦和正弦分别等于角α的终边与单位圆交点的横坐标与纵坐标.
以A为原点建立y’轴与y轴同向,y’轴与α角的终边(或其反向延长线)相交于点T(或T ’),则tanα=AT(或AT ’)
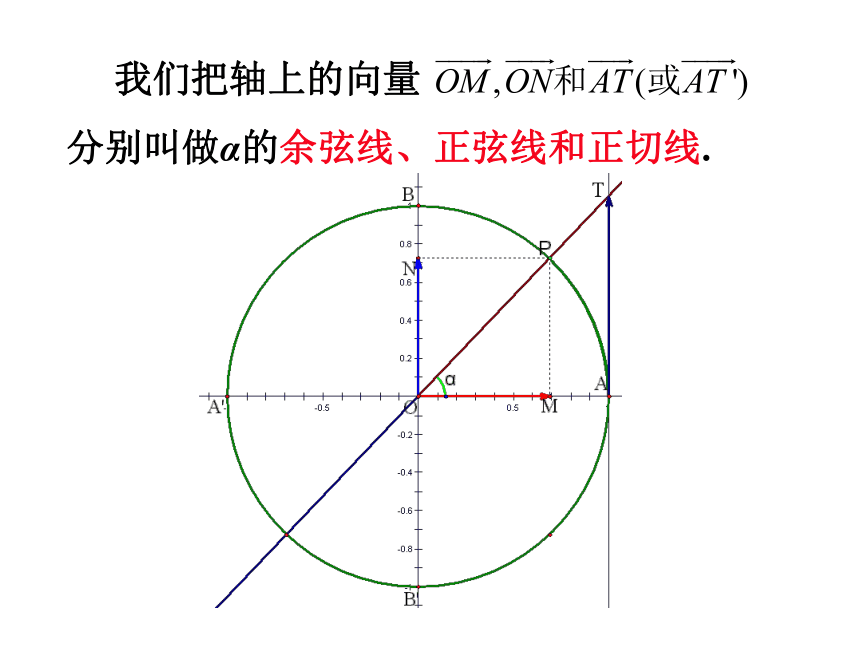
我们把轴上的向量
分别叫做α的余弦线、正弦线和正切线.
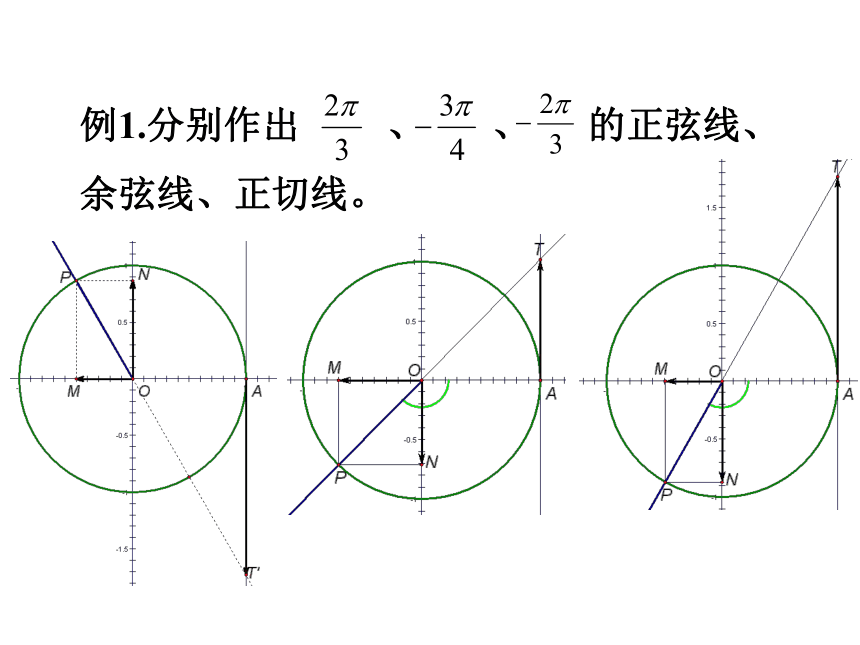
例1.分别作出 、 、 的正弦线、余弦线、正切线。
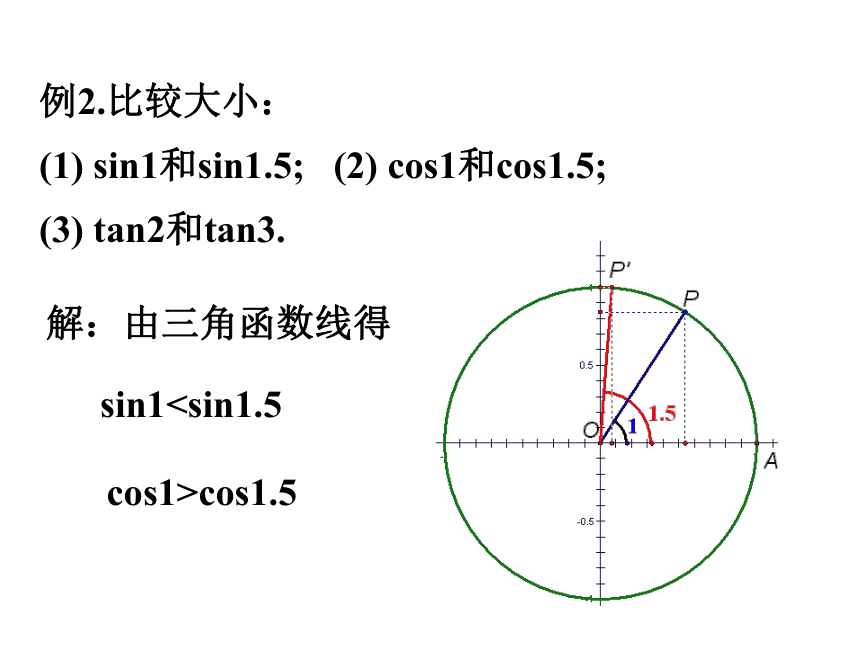
例2.比较大小:
(1) sin1和sin1.5; (2) cos1和cos1.5;
(3) tan2和tan3.
解:由三角函数线得
sin1cos1>cos1.5
tan2例3. 已知sinx=0.5,求角x的大小.(0 解:由在y轴上找到y=0.5的点,做x轴的平行线,交单位圆于点P和P’两点,由三角函数线知
x1=30 , x2=150 .
例4. 利用三角函数线证明|sinα|+|cosα|≥1.
证明:在△OMP中,OP=1,OM=|cosα|, MP=ON=|sinα|,
因为三角形两边之和大于第三边,所以
|sinα|+|cosα|≥1。
例5. 已知α∈(0, ),试证明sinα<α证明:sinα=|ON|=|MP|,
α =
tanα=|AT|.
又
所以
即sinα<α小结:
1. 给定任意一个角α,都能在单位圆中作出它的正弦线、余弦线、正切线。
2. 三角函数线的位置 :
正弦线为从原点到α的终边与单位圆的交点在y轴上的射影的有向线段;
余弦线为从原点到α的终边与单位圆的交点在x轴上的射影的有向线段;
正切线在过单位圆与x轴正方向的交点的切线上,为有向线段
3. 特殊情况:
① 当角的终边在x轴上时,点P与点M重合,点T与点A重合,这时正弦线与正切线都变成了一点,数量为零,而余弦线OM=1或-1。
② 当角的终边在y轴上时,正弦线MP=1或-1余弦线变成了一点,它表示的数量为零,正切线不存在。
练习
1.函数y= + + 的值域是 ( )
(A) {-1,1} (B) {-1,1,3}
(C) {-1,3} (D) {1,3}
C
2.已知角θ的终边上有一点P(-4a, 3a)(a≠0),则2sinθ+cosθ的值是 ( )
(A) (B) -
(C) 或 - (D) 不确定
C
3. 设A是第三象限角,且|sin |= -sin ,则是 ( )
(A)第一象限角 (B) 第二象限角
(C)第三象限角 (D) 第四象限角
D
4. sin2·cos3·tan4的值 ( )
(A)大于0 (B)小于0
(C)等于0 (D)不确定
B
5.若sinθ·cosθ>0, 则θ是第 象限的角
一、三
0
6. sin(- π)+cos π·tan4π -cos π= .
解:∵P(-2, y)是角θ终边上一点, r=
7.已知P(-2,y)是角θ终边上一点,且sinθ= - ,求cosθ的值.
解得y=-1.
所以cosθ= - .
单位圆与三角函数线
由三角函数的定义我们知道,对于角α的各种三角函数我们都是用比值来表示的,或者说是用数来表示的,今天我们再来学习正弦、余弦、正切函数的另一种表示方法——几何表示法
单位圆的概念
一般地,我们把半径为1的圆叫做单位圆,设单位圆的圆心与坐标原点重合,则单位圆与x轴的交点分别为
A(1,0),A’(-1,0).
而与y轴的交点分别为
B(0,1),B’(0,-1).
有向线段的概念:
带有方向的线段叫有向线段 ;
有向线段的数值由其长度大小和方向来决定。
如在数轴上,|OA|=3,|OB|=3
设任意角α的顶点在原点,始边与x轴的正半轴重合,终边与单位圆相交于点P(x,y),过P作x轴的垂线,垂足为M; 做PN垂直y轴于点N,
则点M、N分别是点P在x轴、y轴上的正射影.
三角函数线
根据三角函数的定义有点P的坐标为(cosα,sinα)
其中cosα=OM,sinα=ON.
这就是说,角α的余弦和正弦分别等于角α的终边与单位圆交点的横坐标与纵坐标.
以A为原点建立y’轴与y轴同向,y’轴与α角的终边(或其反向延长线)相交于点T(或T ’),则tanα=AT(或AT ’)
我们把轴上的向量
分别叫做α的余弦线、正弦线和正切线.
例1.分别作出 、 、 的正弦线、余弦线、正切线。
例2.比较大小:
(1) sin1和sin1.5; (2) cos1和cos1.5;
(3) tan2和tan3.
解:由三角函数线得
sin1
tan2
x1=30 , x2=150 .
例4. 利用三角函数线证明|sinα|+|cosα|≥1.
证明:在△OMP中,OP=1,OM=|cosα|, MP=ON=|sinα|,
因为三角形两边之和大于第三边,所以
|sinα|+|cosα|≥1。
例5. 已知α∈(0, ),试证明sinα<α
α =
tanα=|AT|.
又
所以
即sinα<α
1. 给定任意一个角α,都能在单位圆中作出它的正弦线、余弦线、正切线。
2. 三角函数线的位置 :
正弦线为从原点到α的终边与单位圆的交点在y轴上的射影的有向线段;
余弦线为从原点到α的终边与单位圆的交点在x轴上的射影的有向线段;
正切线在过单位圆与x轴正方向的交点的切线上,为有向线段
3. 特殊情况:
① 当角的终边在x轴上时,点P与点M重合,点T与点A重合,这时正弦线与正切线都变成了一点,数量为零,而余弦线OM=1或-1。
② 当角的终边在y轴上时,正弦线MP=1或-1余弦线变成了一点,它表示的数量为零,正切线不存在。
练习
1.函数y= + + 的值域是 ( )
(A) {-1,1} (B) {-1,1,3}
(C) {-1,3} (D) {1,3}
C
2.已知角θ的终边上有一点P(-4a, 3a)(a≠0),则2sinθ+cosθ的值是 ( )
(A) (B) -
(C) 或 - (D) 不确定
C
3. 设A是第三象限角,且|sin |= -sin ,则是 ( )
(A)第一象限角 (B) 第二象限角
(C)第三象限角 (D) 第四象限角
D
4. sin2·cos3·tan4的值 ( )
(A)大于0 (B)小于0
(C)等于0 (D)不确定
B
5.若sinθ·cosθ>0, 则θ是第 象限的角
一、三
0
6. sin(- π)+cos π·tan4π -cos π= .
解:∵P(-2, y)是角θ终边上一点, r=
7.已知P(-2,y)是角θ终边上一点,且sinθ= - ,求cosθ的值.
解得y=-1.
所以cosθ= - .
