【数学】1.2.3《同角三角函数的基本关系式》课件(1)(新人教b版必修4)
文档属性
| 名称 | 【数学】1.2.3《同角三角函数的基本关系式》课件(1)(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 87.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
同角三角函数关系式
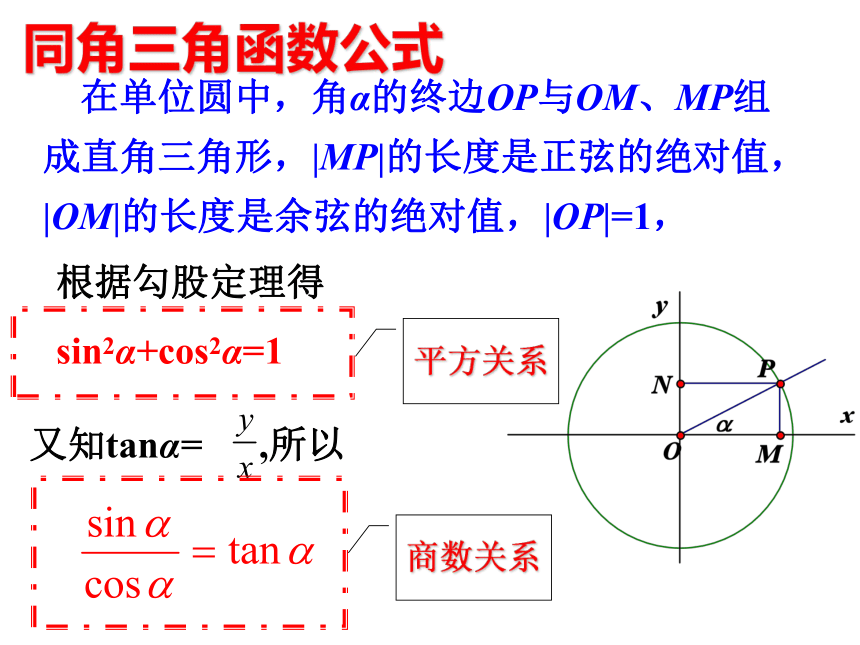
在单位圆中,角α的终边OP与OM、MP组成直角三角形,|MP|的长度是正弦的绝对值,|OM|的长度是余弦的绝对值,|OP|=1,
根据勾股定理得
sin2α+cos2α=1
又知tanα= ,所以
平方关系
商数关系
同角三角函数公式
注意:
1. 公式中的角一定是同角,否则公式可能不成立. 如sin230 +cos260 ≠1.
2.同角不要拘泥于形式α, ,6α等等都可以.
如sin24α+cos24α=1.
3. 商数关系中注意限制条件. 即cosα≠0. α≠kπ+ ,k∈Z.
(1)给定角的一个三角函数值,求这个角的其余三角函数值。
应用:
(2) 化简三角函数式和证明三角恒等式。
应用的方法:
正用, 逆用、变形用.
例1 已知 ,并且α是第二象限角,求α的余弦和正切值.
解:∵sin2α+cos2α=1,α是第二象限角.
例2.已知 ,求sinα、tanα的值.
解: ∵cosα<0 ∴α是第二或第三象限角.
(ⅰ)当α是第二象限角时,
(ⅱ)当α是第三象限角时,
例3. 已知sinα-cosα= ,180 <α<270 .
求tanα的值。
解:以题意和基本三角恒等式,得到方程组
消去sinα,得5cos2α- cosα-2=0,
由方程解得cosα=
或cosα=
因为180 <α<270 ,所以cosα<0,即
cosα=
代入原方程组得sinα=
于是tanα= =2.
例4化简:
解:原式=
例5 化简:
解:原式=
=cosθ.
化简方向:
切化弦
例6 已知tanθ=2求值:
解:(1)分子分母同除以cosθ
原式=
=1/7.
化简方向:
弦化切
(2)分子“1”换为 “sin2θ +cos2θ”
原式=
=5/3.
例7. 求证:(1)sin4α-cos4α=2sin2α-1;
证明:左边=(sin2α+cos2α)(sin2α-cos2α)
=sin2α-cos2α
=sin2α-(1-sin2α)
=2sin2α-1右边.
所以原等式成立.
(2)
证明:
原式右边=tan2α(1-cos2α)
=tan2α-tan2αcos2α
=tan2α-sin2α
=左边.
(3)
证明:左边
=右边
∴原等式成立.
证明等式的常用方法:
1.从等式的一边证得它等于另一边;
2.先证明另外一个等式成立,从而推出需要
证明的等式成立;
3.利用作差(作商)的方法。
同角三角函数关系式
在单位圆中,角α的终边OP与OM、MP组成直角三角形,|MP|的长度是正弦的绝对值,|OM|的长度是余弦的绝对值,|OP|=1,
根据勾股定理得
sin2α+cos2α=1
又知tanα= ,所以
平方关系
商数关系
同角三角函数公式
注意:
1. 公式中的角一定是同角,否则公式可能不成立. 如sin230 +cos260 ≠1.
2.同角不要拘泥于形式α, ,6α等等都可以.
如sin24α+cos24α=1.
3. 商数关系中注意限制条件. 即cosα≠0. α≠kπ+ ,k∈Z.
(1)给定角的一个三角函数值,求这个角的其余三角函数值。
应用:
(2) 化简三角函数式和证明三角恒等式。
应用的方法:
正用, 逆用、变形用.
例1 已知 ,并且α是第二象限角,求α的余弦和正切值.
解:∵sin2α+cos2α=1,α是第二象限角.
例2.已知 ,求sinα、tanα的值.
解: ∵cosα<0 ∴α是第二或第三象限角.
(ⅰ)当α是第二象限角时,
(ⅱ)当α是第三象限角时,
例3. 已知sinα-cosα= ,180 <α<270 .
求tanα的值。
解:以题意和基本三角恒等式,得到方程组
消去sinα,得5cos2α- cosα-2=0,
由方程解得cosα=
或cosα=
因为180 <α<270 ,所以cosα<0,即
cosα=
代入原方程组得sinα=
于是tanα= =2.
例4化简:
解:原式=
例5 化简:
解:原式=
=cosθ.
化简方向:
切化弦
例6 已知tanθ=2求值:
解:(1)分子分母同除以cosθ
原式=
=1/7.
化简方向:
弦化切
(2)分子“1”换为 “sin2θ +cos2θ”
原式=
=5/3.
例7. 求证:(1)sin4α-cos4α=2sin2α-1;
证明:左边=(sin2α+cos2α)(sin2α-cos2α)
=sin2α-cos2α
=sin2α-(1-sin2α)
=2sin2α-1右边.
所以原等式成立.
(2)
证明:
原式右边=tan2α(1-cos2α)
=tan2α-tan2αcos2α
=tan2α-sin2α
=左边.
(3)
证明:左边
=右边
∴原等式成立.
证明等式的常用方法:
1.从等式的一边证得它等于另一边;
2.先证明另外一个等式成立,从而推出需要
证明的等式成立;
3.利用作差(作商)的方法。
