【数学】1.2.4《 诱导公式》课件(1)(新人教b版必修4)
文档属性
| 名称 | 【数学】1.2.4《 诱导公式》课件(1)(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 46.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
诱导公式(一)
在直角坐标系中,α与α+2kπ(k∈Z)的终边相同,由三角函数的定义,它们的三角函数值相等,
公式(一)
这组公式可以统一概括为的形式,
特征:两边是同名函数,且符号相同.
作用:把任意角的正弦、余弦、正切化为
0 ~360 之间角的正弦、余弦、正切
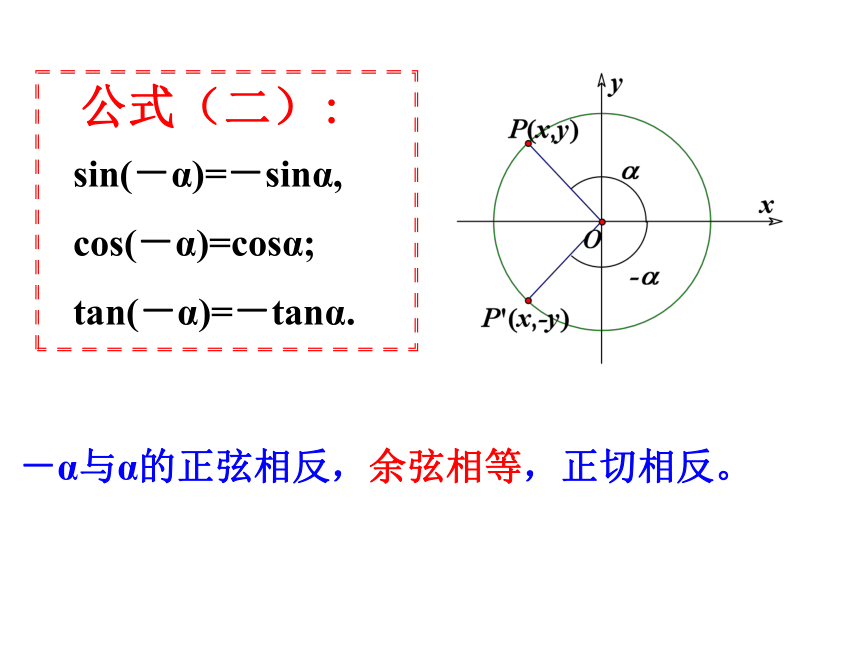
公式(二):
sin(-α)=-sinα,
cos(-α)=cosα;
tan(-α)=-tanα.
-α与α的正弦相反,余弦相等,正切相反。
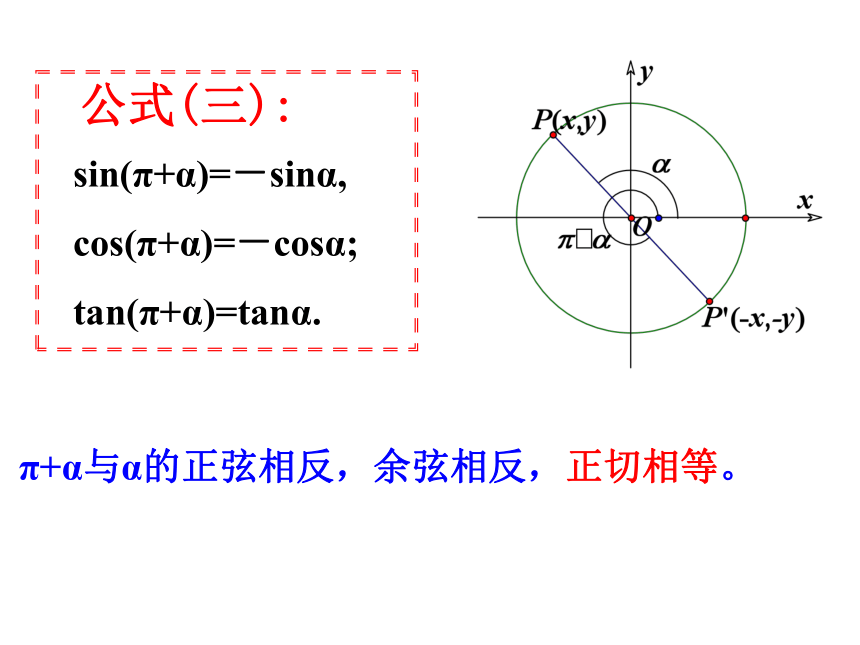
公式(三):
sin(π+α)=-sinα,
cos(π+α)=-cosα;
tan(π+α)=tanα.
π+α与α的正弦相反,余弦相反,正切相等。
公式(四):
sin(π-α)=sinα,
cos(π-α)=-cosα;
tan(π-α)= -tanα.
π-α与α的正弦相等,余弦相反,正切相反。
例1.下列三角函数值:
(1)cos210 ; (2)sin
解:(1)cos210 =cos(180 +30 )
=-cos30
(2)sin =sin(π+ )
=-sin
例2.求下列各式的值:
(1)sin( );(2)cos(-60 )-sin(-210 ).
解:(1)sin(- )
=-sin(π+ )
=sin
=
(2)原式=cos60 +sin(180 +30 )
=cos60 -sin30
=
例3.化简:
解:原式=
=-1.
例4.已知cos(π+α)= , <α<2π,则sin(2π-α)的值是( ).
(A) (B)
(C)- (D)±
A
练习:
1.求下式的值:
2sin(-1110 ) -sin960 + cos(-225 )+cos(-210 )
答案:-2.
提示:
原式=2sin(-30 )+sin60 -
2.化简sin(-2)+cos(-2-π)·tan(2-4π)所得的结果是( )
(A) 2sin2 (B) 0
(C) -2sin2 (D) -1
C
3. 化简: 得( )
A. sin2+cos2 B. cos2-sin2
C. sin2-cos2 D. ±(cos2-sin2)
C
4. 已知sin(π+α)= ,且α是第四象限角,则cos(α-2π)的值是 ( )
(A)- (B)
(C)± (D)
B
诱导公式(一)
在直角坐标系中,α与α+2kπ(k∈Z)的终边相同,由三角函数的定义,它们的三角函数值相等,
公式(一)
这组公式可以统一概括为的形式,
特征:两边是同名函数,且符号相同.
作用:把任意角的正弦、余弦、正切化为
0 ~360 之间角的正弦、余弦、正切
公式(二):
sin(-α)=-sinα,
cos(-α)=cosα;
tan(-α)=-tanα.
-α与α的正弦相反,余弦相等,正切相反。
公式(三):
sin(π+α)=-sinα,
cos(π+α)=-cosα;
tan(π+α)=tanα.
π+α与α的正弦相反,余弦相反,正切相等。
公式(四):
sin(π-α)=sinα,
cos(π-α)=-cosα;
tan(π-α)= -tanα.
π-α与α的正弦相等,余弦相反,正切相反。
例1.下列三角函数值:
(1)cos210 ; (2)sin
解:(1)cos210 =cos(180 +30 )
=-cos30
(2)sin =sin(π+ )
=-sin
例2.求下列各式的值:
(1)sin( );(2)cos(-60 )-sin(-210 ).
解:(1)sin(- )
=-sin(π+ )
=sin
=
(2)原式=cos60 +sin(180 +30 )
=cos60 -sin30
=
例3.化简:
解:原式=
=-1.
例4.已知cos(π+α)= , <α<2π,则sin(2π-α)的值是( ).
(A) (B)
(C)- (D)±
A
练习:
1.求下式的值:
2sin(-1110 ) -sin960 + cos(-225 )+cos(-210 )
答案:-2.
提示:
原式=2sin(-30 )+sin60 -
2.化简sin(-2)+cos(-2-π)·tan(2-4π)所得的结果是( )
(A) 2sin2 (B) 0
(C) -2sin2 (D) -1
C
3. 化简: 得( )
A. sin2+cos2 B. cos2-sin2
C. sin2-cos2 D. ±(cos2-sin2)
C
4. 已知sin(π+α)= ,且α是第四象限角,则cos(α-2π)的值是 ( )
(A)- (B)
(C)± (D)
B
