【数学】1.2.4《诱导公式(2)》课件(新人教b版必修4)
文档属性
| 名称 | 【数学】1.2.4《诱导公式(2)》课件(新人教b版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 72.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 16:11:36 | ||
图片预览






文档简介
(共19张PPT)
1.2.4 诱导公式(二)
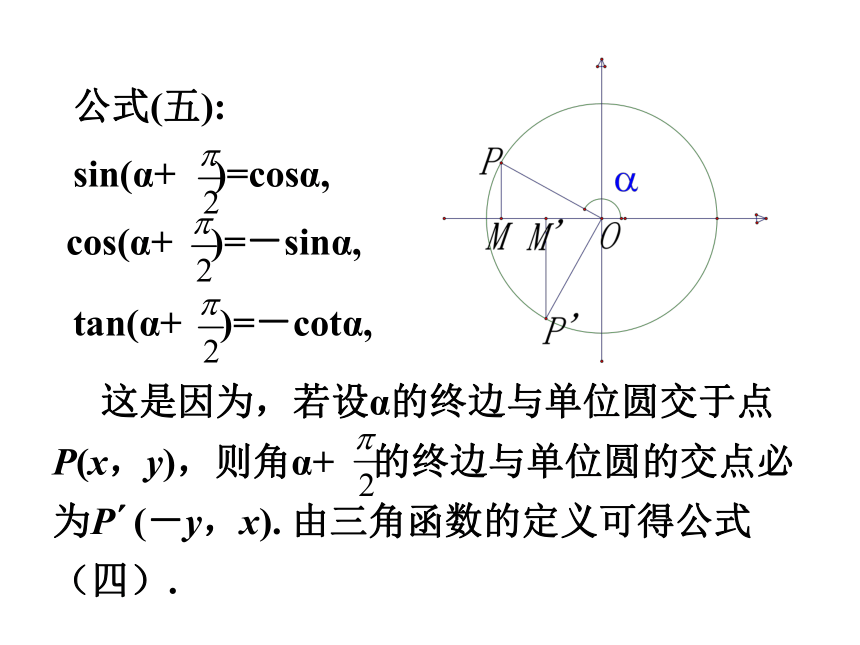
公式(五):
sin(α+ )=cosα,
cos(α+ )=-sinα,
tan(α+ )=-cotα,
这是因为,若设α的终边与单位圆交于点P(x,y),则角α+ 的终边与单位圆的交点必为P (-y,x). 由三角函数的定义可得公式(四).
公式(六):
sin(-α+ )=cosα,
cos(-α+ )=sinα,
tan(-α+ )=cotα,
四组诱导公式的作用 :
任意一个角都可以表示为
的形式。
这样由前面的公式就可以把任意角的三角函数求值问题转化为0到 之间角的三角函数求值问题。
这样,诱导公式可以分为两大组:
(1) 由2kπ+α,-α,π+α,π-α等为一组,所得到的三角函数与原来的三角函数是相同三角函数;
(2)由 +α, -α为一组,所得到的三角函数与原来的三角函数是互余的三角函数;
记忆口诀:奇变偶不变.
所有的诱导公式的符号是由角度所在象限决定的,即把角α看做锐角,原来角度所在象限,原来函数所具有的符号为公式右边的符号。
记忆口诀:符号看象限.
例1 求证:
证:
左边 = 右边 .
∴ 原等式成立 .
例2.
解:
=1.
例3 .已知sinβ= ,sin(α+β)=1,求sin(2α+β).
解:
从而
=sin(π-β)
=sinβ
=
例4. 已知f(cosx)=cos17x,求f(sinx)
解:f(sinx)=f[cos(90 -x)]
=cos[17×(90 -x)]
=cos(4×360 +90 -17x)
=cos(90 -17x)
=sin17x.
课堂练习:
1.计算:sin315 sin( 480 )+cos( 330 ) .
解:原式 = sin(360 45 ) + sin(360 +120 ) + cos( 360 +30 )
= sin45 + sin60 + cos30
2.已知
解:
3.求证:
证:若k是偶数,即k = 2n (n Z) 则:
=-1
若k是奇数,即k = 2n + 1 (n Z) 则:
=-1
∴原式成立.
5.已知:
解:由题设:
由此:当a 0时,tan < 0, cos < 0, 为第二象限角,
当a = 0时,tan = 0, = k , ∴cos = ±1,
∵ cos ≤0, ∴cos = 1 ,
综上所述:
6.若关于x的方程2cos2( + x) sinx + a = 0 有实根,求实数a的取值范围。
解:原方程变形为:2cos2x sinx + a = 0 ,
即 2 2sin2x sinx + a = 0
∴
∵ 1≤sinx≤1
∴
∴ a的取值范围是[ ].
小结: 应用诱导公式化简三角函数的一般步骤:
1 用“ ”公式化为正角的三角函数;
2 用“2k + ”公式化为[0,2 ]角的三角函数;
3 用“ ± ”或“2 ”公式化为锐角的三角函数.
1.2.4 诱导公式(二)
公式(五):
sin(α+ )=cosα,
cos(α+ )=-sinα,
tan(α+ )=-cotα,
这是因为,若设α的终边与单位圆交于点P(x,y),则角α+ 的终边与单位圆的交点必为P (-y,x). 由三角函数的定义可得公式(四).
公式(六):
sin(-α+ )=cosα,
cos(-α+ )=sinα,
tan(-α+ )=cotα,
四组诱导公式的作用 :
任意一个角都可以表示为
的形式。
这样由前面的公式就可以把任意角的三角函数求值问题转化为0到 之间角的三角函数求值问题。
这样,诱导公式可以分为两大组:
(1) 由2kπ+α,-α,π+α,π-α等为一组,所得到的三角函数与原来的三角函数是相同三角函数;
(2)由 +α, -α为一组,所得到的三角函数与原来的三角函数是互余的三角函数;
记忆口诀:奇变偶不变.
所有的诱导公式的符号是由角度所在象限决定的,即把角α看做锐角,原来角度所在象限,原来函数所具有的符号为公式右边的符号。
记忆口诀:符号看象限.
例1 求证:
证:
左边 = 右边 .
∴ 原等式成立 .
例2.
解:
=1.
例3 .已知sinβ= ,sin(α+β)=1,求sin(2α+β).
解:
从而
=sin(π-β)
=sinβ
=
例4. 已知f(cosx)=cos17x,求f(sinx)
解:f(sinx)=f[cos(90 -x)]
=cos[17×(90 -x)]
=cos(4×360 +90 -17x)
=cos(90 -17x)
=sin17x.
课堂练习:
1.计算:sin315 sin( 480 )+cos( 330 ) .
解:原式 = sin(360 45 ) + sin(360 +120 ) + cos( 360 +30 )
= sin45 + sin60 + cos30
2.已知
解:
3.求证:
证:若k是偶数,即k = 2n (n Z) 则:
=-1
若k是奇数,即k = 2n + 1 (n Z) 则:
=-1
∴原式成立.
5.已知:
解:由题设:
由此:当a 0时,tan < 0, cos < 0, 为第二象限角,
当a = 0时,tan = 0, = k , ∴cos = ±1,
∵ cos ≤0, ∴cos = 1 ,
综上所述:
6.若关于x的方程2cos2( + x) sinx + a = 0 有实根,求实数a的取值范围。
解:原方程变形为:2cos2x sinx + a = 0 ,
即 2 2sin2x sinx + a = 0
∴
∵ 1≤sinx≤1
∴
∴ a的取值范围是[ ].
小结: 应用诱导公式化简三角函数的一般步骤:
1 用“ ”公式化为正角的三角函数;
2 用“2k + ”公式化为[0,2 ]角的三角函数;
3 用“ ± ”或“2 ”公式化为锐角的三角函数.
