【数学】1.2.4《诱导公式(3)》课件(新人教b版必修4)
文档属性
| 名称 | 【数学】1.2.4《诱导公式(3)》课件(新人教b版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 81.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 16:11:36 | ||
图片预览


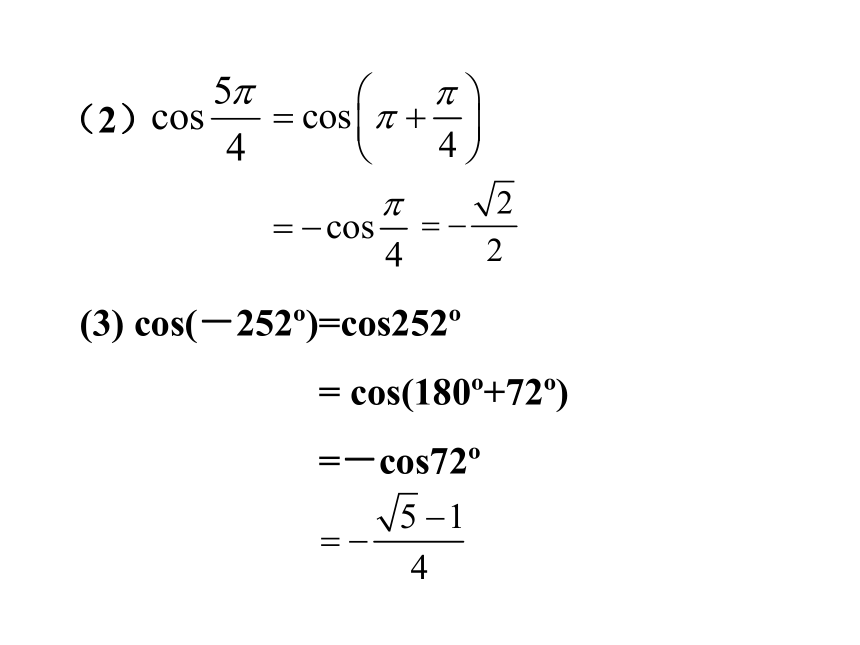




文档简介
(共18张PPT)
1.2.4 诱导公式(三)
四组诱导公式及这四组诱导公式的综合运用.
例1.求下列三角函数的值:
sin240 ; (2) ;
(3) cos(-252 ); (4) sin(- )
解:(1)sin240 =sin(180 +60 )
=-sin60
(2)
(3) cos(-252 )=cos252
= cos(180 +72 )
=-cos72
(4) sin(- )=-sin
=-sin(- )
=sin
例2.求下列三角函数的值:
(1)sin(-119 45′); (2) cos ;
(3)cos(-150 ); (4) sin
解:(1) sin(-119 45’)=-sin119 45’
=-sin(180 -60 15’)
= -sin60 15′
=-08682.
(2) cos =cos( )
=cos
=
(3)cos(-150 )=cos150
=cos(180 -30 )
=-cos30
(4) sin =sin( )
=-sin
例3.求值:
解:原式=-sin -cos -sin
=-sin -cos +sin
=sin +cos +sin
= + +0.3090=13090
例4.化简:
解:原式=
例5.化简:
解:原式=
例6.求证:
证明:左边=
=tan3α=右边,
所以,原式成立.
例7.已知.
求 的值.
解:由已知条件得
又
所以
练习:
1.在△ABC中,若最大角的正弦值是 ,则△ABC必是 ( )
(A)等边三角形 (B)直角三角形
(C)钝角三角形 (D)锐角三角形
C
2. 设A,B,C是三角形的三个内角,下列关系恒等成立的是( )
(A)cos(A+B)=cosC (B)sin(A+B)=sinC (C)tan(A+B)=tanC (D)sin =sin
B
3.化简 = .
1
4.已知f(x)=asin(πx+α)+bcos(πx+β),其中α、β、a、b均为非零常数,且已知
f(2006) = ,则f(2007) = .
5.设f(θ)= ,
求f( )的值.
解:f(θ)=
=cosθ-1
∴f( )=cos -1=-
6.已知cosα= , cos(α+β)=-1,求cos(2α+β)的值.
解:∵cos(α+β)= - 1, ∴α+β=2kπ+π, k∈Z.
∴cos(2α+β)= cos(α+α+β)
= cos(π+α)=-cosα
= -
1.2.4 诱导公式(三)
四组诱导公式及这四组诱导公式的综合运用.
例1.求下列三角函数的值:
sin240 ; (2) ;
(3) cos(-252 ); (4) sin(- )
解:(1)sin240 =sin(180 +60 )
=-sin60
(2)
(3) cos(-252 )=cos252
= cos(180 +72 )
=-cos72
(4) sin(- )=-sin
=-sin(- )
=sin
例2.求下列三角函数的值:
(1)sin(-119 45′); (2) cos ;
(3)cos(-150 ); (4) sin
解:(1) sin(-119 45’)=-sin119 45’
=-sin(180 -60 15’)
= -sin60 15′
=-08682.
(2) cos =cos( )
=cos
=
(3)cos(-150 )=cos150
=cos(180 -30 )
=-cos30
(4) sin =sin( )
=-sin
例3.求值:
解:原式=-sin -cos -sin
=-sin -cos +sin
=sin +cos +sin
= + +0.3090=13090
例4.化简:
解:原式=
例5.化简:
解:原式=
例6.求证:
证明:左边=
=tan3α=右边,
所以,原式成立.
例7.已知.
求 的值.
解:由已知条件得
又
所以
练习:
1.在△ABC中,若最大角的正弦值是 ,则△ABC必是 ( )
(A)等边三角形 (B)直角三角形
(C)钝角三角形 (D)锐角三角形
C
2. 设A,B,C是三角形的三个内角,下列关系恒等成立的是( )
(A)cos(A+B)=cosC (B)sin(A+B)=sinC (C)tan(A+B)=tanC (D)sin =sin
B
3.化简 = .
1
4.已知f(x)=asin(πx+α)+bcos(πx+β),其中α、β、a、b均为非零常数,且已知
f(2006) = ,则f(2007) = .
5.设f(θ)= ,
求f( )的值.
解:f(θ)=
=cosθ-1
∴f( )=cos -1=-
6.已知cosα= , cos(α+β)=-1,求cos(2α+β)的值.
解:∵cos(α+β)= - 1, ∴α+β=2kπ+π, k∈Z.
∴cos(2α+β)= cos(α+α+β)
= cos(π+α)=-cosα
= -
