【数学】1.3.2(1)《余弦函数的图象及性质》课件(新人教b版必修4)
文档属性
| 名称 | 【数学】1.3.2(1)《余弦函数的图象及性质》课件(新人教b版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 88.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 16:11:36 | ||
图片预览








文档简介
(共23张PPT)
1.3.2 余弦函数的图象与性质
利用五点描图法画出y=sinx的图象,
图象向两边延伸,得
1. 余弦函数的图象
把函数y=sinx的图象,向左平移 单位即得到y=cosx的图象 。
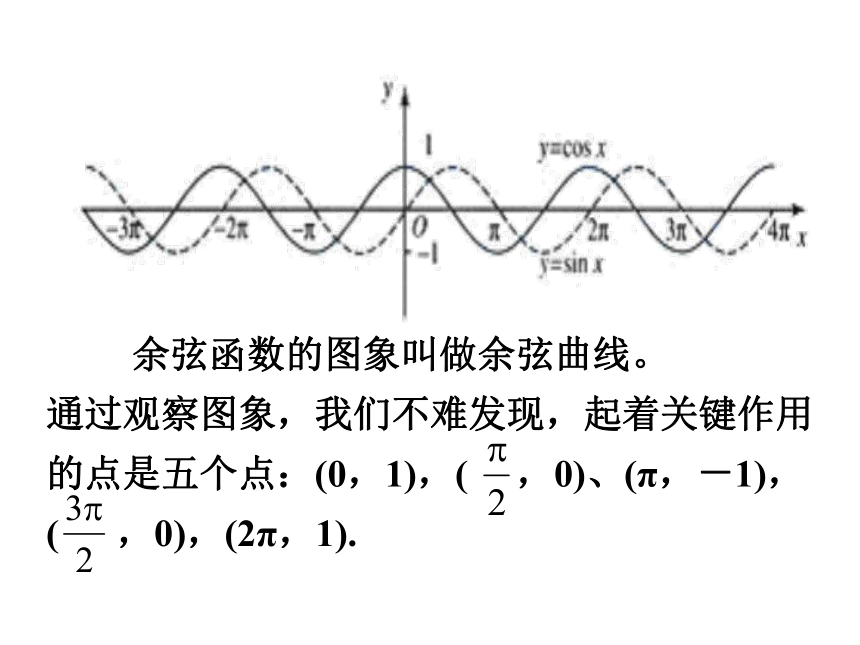
余弦函数的图象叫做余弦曲线。
通过观察图象,我们不难发现,起着关键作用的点是五个点:(0,1),( ,0)、(π,-1),( ,0),(2π,1).
2. 余弦函数的性质:
(1) 定义域: y=cosx的定义域为R
(2) 值域:
① 由单位圆中的三角函数线,得结论: |cosx|≤1 (有界性)
再看正弦函数线(图象)验证上述结论:
所以y=cosx的值域为[-1,1];
②对于y=cosx
当且仅当x=2k k Z时 ymax=1,
当且仅当x=2k + k Z时 ymin=-1,
③观察R上的y=cosx的图象可知
当2k -0
当2k +(3).周期性:(观察图象)
①余弦函数的图象是有规律不断重复出现的;
②规律是:每隔2 重复出现一次(或者说每隔2k ,k Z重复出现)
③这个规律由诱导公式 cos(2k +x)=cosx也可以说明余弦函数的最小正周期是T=2π.
(4). 奇偶性
由诱导公式:cos(-x)=cosx 得余弦函数是偶函数。
(5).单调性
余弦函数在每一个闭区间[2kπ, 2kπ+π], k∈Z上是减函数;
在每一个闭区间[2kπ+π, 2kπ+2π],k∈Z上是增函数。
例1、求下列函数的最值:
(1)y=-3cosx+1;
(2)
解:(1) ∵ -1≤cosx≤1,
∴ -2≤-3cosx+1≤4.
即ymax=4,ymin= -2.
(3)
(2)
解:(2) ∵ -1≤cosx≤1,
当cosx=-1时,ymax=
∴ 当cosx= 时,ymin=-3,
(3)
解:因为cosx∈[-1, 1],所以cos2x∈[0,1].
当cosx=0时,ymax=1;
当cosx=1或cosx=-1时,ymin=
例2、判断下列函数的奇偶性:
(1)y=cosx+2;
(2)y=cosxsinx.
解:(1)f(-x)=cos(-x)+2
=cosx+2=f(x),
∴ 函数y=cosx+2是偶函数.
(2) f(-x)=cos(-x)sin(-x)
=-cosxsinx=-f(x).
∴ 函数y=cosxsinx是奇函数.
例3、求函数 的最小正周期.
解:因为
∴ 原函数的最小正周期是6π.
例4、求函数 的单调区间。
解:当 时,
即 时,原函数为减函数;
当 时,
即 时,原函数为增函数;
例5. 下列各题中,两个函数的图象之间有什么关系?
(1)y=2cosx与y=cosx;
(2)y=cos2x与y=cosx;
(3) 与y=cosx;
(4) 与y=cosx.
练习
1.下列说法中不正确的是 ( )
(A) 正弦函数、余弦函数的定义域都是R,值域都是[-1,1];
(B) 余弦函数当且仅当x=2kπ( k∈Z) 时,取得最大值1;
(C) 余弦函数在[2kπ+ ,2kπ+ ]( k∈Z)上都是减函数;
(D) 余弦函数在[2kπ-π, 2kπ]( k∈Z)上都是减函数
C
2.函数f(x)=cosx-|cosx|的值域为 ( )
(A){0} (B) [-1,1] (C) [0,1] (D) [-2,0]
D
3.若a=sin46° , b=cos46°, c=cos36°,则a、b、c的大小关系是 ( )
(A) c> a > b (B) a > b> c (C) a >c> b (D) b> c> a
A
4. 对于函数y=sin( π-x),下面说法中正确的是 ( )
函数是周期为π的奇函数
(B) 函数是周期为π的偶函数
(C) 函数是周期为2π的奇函数
(D) 函数是周期为2π的偶函数
D
5.函数y=2cosx(0≤x≤2π)的图象和直线y=2围成一个封闭的平面图形,则这个封闭图形的面积是( )
4 (B) 8
(C) 2π (D) 4π
D
6. 函数值sin1,sin2,sin3,sin4的大小顺序是 .
sin2>sin1>sin3>sin4
7. 函数y=cos(sinx)的奇偶性是 .
偶函数
8. 函数f(x)=lg(2sinx+1)+ 的定义域是 ;
2kπ-9.关于x的方程cos2x+sinx-a=0有实数解,则实数a的最小值是 .
-1
10. 已知函数y= f(x)的定义域是[0, ],求函数y=f(sin2x) 的定义域.
解:由0≤sin2x≤ ,即- ≤sinx≤ 得:
kπ- ≤x≤kπ+ , ( k∈Z)
11.已知y=a-bcos3x的最大值为 ,最小值为 ,求实数a与b的值.
解:当b>0时,有
解得
当b<0时, 有
解得
1.3.2 余弦函数的图象与性质
利用五点描图法画出y=sinx的图象,
图象向两边延伸,得
1. 余弦函数的图象
把函数y=sinx的图象,向左平移 单位即得到y=cosx的图象 。
余弦函数的图象叫做余弦曲线。
通过观察图象,我们不难发现,起着关键作用的点是五个点:(0,1),( ,0)、(π,-1),( ,0),(2π,1).
2. 余弦函数的性质:
(1) 定义域: y=cosx的定义域为R
(2) 值域:
① 由单位圆中的三角函数线,得结论: |cosx|≤1 (有界性)
再看正弦函数线(图象)验证上述结论:
所以y=cosx的值域为[-1,1];
②对于y=cosx
当且仅当x=2k k Z时 ymax=1,
当且仅当x=2k + k Z时 ymin=-1,
③观察R上的y=cosx的图象可知
当2k -
当2k +
①余弦函数的图象是有规律不断重复出现的;
②规律是:每隔2 重复出现一次(或者说每隔2k ,k Z重复出现)
③这个规律由诱导公式 cos(2k +x)=cosx也可以说明余弦函数的最小正周期是T=2π.
(4). 奇偶性
由诱导公式:cos(-x)=cosx 得余弦函数是偶函数。
(5).单调性
余弦函数在每一个闭区间[2kπ, 2kπ+π], k∈Z上是减函数;
在每一个闭区间[2kπ+π, 2kπ+2π],k∈Z上是增函数。
例1、求下列函数的最值:
(1)y=-3cosx+1;
(2)
解:(1) ∵ -1≤cosx≤1,
∴ -2≤-3cosx+1≤4.
即ymax=4,ymin= -2.
(3)
(2)
解:(2) ∵ -1≤cosx≤1,
当cosx=-1时,ymax=
∴ 当cosx= 时,ymin=-3,
(3)
解:因为cosx∈[-1, 1],所以cos2x∈[0,1].
当cosx=0时,ymax=1;
当cosx=1或cosx=-1时,ymin=
例2、判断下列函数的奇偶性:
(1)y=cosx+2;
(2)y=cosxsinx.
解:(1)f(-x)=cos(-x)+2
=cosx+2=f(x),
∴ 函数y=cosx+2是偶函数.
(2) f(-x)=cos(-x)sin(-x)
=-cosxsinx=-f(x).
∴ 函数y=cosxsinx是奇函数.
例3、求函数 的最小正周期.
解:因为
∴ 原函数的最小正周期是6π.
例4、求函数 的单调区间。
解:当 时,
即 时,原函数为减函数;
当 时,
即 时,原函数为增函数;
例5. 下列各题中,两个函数的图象之间有什么关系?
(1)y=2cosx与y=cosx;
(2)y=cos2x与y=cosx;
(3) 与y=cosx;
(4) 与y=cosx.
练习
1.下列说法中不正确的是 ( )
(A) 正弦函数、余弦函数的定义域都是R,值域都是[-1,1];
(B) 余弦函数当且仅当x=2kπ( k∈Z) 时,取得最大值1;
(C) 余弦函数在[2kπ+ ,2kπ+ ]( k∈Z)上都是减函数;
(D) 余弦函数在[2kπ-π, 2kπ]( k∈Z)上都是减函数
C
2.函数f(x)=cosx-|cosx|的值域为 ( )
(A){0} (B) [-1,1] (C) [0,1] (D) [-2,0]
D
3.若a=sin46° , b=cos46°, c=cos36°,则a、b、c的大小关系是 ( )
(A) c> a > b (B) a > b> c (C) a >c> b (D) b> c> a
A
4. 对于函数y=sin( π-x),下面说法中正确的是 ( )
函数是周期为π的奇函数
(B) 函数是周期为π的偶函数
(C) 函数是周期为2π的奇函数
(D) 函数是周期为2π的偶函数
D
5.函数y=2cosx(0≤x≤2π)的图象和直线y=2围成一个封闭的平面图形,则这个封闭图形的面积是( )
4 (B) 8
(C) 2π (D) 4π
D
6. 函数值sin1,sin2,sin3,sin4的大小顺序是 .
sin2>sin1>sin3>sin4
7. 函数y=cos(sinx)的奇偶性是 .
偶函数
8. 函数f(x)=lg(2sinx+1)+ 的定义域是 ;
2kπ-
-1
10. 已知函数y= f(x)的定义域是[0, ],求函数y=f(sin2x) 的定义域.
解:由0≤sin2x≤ ,即- ≤sinx≤ 得:
kπ- ≤x≤kπ+ , ( k∈Z)
11.已知y=a-bcos3x的最大值为 ,最小值为 ,求实数a与b的值.
解:当b>0时,有
解得
当b<0时, 有
解得
