【数学】1.3.3《已知三角函数值求角》 课件(新人教b版必修4)
文档属性
| 名称 | 【数学】1.3.3《已知三角函数值求角》 课件(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 147.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
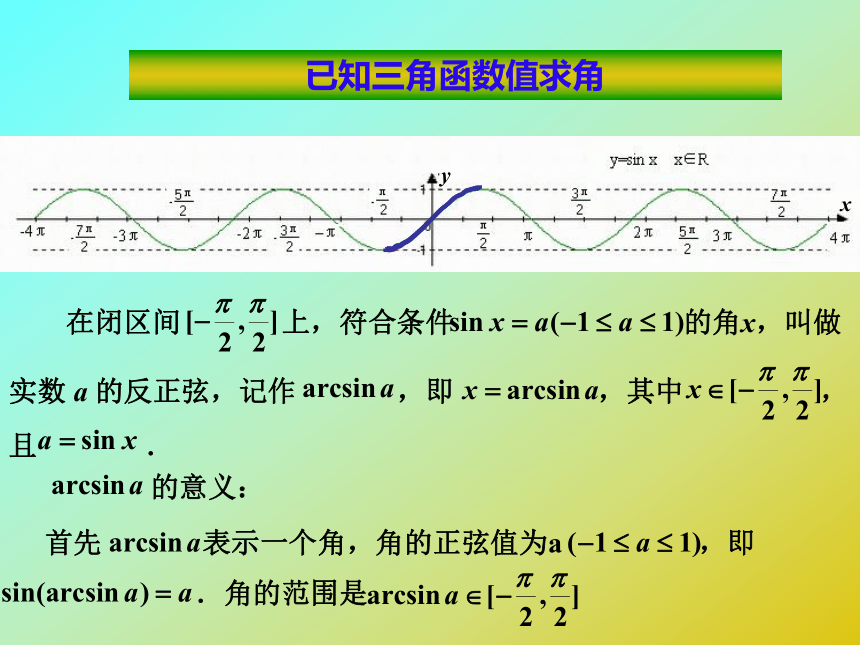
已知三角函数值求角
回忆:
,
,
,
的诱导公式.
已知角
三角函数值
解唯一
已知三角函数值
角
角的范围决定解的个数
例1. (1)已知 ,且 ,求x;
(2)已知 ,且 ,求x的取值集合.
解:
(1)由于正弦函数在闭区间 上是增函数和
可知符合条件的角有且只有一个,即 .
于是
(2)因为 ,所以x是第一或第二象限角.
由正弦函数的单调性和
可知符合条件的角有且只有两个,即第一象限角 或
第二象限角
所以x的集合是
已知三角函数值求角
y
x
根据正弦函数的图象和性质寻找区间使其满足:
使符合条件的 的角x有且只有一个,而且包括锐角.
在闭区间 上,符合条件 的角x,叫做
实数 a 的反正弦,记作 ,即 ,其中 ,
且 .
的意义:
首先 表示一个角,角的正弦值为a ,即
.角的范围是
已知三角函数值求角
练习:
(1) 表示什么意思?
表示 上正弦值等于 的那个角,即角 ,
故
(2)若
,则x=
(3)若
,则x=
已知三角函数值求角
可知符合条件的角有且只有一个,
而且角为钝角,
解:
(1)由于余弦函数在闭区间 上是减函数和
例2. (1)已知 ,且 ,求x.
(2)已知 ,且 ,求x 的取值集合.
可得
,所以
利用计算器并由:
(2)因为 ,所以x是第二象限或第三
象限角.
故x 的集合是
可知符合条件的角有且只有两个,即第二象限角 或
第三象限角
由余弦函数的单调性和
已知三角函数值求角
的意义:
首先 表示一个角,角的余弦值为a ,即
.角的范围是 .
根据余弦函数的图象和性质寻找区间使其满足:
使符合条件的 的角x有且只有一个,而且包括锐角.
y
x
在闭区间 上,符合条件 的角x,叫做
实数 a 的反余弦,记作 ,即 ,其中 ,
且 .
已知三角函数值求角
练习:
(1)已知 , ,求x.
(2)已知 , ,求x的取值集合.
(3)已知 , ,求x的取值集合
已知三角函数值求角
例3. (1)已知 ,且 ,求x(用弧度表示).
(2)已知 ,且 ,求x的取值集合.
解:
(1)利用计算器并由
可得
,所以 (或 )
已知三角函数值求角
(2)由正弦函数的单调性和
(2)已知 ,且 ,求x的取值集合.
解:
可知 角, 角的正弦也是-0.3322,
所以x的取值集合是
或
已知三角函数值求角
练习:
(1)若 ,则x的值( )
(2)若 ,集合 且
,则x的值为
B
已知三角函数值求角
1. 表示一个角,角的正弦值为a ,即
角的范围是
2. 表示一个角,角的余弦值为a ,即
.角的范围是 .
已知三角函数值求角
你都学
会了么?
已知三角函数值求角
回忆:
,
,
,
的诱导公式.
已知角
三角函数值
解唯一
已知三角函数值
角
角的范围决定解的个数
例1. (1)已知 ,且 ,求x;
(2)已知 ,且 ,求x的取值集合.
解:
(1)由于正弦函数在闭区间 上是增函数和
可知符合条件的角有且只有一个,即 .
于是
(2)因为 ,所以x是第一或第二象限角.
由正弦函数的单调性和
可知符合条件的角有且只有两个,即第一象限角 或
第二象限角
所以x的集合是
已知三角函数值求角
y
x
根据正弦函数的图象和性质寻找区间使其满足:
使符合条件的 的角x有且只有一个,而且包括锐角.
在闭区间 上,符合条件 的角x,叫做
实数 a 的反正弦,记作 ,即 ,其中 ,
且 .
的意义:
首先 表示一个角,角的正弦值为a ,即
.角的范围是
已知三角函数值求角
练习:
(1) 表示什么意思?
表示 上正弦值等于 的那个角,即角 ,
故
(2)若
,则x=
(3)若
,则x=
已知三角函数值求角
可知符合条件的角有且只有一个,
而且角为钝角,
解:
(1)由于余弦函数在闭区间 上是减函数和
例2. (1)已知 ,且 ,求x.
(2)已知 ,且 ,求x 的取值集合.
可得
,所以
利用计算器并由:
(2)因为 ,所以x是第二象限或第三
象限角.
故x 的集合是
可知符合条件的角有且只有两个,即第二象限角 或
第三象限角
由余弦函数的单调性和
已知三角函数值求角
的意义:
首先 表示一个角,角的余弦值为a ,即
.角的范围是 .
根据余弦函数的图象和性质寻找区间使其满足:
使符合条件的 的角x有且只有一个,而且包括锐角.
y
x
在闭区间 上,符合条件 的角x,叫做
实数 a 的反余弦,记作 ,即 ,其中 ,
且 .
已知三角函数值求角
练习:
(1)已知 , ,求x.
(2)已知 , ,求x的取值集合.
(3)已知 , ,求x的取值集合
已知三角函数值求角
例3. (1)已知 ,且 ,求x(用弧度表示).
(2)已知 ,且 ,求x的取值集合.
解:
(1)利用计算器并由
可得
,所以 (或 )
已知三角函数值求角
(2)由正弦函数的单调性和
(2)已知 ,且 ,求x的取值集合.
解:
可知 角, 角的正弦也是-0.3322,
所以x的取值集合是
或
已知三角函数值求角
练习:
(1)若 ,则x的值( )
(2)若 ,集合 且
,则x的值为
B
已知三角函数值求角
1. 表示一个角,角的正弦值为a ,即
角的范围是
2. 表示一个角,角的余弦值为a ,即
.角的范围是 .
已知三角函数值求角
你都学
会了么?
