【数学】2.1.2《向量的加法》课件(新人教b版必修4)
文档属性
| 名称 | 【数学】2.1.2《向量的加法》课件(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 430.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
2.1.2 向量的加法
生活中有向量 生活中用向量
上海
香港
台北
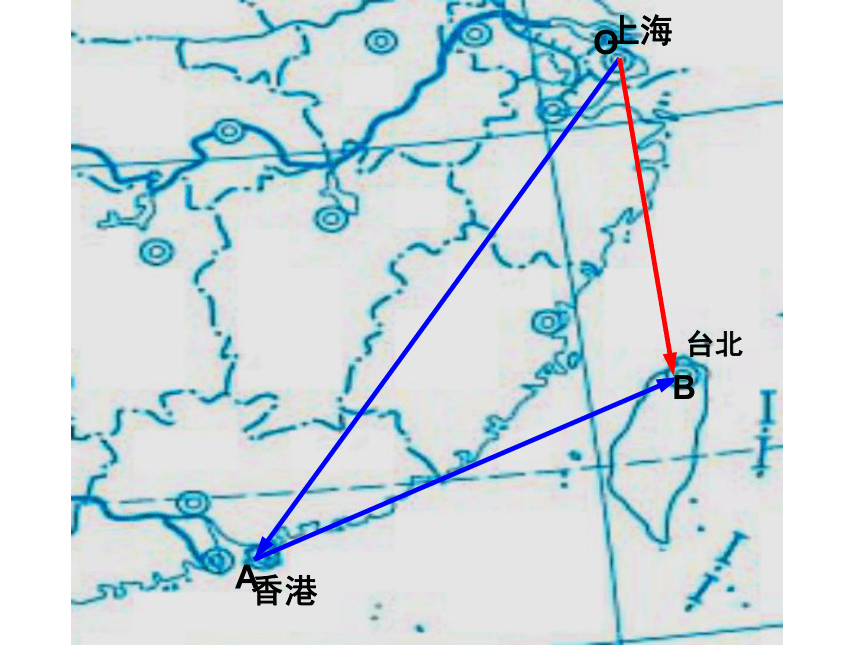
上海
香港
台北
O
A
B
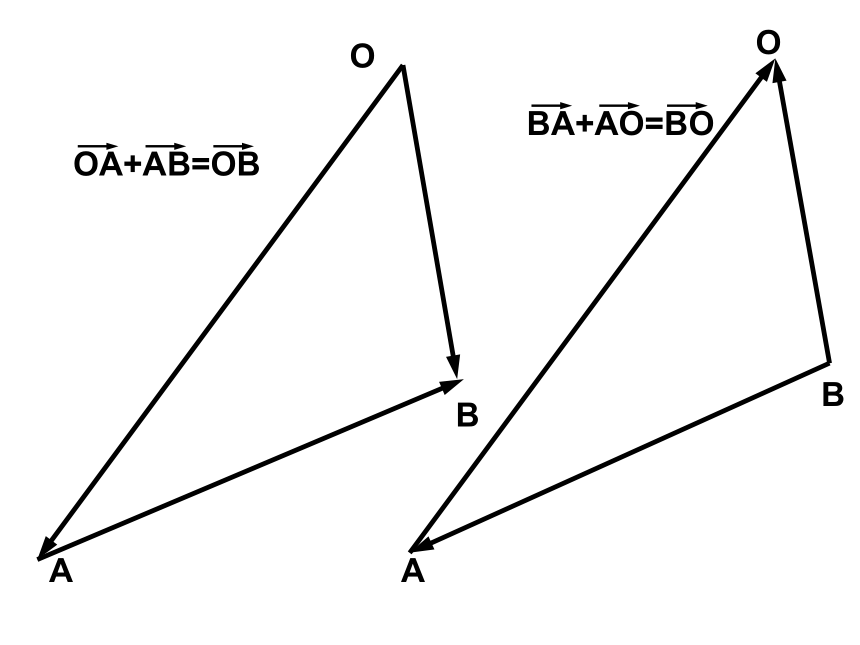
BA+AO=BO
O
A
B
O
A
B
OA+AB=OB
O
A
B
a
b
a+b
a
b
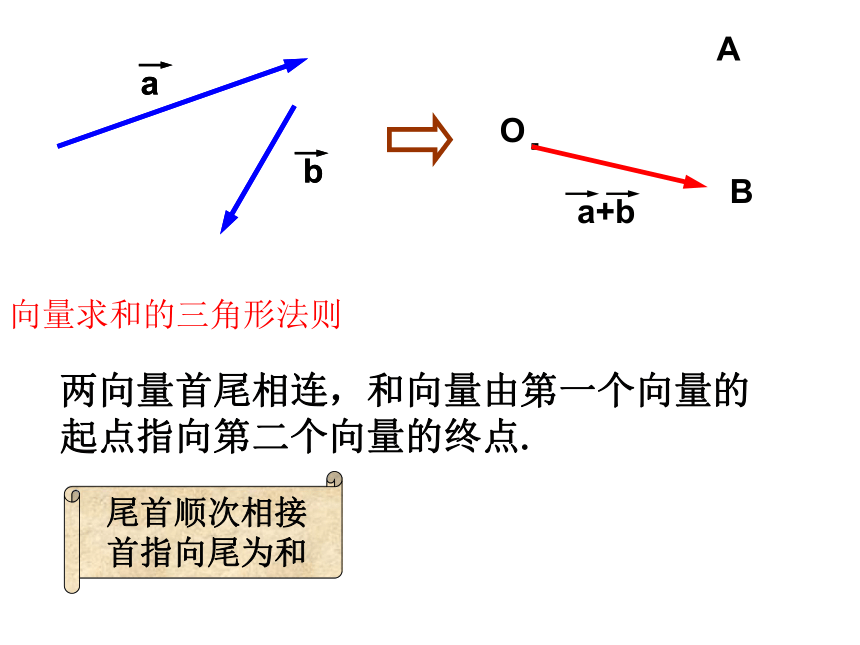
向量求和的三角形法则
两向量首尾相连,和向量由第一个向量的起点指向第二个向量的终点.
尾首顺次相接
首指向尾为和
向量和的特点:
(1)两个向量的和仍是一个_______.
向量
(2).当向量 a 与 b 不共线时,则 向量 a + b ,
a , b 不同向,且/a+b/(3)零向量和任一向量 a 的和是什么
规定:
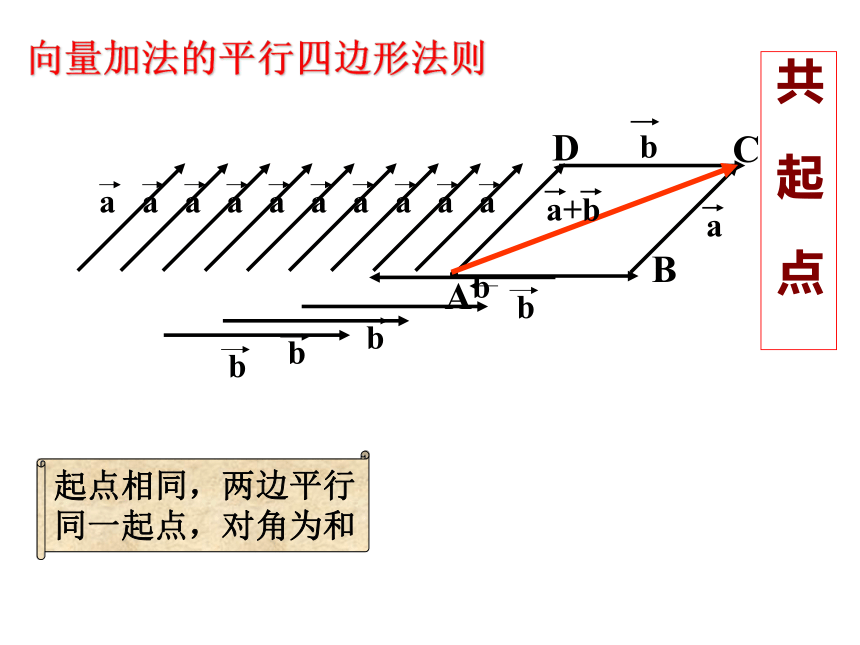
向量加法的平行四边形法则
b
a
A
a
a
a
a
a
a
a
a
b
b
b
B
b
a
D
a
C
b
a+b
共 起 点
起点相同,两边平行
同一起点,对角为和
两种特例(两向量平行)
A
B
C
方向相同
方向相反
C
A
B
▲当向量 a 与 b 同向时,
则向量 a+b , a , b同向,且 /a+b/=/a/+/b/
▲当向量 a 与 b 反向时,若 /a/>/b/ ,
则向量 a + b的方向与 a 相同,且/a+b/=/a/ - /b/
若/a/且/a+b/=/b/ - /a/
a
b
a
b
a+b=AC
a+b=AC
注意:
(1)三角形法则对于两个向量共线时也适用.
(2)两个向量的和向量仍是一个向量.
两个向量的和向量的作法:
A
B
C
1. 三角形法则:
2. 平行四边形法则:
注意:平行四边形法则对于两个向量共线时不适用。
思考:两种方法作出的和向量是否一致?
注1:两种法则具有一致性.
注2:平行四边形法则对于两个向量共线的情况不适用.
b
a
b
a
+
a
b
b
a
+
b
a
c
+
a
b
+
(
)
a
+
b
c
+
(
)
,
.
a
如图,已知 , , ,请作出
b
c
a
b
+
a
b
+
c
b
+
,
,
b
a
c
c
例1:
a+b
b+c
向量加法的运算律
交换律:
结合律:
1.化简
2.根据图示填空
A
B
D
E
C
A1
A2
A3
A1A2+A2A3=_______
探究
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A3
A1A4
向量求和的多边形法则
练习
1.已知A、B、C、D是平面上的任意四点,则
AB+BC+CD=________;DB+BD+AC=__________.
2.ΔABC中,D、 E、 F分别是边AB、BC、AC的中点,则下面结论正确的是( )
AE=AD+FA
DE+AF=0
AB+BC+CA≠0
AB+BC+AC≠0
AD
AC
D
A
B
C
D
E
F
3. O为正六边形A1A2A3A4A5A6的中心,求出
下列向量:
(1)OA1+OA3;
(2)A2A3+A6A5;
(3)OA1+A6A5.
A1
A2
A3
A4
A5
A6
O
(4) A1A2+A2A3+A3A4+A4A5+A5A6+A6A1
小结:
1.向量的加法运算:
O
A
B
三角形法则
O
A
B
C
平行四边形法则
注意:当两向量共线时,三角形法则适用,而平行四边形不再适用.
2.1.2 向量的加法
生活中有向量 生活中用向量
上海
香港
台北
上海
香港
台北
O
A
B
BA+AO=BO
O
A
B
O
A
B
OA+AB=OB
O
A
B
a
b
a+b
a
b
向量求和的三角形法则
两向量首尾相连,和向量由第一个向量的起点指向第二个向量的终点.
尾首顺次相接
首指向尾为和
向量和的特点:
(1)两个向量的和仍是一个_______.
向量
(2).当向量 a 与 b 不共线时,则 向量 a + b ,
a , b 不同向,且/a+b/(3)零向量和任一向量 a 的和是什么
规定:
向量加法的平行四边形法则
b
a
A
a
a
a
a
a
a
a
a
b
b
b
B
b
a
D
a
C
b
a+b
共 起 点
起点相同,两边平行
同一起点,对角为和
两种特例(两向量平行)
A
B
C
方向相同
方向相反
C
A
B
▲当向量 a 与 b 同向时,
则向量 a+b , a , b同向,且 /a+b/=/a/+/b/
▲当向量 a 与 b 反向时,若 /a/>/b/ ,
则向量 a + b的方向与 a 相同,且/a+b/=/a/ - /b/
若/a/且/a+b/=/b/ - /a/
a
b
a
b
a+b=AC
a+b=AC
注意:
(1)三角形法则对于两个向量共线时也适用.
(2)两个向量的和向量仍是一个向量.
两个向量的和向量的作法:
A
B
C
1. 三角形法则:
2. 平行四边形法则:
注意:平行四边形法则对于两个向量共线时不适用。
思考:两种方法作出的和向量是否一致?
注1:两种法则具有一致性.
注2:平行四边形法则对于两个向量共线的情况不适用.
b
a
b
a
+
a
b
b
a
+
b
a
c
+
a
b
+
(
)
a
+
b
c
+
(
)
,
.
a
如图,已知 , , ,请作出
b
c
a
b
+
a
b
+
c
b
+
,
,
b
a
c
c
例1:
a+b
b+c
向量加法的运算律
交换律:
结合律:
1.化简
2.根据图示填空
A
B
D
E
C
A1
A2
A3
A1A2+A2A3=_______
探究
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A3
A1A4
向量求和的多边形法则
练习
1.已知A、B、C、D是平面上的任意四点,则
AB+BC+CD=________;DB+BD+AC=__________.
2.ΔABC中,D、 E、 F分别是边AB、BC、AC的中点,则下面结论正确的是( )
AE=AD+FA
DE+AF=0
AB+BC+CA≠0
AB+BC+AC≠0
AD
AC
D
A
B
C
D
E
F
3. O为正六边形A1A2A3A4A5A6的中心,求出
下列向量:
(1)OA1+OA3;
(2)A2A3+A6A5;
(3)OA1+A6A5.
A1
A2
A3
A4
A5
A6
O
(4) A1A2+A2A3+A3A4+A4A5+A5A6+A6A1
小结:
1.向量的加法运算:
O
A
B
三角形法则
O
A
B
C
平行四边形法则
注意:当两向量共线时,三角形法则适用,而平行四边形不再适用.
