人教版八年级上册数学13.2画轴对称图形第2课时课件(共25张PPT)
文档属性
| 名称 | 人教版八年级上册数学13.2画轴对称图形第2课时课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 165.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 12:28:15 | ||
图片预览



文档简介
(共25张PPT)
第十三章
轴对称
13.2
画轴对称图形
第2课时
1
.理解在平面直角坐标系中,已知点关于x轴或y轴对称的点的坐标的变化规律.培语言表达能力、观察能和归纳能力.
2
.掌握在平面直角坐标系中作出一个图形的轴对称图形的方法.加深对轴对称的理解和掌握.
学习目标
情境导入
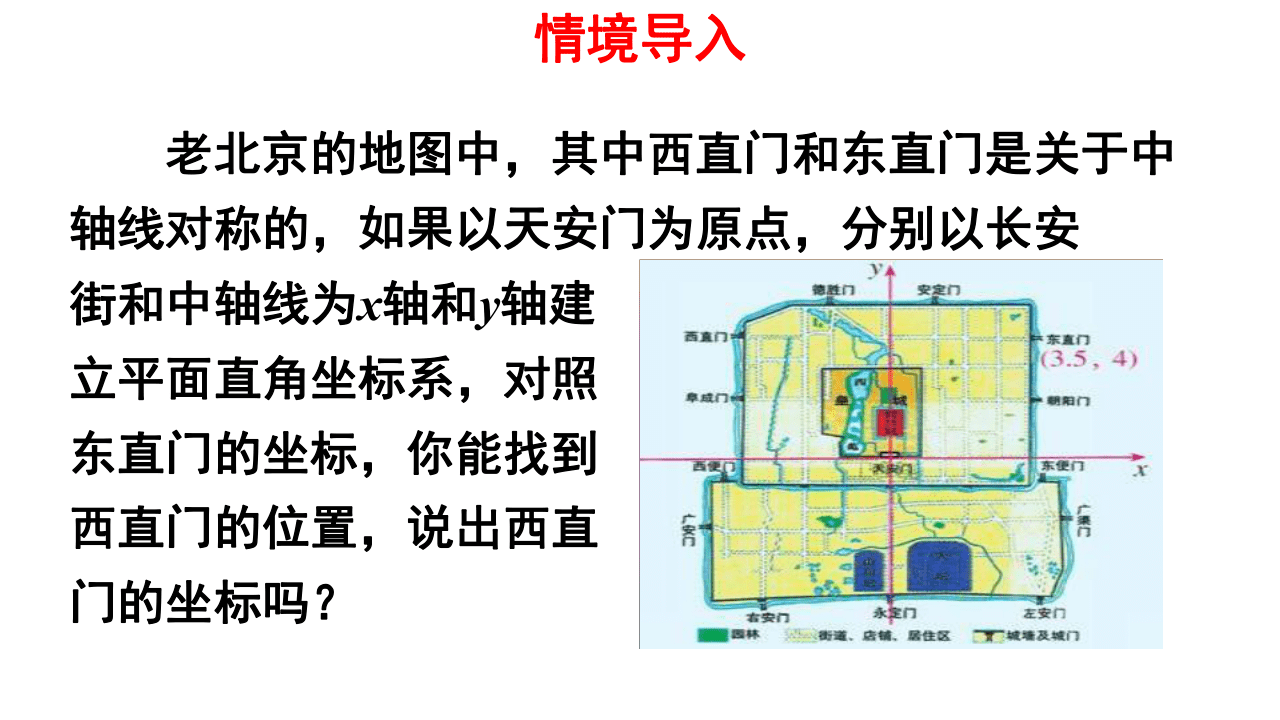
老北京的地图中,其中西直门和东直门是关于中轴线对称的,如果以天安门为原点,分别以长安
街和中轴线为x轴和y轴建
立平面直角坐标系,对照
东直门的坐标,你能找到
西直门的位置,说出西直
门的坐标吗?
用坐标表示轴对称,可以很方便地确定一个地方的位置,实际上在我们日常生活中应用非常广泛,如工程建设的绘图等.这节课我们就来学习用坐标表示轴对称.
情境导入
x
y
1
1
O
A
B
C
E
D
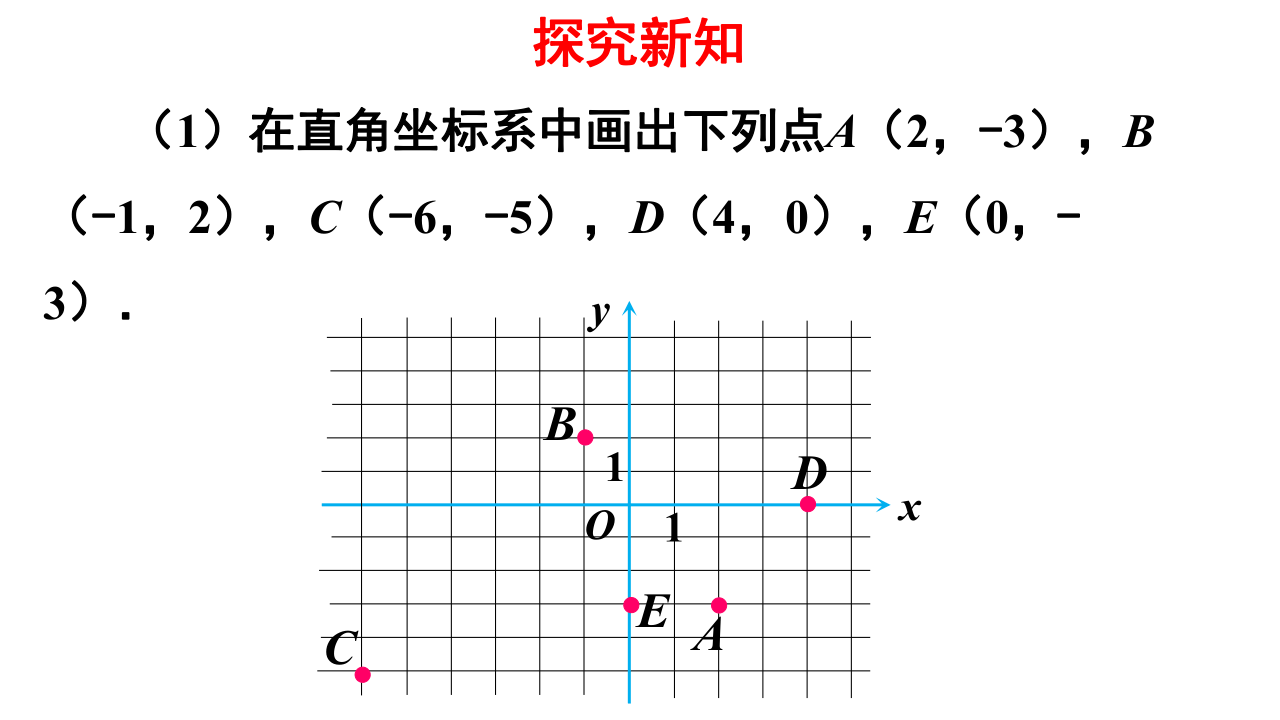
(1)在直角坐标系中画出下列点A(2,-3),B
(-1,2),C(-6,-5),D(4,0),E(0,-3).
探究新知
(2)画出这些点分别关于x轴、y轴对称的点,并填写表格.
(3)请你仔细观察点的坐标,你能发现关于坐标轴对称的点的坐标有什么规律吗?
(4)请你想办法检验你所发现的规律的正确性,并说说你是如何检验的.
关于x轴、y轴对称的点的坐标规律
在平面直角坐标系中,画出下列已知点关于x
轴对称的点,把它们的坐标填入表格中.
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(4,0)
E(0,-3)
关于x轴的对称点
关于x轴、y轴对称的点的坐标规律
C′
A′
x
y
1
1
O
A
B
C
E
D
D′
B′
E′
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(4,0)
E(0,-3)
关于x轴的对称点
A′(2,3)
B′(-1,-2)
C′(-6,5)
D′(4,0)
E′(0,3)
关于x轴、y轴对称的点的坐标规律
关于x
轴对称的每对对称点的横坐标相等,纵坐标互为相反数.
观察下图中关于x
轴对称的每对对称点的坐标有怎样的变化规律?
C′
A′
x
y
1
1
O
A
B
C
E
D
D′
B′
E′
关于x轴、y轴对称的点的坐标规律
在平面直角坐标系中,画出下列已知点关于y
轴对称的点,把它们的坐标填入表格中.
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(4,0)
E(0,-3)
关于y轴的对称点
关于x轴、y轴对称的点的坐标规律
x
y
1
1
O
A
B
C
E
D
A〞
B〞
C〞
E〞
D〞
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(4,0)
E(0,-3)
关于y轴的对称点
A′′(-2,-3)
B′′(1,2)
C′′(6,-5)
D′′(-4,0)
E′′(0,-3)
关于x轴、y轴对称的点的坐标规律
观察关于y
轴对称的每对对称点的坐标有怎样的变化规律?
关于y
轴对称的每对对称点的横坐标互为相反数,纵坐标相等.
x
y
1
1
O
A
B
C
E
D
A〞
B〞
C〞
E〞
D〞
关于x轴、y轴对称的点的坐标规律
再找几个点,检验一下你发现的规律.
点(x,y)关于x
轴对称的点的坐标为(___,___);
点(x,y)关于y
轴对称的点的坐标为(___,___).
x
-y
-x
y
x
y
1
1
O
x
y
1
1
O
关于x轴、y轴对称的点的坐标规律
【例】如图,四边形ABCD
的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD
关
于x
轴和y
轴对称的图形.
x
y
1
1
O
A
B
C
D
例题解析
解:点(x,y)关于y
轴对称的点的坐标为(-x,y),因此四边形ABCD
的顶点A,B,C,D
关于y
轴对称
的点分别为:
A′(
,
),
B′(
,
),
C′(
,
),
D′(
,
),
x
y
1
1
O
A
B
C
D
2
5
5
1
2
1
5
4
A′
B′
C′
D′
例题解析
解:依次连接
,
,
,
,
就可得到与四边形ABCD
关于y轴对称的四边形
.
x
y
1
1
O
A
B
C
D
A′B′C′D′
A′B′
B′C′
C′D′
D′A′
A′
B′
C′
D′
例题解析
解:点(x,y)关于x
轴对称的点的坐标为(-x,y),因此四边形ABCD
的顶点A,B,C,D
关于x
轴对称
的点分别为:
A′′(
,
),
B′′
(
,
),
C′′(
,
),
D′′(
,
),
x
y
1
1
O
A
B
C
D
D′′
C′′
B′′
A′′
-2
-5
-5
-1
-2
-1
-5
-4
例题解析
解:依次连接
,
,
,
,
就可得到与四边形ABCD
关于x轴对称的四边形
.
x
y
1
1
O
A
B
C
D
D′′
C′′
B′′
A′′
A′′B′′C
′′
D
′′
A′′B′′
B′′C′′
C′′D′′
D′′A′′
例题解析
先求出已知图形中一些特殊点(多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
简记为:
(1)求特殊点的坐标;(2)描点;(3)连线.
画一个图形关于x
轴或y
轴对称的图形的方法和步骤.
方法小结
1.分别写出下列各点关于x
轴和y
轴对称的点的坐标:(-2,6),(1,-2),(-1,3),(-4,-2),(1,0)
.
解:关于x
轴对称的点的坐标:(-2,-6),
(1,2),(-1,-3),(-4,2),(1,0).
关于y
轴对称的点的坐标:(2,6),(-1,-2),
(1,3),(4,-2),(-1,0).
课堂练习
2.若点P(2a+b,-3a)与点P′(8,b+2)
关于x
轴对称,则a=
,b=
;
若关于y
轴对称,则a=
,b=_____.
4
-20
2
6
课堂练习
3.以正方形ABCD
的中心为原点建立平面直角坐标系.点A
的坐标为(1,1),写出点B,C,D
的坐标.
A
(1,1)
B
C
D
O
y
x
B(1,-1)
C(-1,-1)
D(-1,1)
课堂练习
4.已知点(3,2)(6,5)(-3,4)(
-3,
-2).
(1)分别写出关于原点对称的点;
(-3,-2)(-6,-5)(3,-4)(3,2)
(2)分别写出关于一、三象限角平分线的
对称点;
(2,3)(5,6)(4,-3)(-2,-3)
(-2,-3)(-5,-6)(-4,3)(2
,
3)
(3)分别写出关于二、四象限角平分线的对称点.
课堂练习
1.在平面直角坐标系中,已知点关于x
轴或y
轴的
对称点的坐标有什么变化规律?
2.画一个图形关于x
轴或y
轴对称的图形的方法和步骤.
点(x,y)关于x
轴对称的点的坐标为(
x,-y
);
点(x,y)关于y
轴对称的点的坐标为(
-x,y
).
(1)求特殊点的坐标;(2)描点;(3)连线.
课堂练习
再
见
第十三章
轴对称
13.2
画轴对称图形
第2课时
1
.理解在平面直角坐标系中,已知点关于x轴或y轴对称的点的坐标的变化规律.培语言表达能力、观察能和归纳能力.
2
.掌握在平面直角坐标系中作出一个图形的轴对称图形的方法.加深对轴对称的理解和掌握.
学习目标
情境导入
老北京的地图中,其中西直门和东直门是关于中轴线对称的,如果以天安门为原点,分别以长安
街和中轴线为x轴和y轴建
立平面直角坐标系,对照
东直门的坐标,你能找到
西直门的位置,说出西直
门的坐标吗?
用坐标表示轴对称,可以很方便地确定一个地方的位置,实际上在我们日常生活中应用非常广泛,如工程建设的绘图等.这节课我们就来学习用坐标表示轴对称.
情境导入
x
y
1
1
O
A
B
C
E
D
(1)在直角坐标系中画出下列点A(2,-3),B
(-1,2),C(-6,-5),D(4,0),E(0,-3).
探究新知
(2)画出这些点分别关于x轴、y轴对称的点,并填写表格.
(3)请你仔细观察点的坐标,你能发现关于坐标轴对称的点的坐标有什么规律吗?
(4)请你想办法检验你所发现的规律的正确性,并说说你是如何检验的.
关于x轴、y轴对称的点的坐标规律
在平面直角坐标系中,画出下列已知点关于x
轴对称的点,把它们的坐标填入表格中.
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(4,0)
E(0,-3)
关于x轴的对称点
关于x轴、y轴对称的点的坐标规律
C′
A′
x
y
1
1
O
A
B
C
E
D
D′
B′
E′
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(4,0)
E(0,-3)
关于x轴的对称点
A′(2,3)
B′(-1,-2)
C′(-6,5)
D′(4,0)
E′(0,3)
关于x轴、y轴对称的点的坐标规律
关于x
轴对称的每对对称点的横坐标相等,纵坐标互为相反数.
观察下图中关于x
轴对称的每对对称点的坐标有怎样的变化规律?
C′
A′
x
y
1
1
O
A
B
C
E
D
D′
B′
E′
关于x轴、y轴对称的点的坐标规律
在平面直角坐标系中,画出下列已知点关于y
轴对称的点,把它们的坐标填入表格中.
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(4,0)
E(0,-3)
关于y轴的对称点
关于x轴、y轴对称的点的坐标规律
x
y
1
1
O
A
B
C
E
D
A〞
B〞
C〞
E〞
D〞
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(4,0)
E(0,-3)
关于y轴的对称点
A′′(-2,-3)
B′′(1,2)
C′′(6,-5)
D′′(-4,0)
E′′(0,-3)
关于x轴、y轴对称的点的坐标规律
观察关于y
轴对称的每对对称点的坐标有怎样的变化规律?
关于y
轴对称的每对对称点的横坐标互为相反数,纵坐标相等.
x
y
1
1
O
A
B
C
E
D
A〞
B〞
C〞
E〞
D〞
关于x轴、y轴对称的点的坐标规律
再找几个点,检验一下你发现的规律.
点(x,y)关于x
轴对称的点的坐标为(___,___);
点(x,y)关于y
轴对称的点的坐标为(___,___).
x
-y
-x
y
x
y
1
1
O
x
y
1
1
O
关于x轴、y轴对称的点的坐标规律
【例】如图,四边形ABCD
的四个顶点的坐标分别为
A(-5,1),B(-2,1),
C(-2,5),D(-5,4),
分别画出与四边形ABCD
关
于x
轴和y
轴对称的图形.
x
y
1
1
O
A
B
C
D
例题解析
解:点(x,y)关于y
轴对称的点的坐标为(-x,y),因此四边形ABCD
的顶点A,B,C,D
关于y
轴对称
的点分别为:
A′(
,
),
B′(
,
),
C′(
,
),
D′(
,
),
x
y
1
1
O
A
B
C
D
2
5
5
1
2
1
5
4
A′
B′
C′
D′
例题解析
解:依次连接
,
,
,
,
就可得到与四边形ABCD
关于y轴对称的四边形
.
x
y
1
1
O
A
B
C
D
A′B′C′D′
A′B′
B′C′
C′D′
D′A′
A′
B′
C′
D′
例题解析
解:点(x,y)关于x
轴对称的点的坐标为(-x,y),因此四边形ABCD
的顶点A,B,C,D
关于x
轴对称
的点分别为:
A′′(
,
),
B′′
(
,
),
C′′(
,
),
D′′(
,
),
x
y
1
1
O
A
B
C
D
D′′
C′′
B′′
A′′
-2
-5
-5
-1
-2
-1
-5
-4
例题解析
解:依次连接
,
,
,
,
就可得到与四边形ABCD
关于x轴对称的四边形
.
x
y
1
1
O
A
B
C
D
D′′
C′′
B′′
A′′
A′′B′′C
′′
D
′′
A′′B′′
B′′C′′
C′′D′′
D′′A′′
例题解析
先求出已知图形中一些特殊点(多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
简记为:
(1)求特殊点的坐标;(2)描点;(3)连线.
画一个图形关于x
轴或y
轴对称的图形的方法和步骤.
方法小结
1.分别写出下列各点关于x
轴和y
轴对称的点的坐标:(-2,6),(1,-2),(-1,3),(-4,-2),(1,0)
.
解:关于x
轴对称的点的坐标:(-2,-6),
(1,2),(-1,-3),(-4,2),(1,0).
关于y
轴对称的点的坐标:(2,6),(-1,-2),
(1,3),(4,-2),(-1,0).
课堂练习
2.若点P(2a+b,-3a)与点P′(8,b+2)
关于x
轴对称,则a=
,b=
;
若关于y
轴对称,则a=
,b=_____.
4
-20
2
6
课堂练习
3.以正方形ABCD
的中心为原点建立平面直角坐标系.点A
的坐标为(1,1),写出点B,C,D
的坐标.
A
(1,1)
B
C
D
O
y
x
B(1,-1)
C(-1,-1)
D(-1,1)
课堂练习
4.已知点(3,2)(6,5)(-3,4)(
-3,
-2).
(1)分别写出关于原点对称的点;
(-3,-2)(-6,-5)(3,-4)(3,2)
(2)分别写出关于一、三象限角平分线的
对称点;
(2,3)(5,6)(4,-3)(-2,-3)
(-2,-3)(-5,-6)(-4,3)(2
,
3)
(3)分别写出关于二、四象限角平分线的对称点.
课堂练习
1.在平面直角坐标系中,已知点关于x
轴或y
轴的
对称点的坐标有什么变化规律?
2.画一个图形关于x
轴或y
轴对称的图形的方法和步骤.
点(x,y)关于x
轴对称的点的坐标为(
x,-y
);
点(x,y)关于y
轴对称的点的坐标为(
-x,y
).
(1)求特殊点的坐标;(2)描点;(3)连线.
课堂练习
再
见
