【数学】2-4《向量在平面几何解题中的应用》课件(新人教b版必修4)
文档属性
| 名称 | 【数学】2-4《向量在平面几何解题中的应用》课件(新人教b版必修4) |

|
|
| 格式 | rar | ||
| 文件大小 | 321.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
一、向量有关知识复习
(1)向量共线的充要条件:
与 共线
(2)向量垂直的充要条件:
(3)两向量相等充要条件:
且方向相同。
(4)平面向量基本定理
二、应用向量知识证明平面几何有关定理
例1、证明直径所对的圆周角是直角
A
B
C
O
如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点。求证∠ACB=90°
分析:要证∠ACB=90°,只须证向
量 ,即 。
即 ,∠ACB=90°
思考:能否用向量坐标形式证明?
二、应用向量知识证明平面几何有关定理
例2、证明平行四边形四边平方和等于两对角线平方和
A
B
D
C
已知:平行四边形ABCD。
求证:
解:设 ,则
分析:因为平行四边形对边平行且相
等,故设 其它线段对应向
量用它们表示。
∴
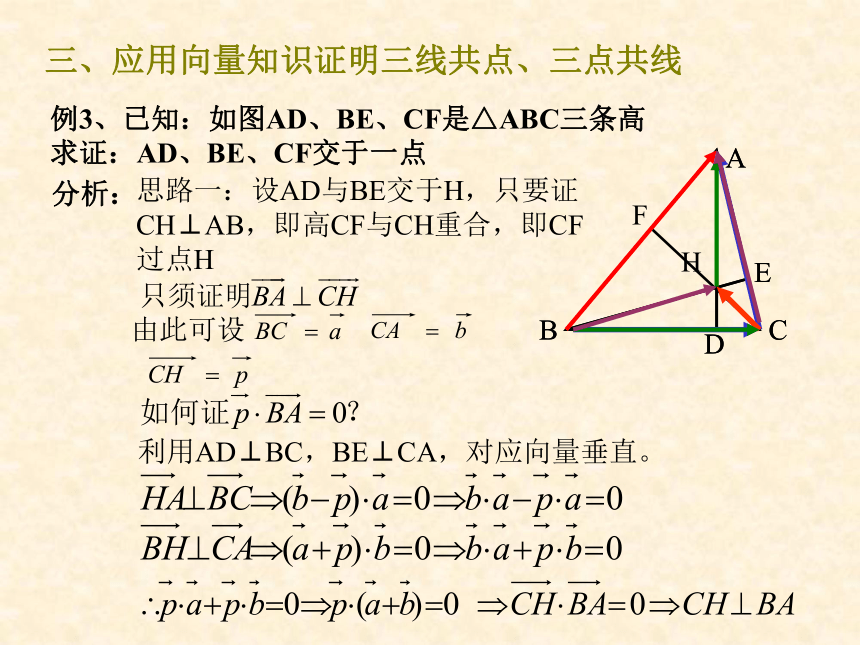
三、应用向量知识证明三线共点、三点共线
例3、已知:如图AD、BE、CF是△ABC三条高
求证:AD、BE、CF交于一点
F
A
B
C
D
E
A
B
C
D
E
H
分析:
思路一:设AD与BE交于H,只要证
CH⊥AB,即高CF与CH重合,即CF
过点H
由此可设
利用AD⊥BC,BE⊥CA,对应向量垂直。
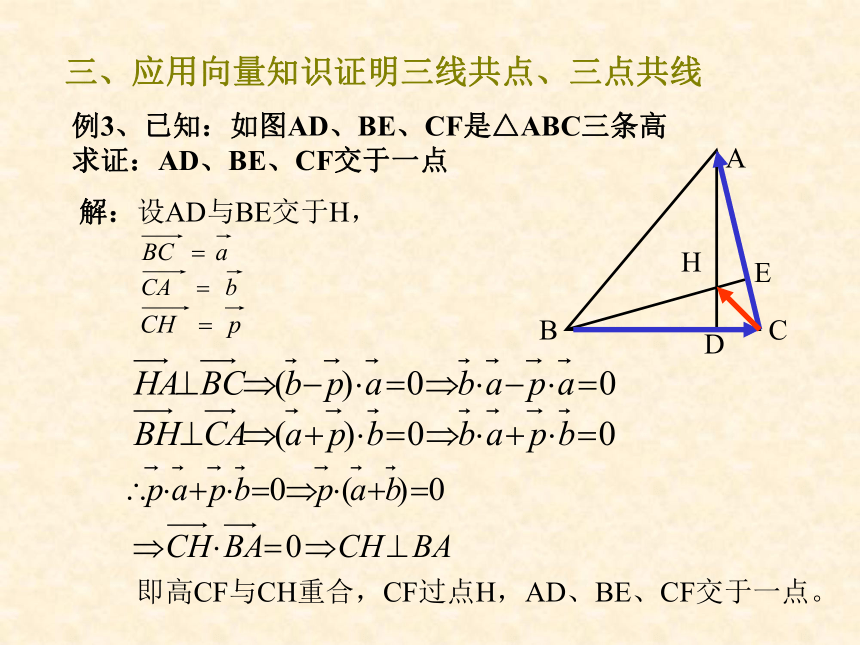
三、应用向量知识证明三线共点、三点共线
例3、已知:如图AD、BE、CF是△ABC三条高
求证:AD、BE、CF交于一点
A
B
C
D
E
H
解:设AD与BE交于H,
即高CF与CH重合,CF过点H,AD、BE、CF交于一点。
三、应用向量知识证明三线共点、三点共线
例4、如图已知△ABC两边AB、AC的中点分别为M、N,
在BN延长线上取点P,使NP=BN,在CM延长线上取点Q,
使MQ=CM。求证:P、A、Q三点共线
A
B
C
N
M
Q
P
解:设
则
由此可得
即 故有 ,且它们有
公共点A,所以P、A、Q三点共线
四、应用向量知识证明等式、求值
例5、如图ABCD是正方形M是BC的中点,将正方形折起,
使点A与M重合,设折痕为EF,若正方形面积为64,
求△AEM的面积
A
B
C
D
M
N
E
F
分析:如图建立坐标系,设E(e,0),M(8,4),
N是AM的中点,故N(4,2)
=(4,2)-(e,0)=(4-e,2)
解得:e=5
故△AEM的面积为10
四、应用向量知识证明等式、求值
例5、如图ABCD是正方形M是BC的中点,将正方形折起,
使点A与M重合,设折痕为EF,若正方形面积为64,
求△AEM的面积
A
B
C
D
M
N
E
F
解:如图建立坐标系,设E(e,0),由
正方形面积为64,可得边长为8
由题意可得M(8,4),N是AM的
中点,故N(4,2)
=(4,2)-(e,0)=(4-e,2)
解得:e=5 即AE=5
四、应用向量知识证明等式、求值
练习:PQ过△OAB的重心G,且OP=mOA,OQ=nOB
求证:
分析:由题意OP=mOA,OQ=nOB,
联想线段的定比分点,利
用向量坐标知识进行求解。
O
A
B
G
·
P
Q
由PO=mOA, QO=nOB可知:
O分 的比为 ,O分 的比为
由此可设 由向量定比分点公式,可求
P、Q的坐标,而G为重心,其坐标也可求出,进而
由向量 ,得到 m n 的关系。
-m -n
四、应用向量知识证明等式、求值
练习:PQ过△OAB的重心G,且OP=mOA,OQ=nOB
求证:
O
A
B
G
·
P
Q
证:如图建立坐标系,
设
所以重心G的坐标为
由PO=mOA, QO=nOB可知:
即O分 的比为-m,O分 的比为-n
求得
由向量 可得:
化简得:
五、小结、巩固练习:
练习1:证明对角线互相垂直平分的四边形是菱形
练习2:如图O为△ABC所在平面内一点,且满足
求证:AB⊥OC
A
B
C
O
一、向量有关知识复习
(1)向量共线的充要条件:
与 共线
(2)向量垂直的充要条件:
(3)两向量相等充要条件:
且方向相同。
(4)平面向量基本定理
二、应用向量知识证明平面几何有关定理
例1、证明直径所对的圆周角是直角
A
B
C
O
如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点。求证∠ACB=90°
分析:要证∠ACB=90°,只须证向
量 ,即 。
即 ,∠ACB=90°
思考:能否用向量坐标形式证明?
二、应用向量知识证明平面几何有关定理
例2、证明平行四边形四边平方和等于两对角线平方和
A
B
D
C
已知:平行四边形ABCD。
求证:
解:设 ,则
分析:因为平行四边形对边平行且相
等,故设 其它线段对应向
量用它们表示。
∴
三、应用向量知识证明三线共点、三点共线
例3、已知:如图AD、BE、CF是△ABC三条高
求证:AD、BE、CF交于一点
F
A
B
C
D
E
A
B
C
D
E
H
分析:
思路一:设AD与BE交于H,只要证
CH⊥AB,即高CF与CH重合,即CF
过点H
由此可设
利用AD⊥BC,BE⊥CA,对应向量垂直。
三、应用向量知识证明三线共点、三点共线
例3、已知:如图AD、BE、CF是△ABC三条高
求证:AD、BE、CF交于一点
A
B
C
D
E
H
解:设AD与BE交于H,
即高CF与CH重合,CF过点H,AD、BE、CF交于一点。
三、应用向量知识证明三线共点、三点共线
例4、如图已知△ABC两边AB、AC的中点分别为M、N,
在BN延长线上取点P,使NP=BN,在CM延长线上取点Q,
使MQ=CM。求证:P、A、Q三点共线
A
B
C
N
M
Q
P
解:设
则
由此可得
即 故有 ,且它们有
公共点A,所以P、A、Q三点共线
四、应用向量知识证明等式、求值
例5、如图ABCD是正方形M是BC的中点,将正方形折起,
使点A与M重合,设折痕为EF,若正方形面积为64,
求△AEM的面积
A
B
C
D
M
N
E
F
分析:如图建立坐标系,设E(e,0),M(8,4),
N是AM的中点,故N(4,2)
=(4,2)-(e,0)=(4-e,2)
解得:e=5
故△AEM的面积为10
四、应用向量知识证明等式、求值
例5、如图ABCD是正方形M是BC的中点,将正方形折起,
使点A与M重合,设折痕为EF,若正方形面积为64,
求△AEM的面积
A
B
C
D
M
N
E
F
解:如图建立坐标系,设E(e,0),由
正方形面积为64,可得边长为8
由题意可得M(8,4),N是AM的
中点,故N(4,2)
=(4,2)-(e,0)=(4-e,2)
解得:e=5 即AE=5
四、应用向量知识证明等式、求值
练习:PQ过△OAB的重心G,且OP=mOA,OQ=nOB
求证:
分析:由题意OP=mOA,OQ=nOB,
联想线段的定比分点,利
用向量坐标知识进行求解。
O
A
B
G
·
P
Q
由PO=mOA, QO=nOB可知:
O分 的比为 ,O分 的比为
由此可设 由向量定比分点公式,可求
P、Q的坐标,而G为重心,其坐标也可求出,进而
由向量 ,得到 m n 的关系。
-m -n
四、应用向量知识证明等式、求值
练习:PQ过△OAB的重心G,且OP=mOA,OQ=nOB
求证:
O
A
B
G
·
P
Q
证:如图建立坐标系,
设
所以重心G的坐标为
由PO=mOA, QO=nOB可知:
即O分 的比为-m,O分 的比为-n
求得
由向量 可得:
化简得:
五、小结、巩固练习:
练习1:证明对角线互相垂直平分的四边形是菱形
练习2:如图O为△ABC所在平面内一点,且满足
求证:AB⊥OC
A
B
C
O
