21.2.1 解一元二次方程--配方法(2)-人教版九年级数学上册(预习 自主)练习
文档属性
| 名称 | 21.2.1 解一元二次方程--配方法(2)-人教版九年级数学上册(预习 自主)练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 51.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
图片预览




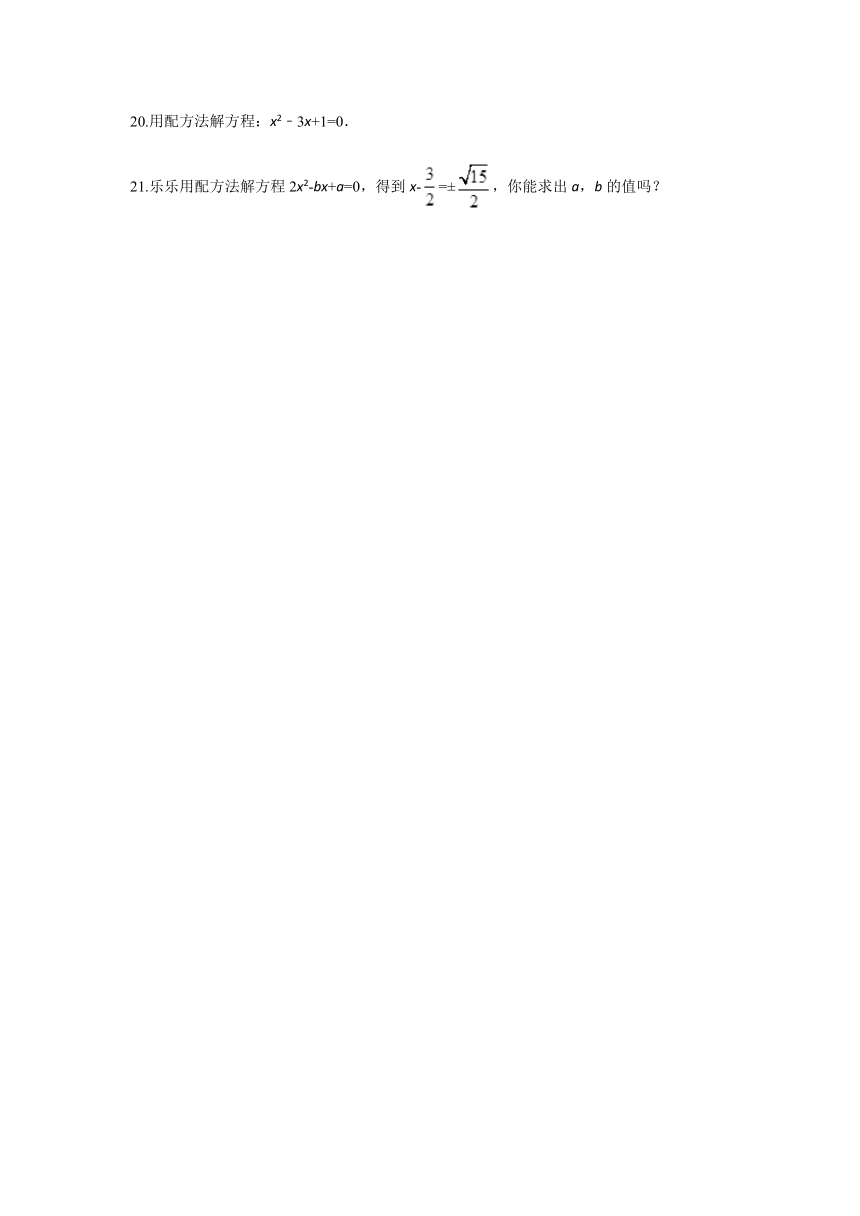
文档简介
21.2.1解一元二次方程---配方法(2)
一、自主预习:
1.
阅读教材P6-9,回答下列问题:
2.将下列各式配成完全平方式:
(1)x2
-12x+_____=(x+_____)2;
(2)x2
–
x
+______=(x-_____)2;
(3)x2
-
x
+_______=(x-____)2
3.回顾:
(1)等式的基本性质是什么?
(2)用直接开平方法解一元二次方程x2
+
6x
+
9
=
7
二、合作探究:
1、解一元二次方程x2+12x=15的困难在哪里?
如何转化才能将其化为上面方程的形式求
解?
试试看.
2、对于一元二次方程x2-2x
-2
=0,如何转化才能化为上面方程的形式求解?
试试看.
3、上面解一元二次方程的方法叫什么方法比较合适?
请你给这种方法下一个定义,并简要说明这种方法的基本思想.
归纳梳理
1.配方法的基本要求是把一元二次方程的一边配方化为一个__________,另一边化为_________________,然后用法求解.
2.配方法的一般步骤:
(1)移项,使方程左边为_________项、_______项,右边为_____项:(一移)
(2)方程两边都除以______系数,将________系数化为l:(二除)
(3)配方,方程两边都加上_________________的平方,使方程左边成为一个__________,右边是一个______________的形式;(三配)
(4)如果右边是___________,两边直接开平方,求这个一元二次方程的解.(四开)
如果右边是负数.则这个方程没有实数解.
三、课后练习:
一.利用配方法进行配方
1.配方:x2-3x+_______=(x-______)2
( )
A.
9,3
B.
3,3
C.,
D.,
2.若把代数式x2-2x+3化为(x-m)2+k形式,其中m,k为常数,结果为( )
A.
(x+1)2+4
B.
(x-1)2+2
C.
(x-1)2+4
D.
(x+1)2+2
3.用配方法将二次三项式x2-6x+5变形的结果是( )
A.
(x-3)2+8
B.
(x+3)2+14
C.
(x-3)2-4
D.
(x-3)2+14
4.将x2+6x+3配方成(x+m)2+n的形式,则m=______.
5.填上适当的数,使等式成立:x2-5x+(_______)2=(x-_______)2;
x2+3x+(______)2=(x+________)2.
6.4x2_________+1=(2x±1)2.
7.填上适当的数,使下列等式成立:y2+_______+()2=(y+___________)2.
8.若ax2+2x+=(2x+)2+m,则a=_______,m=______.
二.用配方法解一元二次方程
1.用配方法解一元二次方程x2+4x-5=0,此方程可变形为( )
A.
(x+2)2=9
B.
(x-2)2=9
C.
(x+2)2=1
D.
(x-2)2=1
2.用配方法解方程2x2-4x+1=0时,配方后所得的方程为( )
A.
(x-2)2=3
B.
2(x-2)2=3
C.
2(x-1)2=1
D.
2(x?1)2=
3.把一元二次方程x2-6x+4=0化成(x+n)2=m的形式时,m+n的值为( )
A.
8
B.
6
C.
3
D.
2
4.把方程x2﹣8x+3=0化成(x+m)2=n的形式,则m,n的值是( )
A.
4,13
B.
﹣4,19
C.
﹣4,13
D.
4,19
5.将一元二次方程式x2﹣6x﹣5=0化成(x+a)2=b的形式,则b=( )
A.
﹣4
B.
4
C.
﹣14
D.
14
6.方程x2+1=2x的根是( )
A.x1=1,x2=-1
B.x1=x2=1
C.x1=x2=-1
D.x1=1+,x2=1-
7.如果一元二次方程x2-ax+6=0经配方后,得(x+3)2=3,则a的值为( )
A.
3
B.
-3
C.
6
D.
-6
8.用配方法解关于x的一元二次方程x2-2x-m=0,配方后得到的方程为( )
A.
(x-1)2=m-1
B.
(x-1)2=m+1
C.
(x-1)2=1-m
D.
(x-1)2=m2-1
9.用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为( )
A.
(x+)2=
B.
(x+)2=
C.
(x-)2=
D.
(x-)2=
10.用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.
2t2﹣7t﹣4=0化为(t﹣)2=
D.
3x2﹣4x﹣2=0化为(x﹣)2=
11.若一元二次方程式4x2+12x-1147=0的两根为a、b,且a>b,则3a+b之值为何?( )
A.
22
B.
28
C.
34
D.
40
12.用配方法解方程2x2-x=4,配方后方程可化为(x-)2=________.
13.一元二次方程x2+3-2x=0的解是_____________.
14.小明设计了一个魔术盒,当任意实数对(a,b)进入其中,会得到一个新的实数a2-2b+3.若将实数(x,-2x)放入其中,得到-1,则x=____________.
15.若代数式x2+9的值与-6x的值相等,则x的值为______
16.若x2-6xy+9y2=0,则=_________.
17.用配方法解方程:x2+5x﹣3=0.
18.用配方法解一元二次方程:3x2﹣6x﹣1=0.
19.用配方法解方程x2﹣4x+1=0.
20.用配方法解方程:x2﹣3x+1=0.
21.乐乐用配方法解方程2x2-bx+a=0,得到x-=±,你能求出a,b的值吗?
答案解析
1.【答案】D
【解析】根据完全平方公式直接配方即可解决问题.
x2?3x+=(x?)2.
2.【答案】B
【解析】x2-2x+3=x2-2x+1+2=(x-1)2+2.
3.【答案】C
【解析】x2-6x+5,
=x2-6x+9-9+5,
=(x2-6x+9)-4,=(x-3)2-4.
4.【答案】3
【解析】x2+6x+3=x2+6x+9-6=(x+3)2-6=(x+m)2+n,则m=3.
5.【答案】-;;;
【解析】根据完全平方公式可知左边加上一次项系数一半的平方即可.
6.【答案】±4x
【解析】4x2±4x+1=(2x±1)2.
7.【答案】±y;±
【解析】y2+(±y)+()2=[y+(±)]2.
8.【答案】4;
【解析】∵ax2+2x+=(2x+)2+m=4x2+2x++m,
∴a=4,m=.
1.【答案】A
【解析】x2+4x-5=0,x2+4x=5,x2+4x+22=5+22,(x+2)2=9,
2.【答案】C
【解析】x2-2x=-,x2-2x+1=-+1,所以(x-1)2=.
3.【答案】D
【解析】x2-6x=-4,x2-6x+9=-4+9,(x-3)2=5,所以n=-3,m=5,所以m+n=5-3=2.
4.【答案】C
【解析】∵x2﹣8x+3=0,
∴x2﹣8x=﹣3,
∴x2﹣8x+16=﹣3+16,
∴(x﹣4)2=13.
∴m=﹣4,n=13.
5.【答案】D
【解析】∵x2﹣6x﹣5=0,∴x2﹣6x=5,
∴x2﹣6x+9=5+9,
∴(x﹣3)2=14.∴b=14.
6.【答案】B
【解析】把方程x2+1=2x移项,得到x2-2x+1=0,∴(x-1)2=0,∴x-1=0,∴x1=x2=1.
7.【答案】D
【解析】由(x+3)2=3,得到x2+6x+9=3,即x2+6x+6=0,∵方程x2-ax+6=0经配方后,得(x+3)2=3,∴x2-ax+6=x2+6x+6,则a=-6.
8.【答案】B
【解析】把方程x2-2x-m=0的常数项移到等号的右边,得到x2-2x=m,方程两边同时加上一次项系数一半的平方,得到x2-2x+1=m+1,配方得(x-1)2=m+1.
9.【答案】A
【解析】ax2+bx+c=0,ax2+bx=-c,x2+x=-,x2+x+()2=-+()2,(x+)2=.
10.【答案】B
【解析】∵x2﹣2x﹣99=0,
∴x2﹣2x=99,
∴x2﹣2x+1=99+1,
∴(x﹣1)2=100,故A选项正确.
∵x2+8x+9=0,∴x2+8x=﹣9,
∴x2+8x+16=﹣9+16,
∴(x+4)2=7,故B选项错误.
∵2t2﹣7t﹣4=0,
∴2t2﹣7t=4,
∴t2﹣t=2,
∴t2﹣t+=2+,
∴(t﹣)2=,故C选项正确.
∵
3x2﹣4x﹣2=0,
∴
3x2﹣4x=2,
∴x2﹣x=,
∴x2﹣x+=+,
∴(x﹣)2=,故D选项正确.
11.【答案】B
【解析】4x2+12x-1147=0,移项得4x2+12x=1147,4x2+12x+9=1147+9,即(2x+3)2=146,2x+3=34,2x+3=-34,解得x=,x=-,∵一元二次方程式4x2+12x-1147=0的两根为a、b,
且a>b,∴a=,b=-,∴3a+b=3×+(-)=28.
12.【答案】
【解析】由原方程,得x2-x=2,配方,得x2-x+()2=2+()2,
即(x-)2=.
13.【答案】x1=x2=
【解析】x2+3-2x=0(x-)2=0∴x1=x2=.
14.【答案】-2
【解析】根据题意得x2-2?(-2x)+3=-1,
整理得x2+4x+4=0,
(x+2)2=0,
所以x1=x2=-2.
15.【答案】-3
【解析】根据题意得x2+9=-6x,整理得x2+6x+9=0,(x+3)2=0,所以x1=x2=-3.
16.【答案】3
【解析】已知等式变形得()2-6?+9=0,
即(-3)2=0,则=3.
17.【答案】解:由原方程移项,得
x2+5x=3,
等式两边同时加上一次项系数一半的平方,得
x2+5x+()2=3+,
∴(x+)2=,
∴x+=±,
解得x=,
∴x1=,x2=.
【解析】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方
18.【答案】解:3x2﹣6x﹣1=0,
方程两边除以3得x2﹣2x﹣=0,
移项得x2﹣2x=,
两边加上1得x2﹣2x+1=,即(x﹣1)2=,
开方得x﹣1=或x﹣1=﹣,
∴方程的解为x1=,x2=.
【解析】将常数项移到等式的右边,含有未知数的项移到等式的左边,然后在等式的两边同时加上一次项系数一半的平方,构成完全平方公式形式;最后直接开平方即可.
19.【答案】解:x2﹣4x=﹣1,
x2﹣4x+4=﹣1+4,
(x﹣2)2=3,
∴x﹣2=,
∴x1=2+,x2=2﹣.
【解析】首先把常数项1移项后,
应该在左右两边同时加上一次项系数﹣4的一半的平方,
然后开方求解即可
20.【答案】解:移项,得x2﹣3x=﹣1,
等式两边同时加上一次项系数一半的平方()2,得
(x-)2=,
x-=±,
∴x1=+,x2=-.
【解析】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
21.【答案】解:∵x-=±,∴2x-3=±,∴(2x-3)2=15,即4x2-12x+9=15,∴2x2-6x-3=0,∴a=-3,b=6.
【解析】把x-=±两边平方,然后整理得到一元二次方程的一般式,从而得到a和b的值.
一、自主预习:
1.
阅读教材P6-9,回答下列问题:
2.将下列各式配成完全平方式:
(1)x2
-12x+_____=(x+_____)2;
(2)x2
–
x
+______=(x-_____)2;
(3)x2
-
x
+_______=(x-____)2
3.回顾:
(1)等式的基本性质是什么?
(2)用直接开平方法解一元二次方程x2
+
6x
+
9
=
7
二、合作探究:
1、解一元二次方程x2+12x=15的困难在哪里?
如何转化才能将其化为上面方程的形式求
解?
试试看.
2、对于一元二次方程x2-2x
-2
=0,如何转化才能化为上面方程的形式求解?
试试看.
3、上面解一元二次方程的方法叫什么方法比较合适?
请你给这种方法下一个定义,并简要说明这种方法的基本思想.
归纳梳理
1.配方法的基本要求是把一元二次方程的一边配方化为一个__________,另一边化为_________________,然后用法求解.
2.配方法的一般步骤:
(1)移项,使方程左边为_________项、_______项,右边为_____项:(一移)
(2)方程两边都除以______系数,将________系数化为l:(二除)
(3)配方,方程两边都加上_________________的平方,使方程左边成为一个__________,右边是一个______________的形式;(三配)
(4)如果右边是___________,两边直接开平方,求这个一元二次方程的解.(四开)
如果右边是负数.则这个方程没有实数解.
三、课后练习:
一.利用配方法进行配方
1.配方:x2-3x+_______=(x-______)2
( )
A.
9,3
B.
3,3
C.,
D.,
2.若把代数式x2-2x+3化为(x-m)2+k形式,其中m,k为常数,结果为( )
A.
(x+1)2+4
B.
(x-1)2+2
C.
(x-1)2+4
D.
(x+1)2+2
3.用配方法将二次三项式x2-6x+5变形的结果是( )
A.
(x-3)2+8
B.
(x+3)2+14
C.
(x-3)2-4
D.
(x-3)2+14
4.将x2+6x+3配方成(x+m)2+n的形式,则m=______.
5.填上适当的数,使等式成立:x2-5x+(_______)2=(x-_______)2;
x2+3x+(______)2=(x+________)2.
6.4x2_________+1=(2x±1)2.
7.填上适当的数,使下列等式成立:y2+_______+()2=(y+___________)2.
8.若ax2+2x+=(2x+)2+m,则a=_______,m=______.
二.用配方法解一元二次方程
1.用配方法解一元二次方程x2+4x-5=0,此方程可变形为( )
A.
(x+2)2=9
B.
(x-2)2=9
C.
(x+2)2=1
D.
(x-2)2=1
2.用配方法解方程2x2-4x+1=0时,配方后所得的方程为( )
A.
(x-2)2=3
B.
2(x-2)2=3
C.
2(x-1)2=1
D.
2(x?1)2=
3.把一元二次方程x2-6x+4=0化成(x+n)2=m的形式时,m+n的值为( )
A.
8
B.
6
C.
3
D.
2
4.把方程x2﹣8x+3=0化成(x+m)2=n的形式,则m,n的值是( )
A.
4,13
B.
﹣4,19
C.
﹣4,13
D.
4,19
5.将一元二次方程式x2﹣6x﹣5=0化成(x+a)2=b的形式,则b=( )
A.
﹣4
B.
4
C.
﹣14
D.
14
6.方程x2+1=2x的根是( )
A.x1=1,x2=-1
B.x1=x2=1
C.x1=x2=-1
D.x1=1+,x2=1-
7.如果一元二次方程x2-ax+6=0经配方后,得(x+3)2=3,则a的值为( )
A.
3
B.
-3
C.
6
D.
-6
8.用配方法解关于x的一元二次方程x2-2x-m=0,配方后得到的方程为( )
A.
(x-1)2=m-1
B.
(x-1)2=m+1
C.
(x-1)2=1-m
D.
(x-1)2=m2-1
9.用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为( )
A.
(x+)2=
B.
(x+)2=
C.
(x-)2=
D.
(x-)2=
10.用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.
2t2﹣7t﹣4=0化为(t﹣)2=
D.
3x2﹣4x﹣2=0化为(x﹣)2=
11.若一元二次方程式4x2+12x-1147=0的两根为a、b,且a>b,则3a+b之值为何?( )
A.
22
B.
28
C.
34
D.
40
12.用配方法解方程2x2-x=4,配方后方程可化为(x-)2=________.
13.一元二次方程x2+3-2x=0的解是_____________.
14.小明设计了一个魔术盒,当任意实数对(a,b)进入其中,会得到一个新的实数a2-2b+3.若将实数(x,-2x)放入其中,得到-1,则x=____________.
15.若代数式x2+9的值与-6x的值相等,则x的值为______
16.若x2-6xy+9y2=0,则=_________.
17.用配方法解方程:x2+5x﹣3=0.
18.用配方法解一元二次方程:3x2﹣6x﹣1=0.
19.用配方法解方程x2﹣4x+1=0.
20.用配方法解方程:x2﹣3x+1=0.
21.乐乐用配方法解方程2x2-bx+a=0,得到x-=±,你能求出a,b的值吗?
答案解析
1.【答案】D
【解析】根据完全平方公式直接配方即可解决问题.
x2?3x+=(x?)2.
2.【答案】B
【解析】x2-2x+3=x2-2x+1+2=(x-1)2+2.
3.【答案】C
【解析】x2-6x+5,
=x2-6x+9-9+5,
=(x2-6x+9)-4,=(x-3)2-4.
4.【答案】3
【解析】x2+6x+3=x2+6x+9-6=(x+3)2-6=(x+m)2+n,则m=3.
5.【答案】-;;;
【解析】根据完全平方公式可知左边加上一次项系数一半的平方即可.
6.【答案】±4x
【解析】4x2±4x+1=(2x±1)2.
7.【答案】±y;±
【解析】y2+(±y)+()2=[y+(±)]2.
8.【答案】4;
【解析】∵ax2+2x+=(2x+)2+m=4x2+2x++m,
∴a=4,m=.
1.【答案】A
【解析】x2+4x-5=0,x2+4x=5,x2+4x+22=5+22,(x+2)2=9,
2.【答案】C
【解析】x2-2x=-,x2-2x+1=-+1,所以(x-1)2=.
3.【答案】D
【解析】x2-6x=-4,x2-6x+9=-4+9,(x-3)2=5,所以n=-3,m=5,所以m+n=5-3=2.
4.【答案】C
【解析】∵x2﹣8x+3=0,
∴x2﹣8x=﹣3,
∴x2﹣8x+16=﹣3+16,
∴(x﹣4)2=13.
∴m=﹣4,n=13.
5.【答案】D
【解析】∵x2﹣6x﹣5=0,∴x2﹣6x=5,
∴x2﹣6x+9=5+9,
∴(x﹣3)2=14.∴b=14.
6.【答案】B
【解析】把方程x2+1=2x移项,得到x2-2x+1=0,∴(x-1)2=0,∴x-1=0,∴x1=x2=1.
7.【答案】D
【解析】由(x+3)2=3,得到x2+6x+9=3,即x2+6x+6=0,∵方程x2-ax+6=0经配方后,得(x+3)2=3,∴x2-ax+6=x2+6x+6,则a=-6.
8.【答案】B
【解析】把方程x2-2x-m=0的常数项移到等号的右边,得到x2-2x=m,方程两边同时加上一次项系数一半的平方,得到x2-2x+1=m+1,配方得(x-1)2=m+1.
9.【答案】A
【解析】ax2+bx+c=0,ax2+bx=-c,x2+x=-,x2+x+()2=-+()2,(x+)2=.
10.【答案】B
【解析】∵x2﹣2x﹣99=0,
∴x2﹣2x=99,
∴x2﹣2x+1=99+1,
∴(x﹣1)2=100,故A选项正确.
∵x2+8x+9=0,∴x2+8x=﹣9,
∴x2+8x+16=﹣9+16,
∴(x+4)2=7,故B选项错误.
∵2t2﹣7t﹣4=0,
∴2t2﹣7t=4,
∴t2﹣t=2,
∴t2﹣t+=2+,
∴(t﹣)2=,故C选项正确.
∵
3x2﹣4x﹣2=0,
∴
3x2﹣4x=2,
∴x2﹣x=,
∴x2﹣x+=+,
∴(x﹣)2=,故D选项正确.
11.【答案】B
【解析】4x2+12x-1147=0,移项得4x2+12x=1147,4x2+12x+9=1147+9,即(2x+3)2=146,2x+3=34,2x+3=-34,解得x=,x=-,∵一元二次方程式4x2+12x-1147=0的两根为a、b,
且a>b,∴a=,b=-,∴3a+b=3×+(-)=28.
12.【答案】
【解析】由原方程,得x2-x=2,配方,得x2-x+()2=2+()2,
即(x-)2=.
13.【答案】x1=x2=
【解析】x2+3-2x=0(x-)2=0∴x1=x2=.
14.【答案】-2
【解析】根据题意得x2-2?(-2x)+3=-1,
整理得x2+4x+4=0,
(x+2)2=0,
所以x1=x2=-2.
15.【答案】-3
【解析】根据题意得x2+9=-6x,整理得x2+6x+9=0,(x+3)2=0,所以x1=x2=-3.
16.【答案】3
【解析】已知等式变形得()2-6?+9=0,
即(-3)2=0,则=3.
17.【答案】解:由原方程移项,得
x2+5x=3,
等式两边同时加上一次项系数一半的平方,得
x2+5x+()2=3+,
∴(x+)2=,
∴x+=±,
解得x=,
∴x1=,x2=.
【解析】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方
18.【答案】解:3x2﹣6x﹣1=0,
方程两边除以3得x2﹣2x﹣=0,
移项得x2﹣2x=,
两边加上1得x2﹣2x+1=,即(x﹣1)2=,
开方得x﹣1=或x﹣1=﹣,
∴方程的解为x1=,x2=.
【解析】将常数项移到等式的右边,含有未知数的项移到等式的左边,然后在等式的两边同时加上一次项系数一半的平方,构成完全平方公式形式;最后直接开平方即可.
19.【答案】解:x2﹣4x=﹣1,
x2﹣4x+4=﹣1+4,
(x﹣2)2=3,
∴x﹣2=,
∴x1=2+,x2=2﹣.
【解析】首先把常数项1移项后,
应该在左右两边同时加上一次项系数﹣4的一半的平方,
然后开方求解即可
20.【答案】解:移项,得x2﹣3x=﹣1,
等式两边同时加上一次项系数一半的平方()2,得
(x-)2=,
x-=±,
∴x1=+,x2=-.
【解析】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
21.【答案】解:∵x-=±,∴2x-3=±,∴(2x-3)2=15,即4x2-12x+9=15,∴2x2-6x-3=0,∴a=-3,b=6.
【解析】把x-=±两边平方,然后整理得到一元二次方程的一般式,从而得到a和b的值.
同课章节目录
