2020-2021学年人教版八年级数学上册 第12.2 全等三角形的判定 暑假提高训练(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学上册 第12.2 全等三角形的判定 暑假提高训练(word版含答案) | 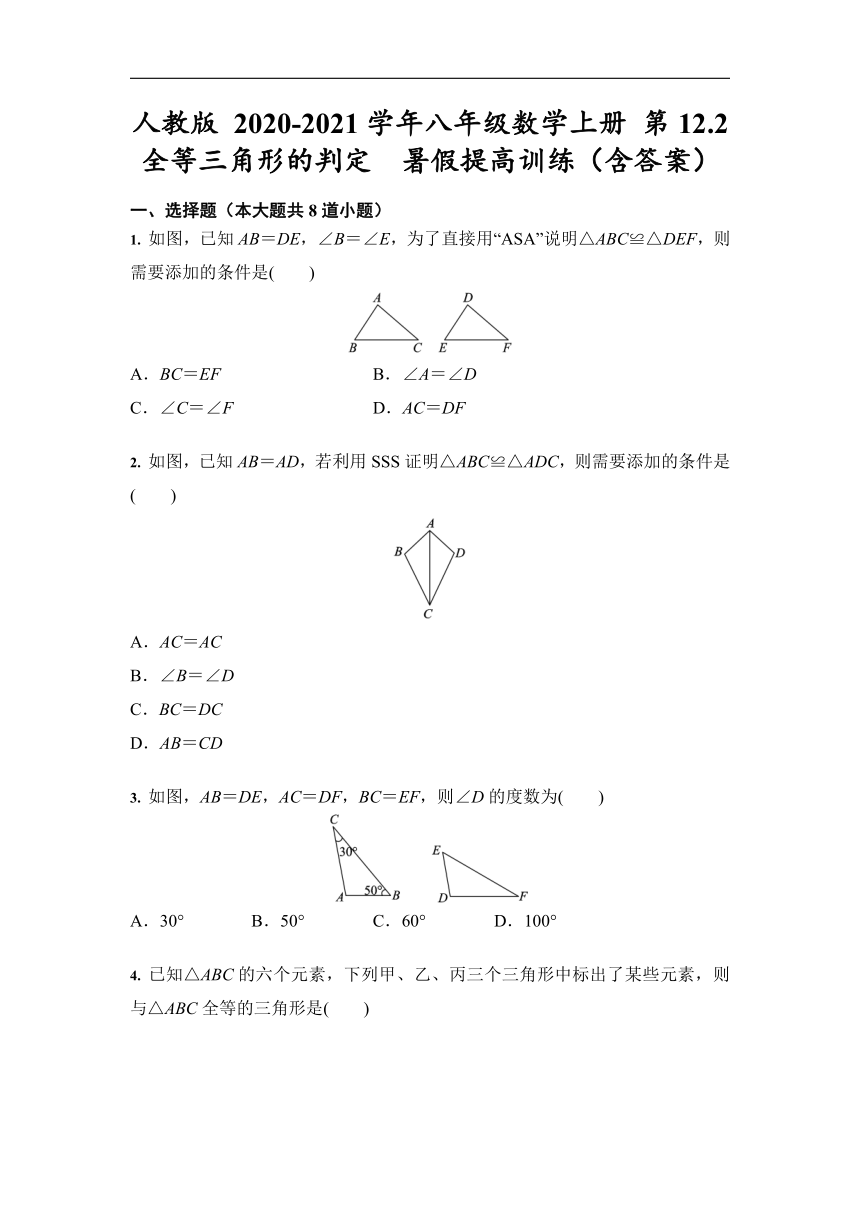 | |
| 格式 | zip | ||
| 文件大小 | 390.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 08:57:47 | ||
图片预览


文档简介
人教版
2020-2021学年八年级数学上册
第12.2
全等三角形的判定
暑假提高训练(含答案)
一、选择题(本大题共8道小题)
1.
如图,已知AB=DE,∠B=∠E,为了直接用“ASA”说明△ABC≌△DEF,则需要添加的条件是( )
A.BC=EF
B.∠A=∠D
C.∠C=∠F
D.AC=DF
2.
如图,已知AB=AD,若利用SSS证明△ABC≌△ADC,则需要添加的条件是( )
A.AC=AC
B.∠B=∠D
C.BC=DC
D.AB=CD
3.
如图,AB=DE,AC=DF,BC=EF,则∠D的度数为( )
A.30°
B.50°
C.60°
D.100°
4.
已知△ABC的六个元素,下列甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙
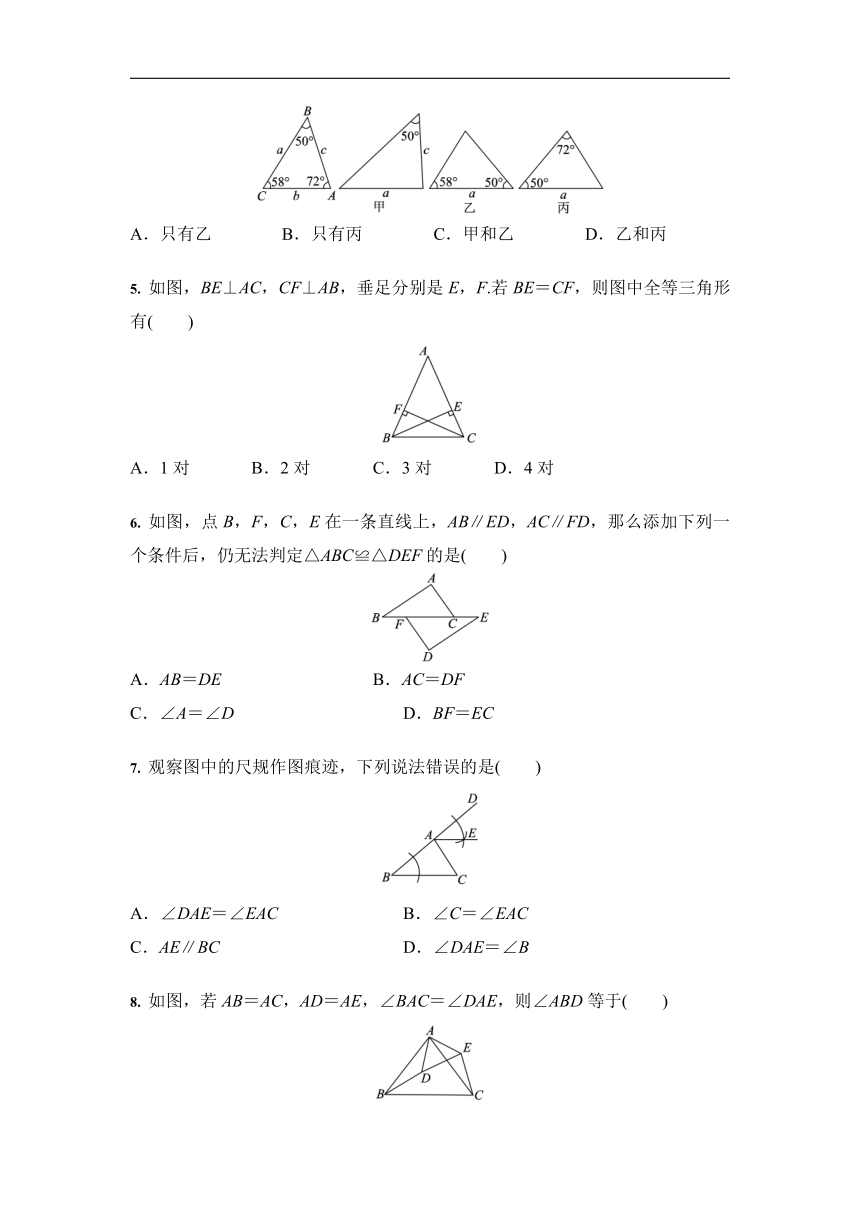
5.
如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对
B.2对
C.3对
D.4对
6.
如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
7.
观察图中的尺规作图痕迹,下列说法错误的是( )
A.∠DAE=∠EAC
B.∠C=∠EAC
C.AE∥BC
D.∠DAE=∠B
8.
如图,若AB=AC,AD=AE,∠BAC=∠DAE,则∠ABD等于( )
A.∠EAC
B.∠ADE
C.∠BAD
D.∠ACE
二、填空题(本大题共5道小题)
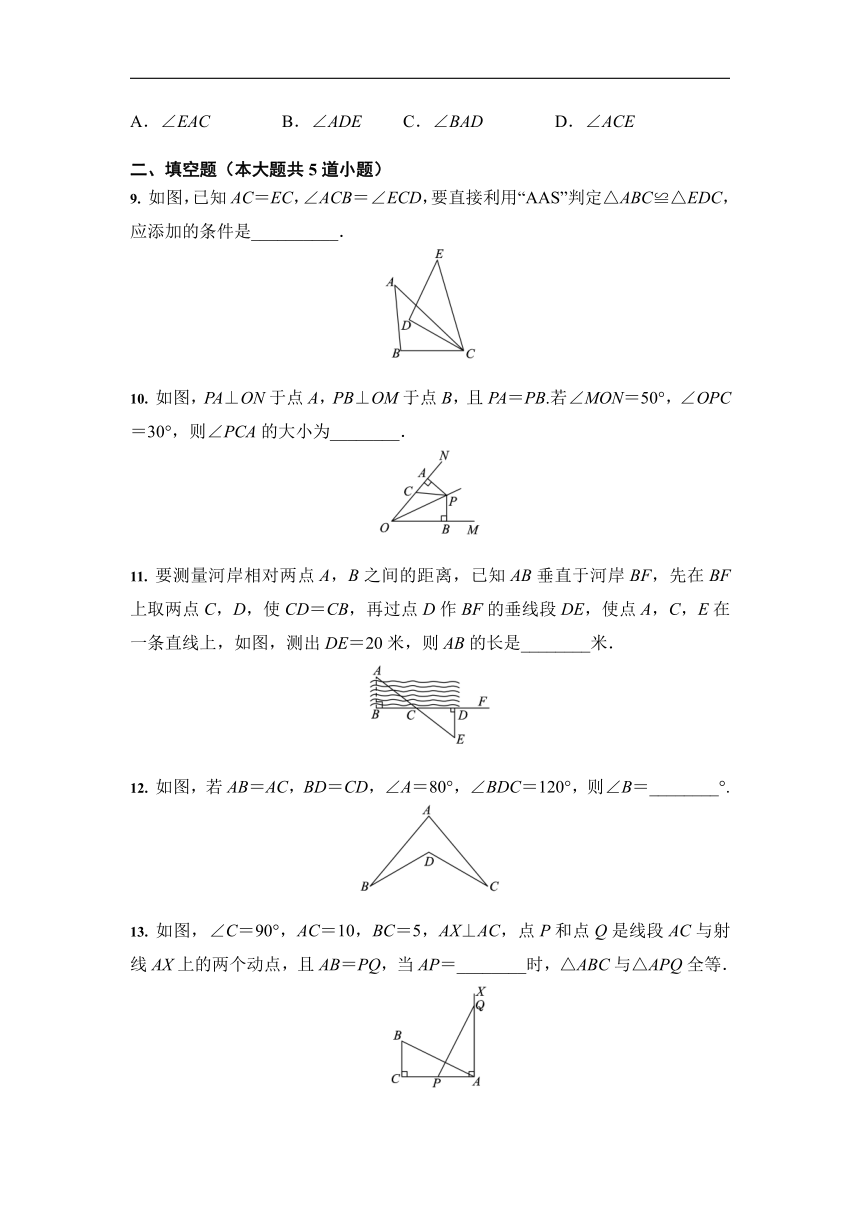
9.
如图,已知AC=EC,∠ACB=∠ECD,要直接利用“AAS”判定△ABC≌△EDC,应添加的条件是__________.
10.
如图,PA⊥ON于点A,PB⊥OM于点B,且PA=PB.若∠MON=50°,∠OPC=30°,则∠PCA的大小为________.
11.
要测量河岸相对两点A,B之间的距离,已知AB垂直于河岸BF,先在BF上取两点C,D,使CD=CB,再过点D作BF的垂线段DE,使点A,C,E在一条直线上,如图,测出DE=20米,则AB的长是________米.
12.
如图,若AB=AC,BD=CD,∠A=80°,∠BDC=120°,则∠B=________°.
13.
如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q是线段AC与射线AX上的两个动点,且AB=PQ,当AP=________时,△ABC与△APQ全等.
三、解答题(本大题共3道小题)
14.
如图,AB=AD,AC=AE,∠BAG=∠DAF.
求证:BC=DE.
15.
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
16.
如图,已知AP∥BC,∠PAB的平分线与∠CBA的平分线相交于点E,过点E的直线分别交AP,BC于点D,C.求证:AD+BC=AB.
人教版
2020-2021学年八年级数学上册
第12.2
全等三角形的判定
暑假提高训练-答案
一、选择题(本大题共8道小题)
1.
【答案】B
2.
【答案】C
3.
【答案】D [解析]
在△ABC和△DEF中,
∴△ABC≌△DEF.∴∠A=∠D.
∵∠A=180°-∠B-∠C=100°,∴∠D=100°.
4.
【答案】D
5.
【答案】C [解析]
①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
6.
【答案】C [解析]
选项A中添加AB=DE可用“AAS”进行判定,故本选项不符合题意;
选项B中添加AC=DF可用“AAS”进行判定,故本选项不符合题意;
选项C中添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;
选项D中添加BF=EC可得出BC=EF,然后可用“ASA”进行判定,故本选项不符合题意.
故选C.
7.
【答案】A [解析]
根据图中尺规作图的痕迹,可得∠DAE=∠B,故D选项正确,∴AE∥BC,故C选项正确.∴∠EAC=∠C,故B选项正确.
∵∠DAE=∠B,∠EAC=∠C,而∠C与∠B的大小关系不确定,所以∠DAE与∠EAC的大小关系不确定.故选A.
8.
【答案】D [解析]
∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE.
二、填空题(本大题共5道小题)
9.
【答案】∠B=∠D
10.
【答案】55° [解析]
∵PA⊥ON,PB⊥OM,
∴∠PAO=∠PBO=90°.
在Rt△AOP和Rt△BOP中,
∴Rt△AOP≌Rt△BOP(HL).
∴∠AOP=∠BOP=∠MON=25°.
∴∠PCA=∠AOP+∠OPC=25°+30°=55°.
11.
【答案】20
12.
【答案】20 [解析]
如图,过点D作射线AF.
在△BAD和△CAD中,
∴△BAD≌△CAD(SSS).
∴∠BAD=∠CAD,∠B=∠C.
∵∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠BAD+∠C+∠CAD,
即∠BDC=∠B+∠C+∠BAC.
∵∠BAC=80°,∠BDC=120°,
∴∠B=∠C=20°.
13.
【答案】5或10 [解析]
∵AX⊥AC,∴∠PAQ=90°.∴∠C=∠PAQ=90°.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在Rt△ABC和Rt△PQA中,
∴Rt△ABC≌Rt△PQA(HL).
综上所述,当AP=5或10时,△ABC与△APQ全等.
三、解答题(本大题共3道小题)
14.
【答案】
证明:∵∠BAG=∠DAF,
∴∠BAG+∠CAE=∠DAF+∠CAE,
即∠CAB=∠EAD.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
∴BC=DE.
15.
【答案】
(1)证明:∵BF=EC,
∴BF+FC=EC+CF,即BC=EF.(3分)
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS).(5分)
(2)解:AB∥DE,AC∥DF.(7分)
理由如下:
∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF.(9分)
16.
【答案】
证明:如图,在AB上截取AF=AD,连接EF.
∵AE平分∠PAB,
∴∠DAE=∠FAE.
在△DAE和△FAE中,
∴△DAE≌△FAE(SAS).
∴∠AFE=∠ADE.
∵AD∥BC,
∴∠ADE+∠C=180°.
又∵∠AFE+∠EFB=180°,
∴∠EFB=∠C.
∵BE平分∠ABC,
∴∠EBF=∠EBC.
在△BEF和△BEC中,
∴△BEF≌△BEC(AAS).
∴BF=BC.
∴AD+BC=AF+BF=AB.
2020-2021学年八年级数学上册
第12.2
全等三角形的判定
暑假提高训练(含答案)
一、选择题(本大题共8道小题)
1.
如图,已知AB=DE,∠B=∠E,为了直接用“ASA”说明△ABC≌△DEF,则需要添加的条件是( )
A.BC=EF
B.∠A=∠D
C.∠C=∠F
D.AC=DF
2.
如图,已知AB=AD,若利用SSS证明△ABC≌△ADC,则需要添加的条件是( )
A.AC=AC
B.∠B=∠D
C.BC=DC
D.AB=CD
3.
如图,AB=DE,AC=DF,BC=EF,则∠D的度数为( )
A.30°
B.50°
C.60°
D.100°
4.
已知△ABC的六个元素,下列甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙
5.
如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对
B.2对
C.3对
D.4对
6.
如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
7.
观察图中的尺规作图痕迹,下列说法错误的是( )
A.∠DAE=∠EAC
B.∠C=∠EAC
C.AE∥BC
D.∠DAE=∠B
8.
如图,若AB=AC,AD=AE,∠BAC=∠DAE,则∠ABD等于( )
A.∠EAC
B.∠ADE
C.∠BAD
D.∠ACE
二、填空题(本大题共5道小题)
9.
如图,已知AC=EC,∠ACB=∠ECD,要直接利用“AAS”判定△ABC≌△EDC,应添加的条件是__________.
10.
如图,PA⊥ON于点A,PB⊥OM于点B,且PA=PB.若∠MON=50°,∠OPC=30°,则∠PCA的大小为________.
11.
要测量河岸相对两点A,B之间的距离,已知AB垂直于河岸BF,先在BF上取两点C,D,使CD=CB,再过点D作BF的垂线段DE,使点A,C,E在一条直线上,如图,测出DE=20米,则AB的长是________米.
12.
如图,若AB=AC,BD=CD,∠A=80°,∠BDC=120°,则∠B=________°.
13.
如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q是线段AC与射线AX上的两个动点,且AB=PQ,当AP=________时,△ABC与△APQ全等.
三、解答题(本大题共3道小题)
14.
如图,AB=AD,AC=AE,∠BAG=∠DAF.
求证:BC=DE.
15.
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
16.
如图,已知AP∥BC,∠PAB的平分线与∠CBA的平分线相交于点E,过点E的直线分别交AP,BC于点D,C.求证:AD+BC=AB.
人教版
2020-2021学年八年级数学上册
第12.2
全等三角形的判定
暑假提高训练-答案
一、选择题(本大题共8道小题)
1.
【答案】B
2.
【答案】C
3.
【答案】D [解析]
在△ABC和△DEF中,
∴△ABC≌△DEF.∴∠A=∠D.
∵∠A=180°-∠B-∠C=100°,∴∠D=100°.
4.
【答案】D
5.
【答案】C [解析]
①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
6.
【答案】C [解析]
选项A中添加AB=DE可用“AAS”进行判定,故本选项不符合题意;
选项B中添加AC=DF可用“AAS”进行判定,故本选项不符合题意;
选项C中添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;
选项D中添加BF=EC可得出BC=EF,然后可用“ASA”进行判定,故本选项不符合题意.
故选C.
7.
【答案】A [解析]
根据图中尺规作图的痕迹,可得∠DAE=∠B,故D选项正确,∴AE∥BC,故C选项正确.∴∠EAC=∠C,故B选项正确.
∵∠DAE=∠B,∠EAC=∠C,而∠C与∠B的大小关系不确定,所以∠DAE与∠EAC的大小关系不确定.故选A.
8.
【答案】D [解析]
∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴∠ABD=∠ACE.
二、填空题(本大题共5道小题)
9.
【答案】∠B=∠D
10.
【答案】55° [解析]
∵PA⊥ON,PB⊥OM,
∴∠PAO=∠PBO=90°.
在Rt△AOP和Rt△BOP中,
∴Rt△AOP≌Rt△BOP(HL).
∴∠AOP=∠BOP=∠MON=25°.
∴∠PCA=∠AOP+∠OPC=25°+30°=55°.
11.
【答案】20
12.
【答案】20 [解析]
如图,过点D作射线AF.
在△BAD和△CAD中,
∴△BAD≌△CAD(SSS).
∴∠BAD=∠CAD,∠B=∠C.
∵∠BDF=∠B+∠BAD,∠CDF=∠C+∠CAD,
∴∠BDF+∠CDF=∠B+∠BAD+∠C+∠CAD,
即∠BDC=∠B+∠C+∠BAC.
∵∠BAC=80°,∠BDC=120°,
∴∠B=∠C=20°.
13.
【答案】5或10 [解析]
∵AX⊥AC,∴∠PAQ=90°.∴∠C=∠PAQ=90°.
分两种情况:①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在Rt△ABC和Rt△PQA中,
∴Rt△ABC≌Rt△PQA(HL).
综上所述,当AP=5或10时,△ABC与△APQ全等.
三、解答题(本大题共3道小题)
14.
【答案】
证明:∵∠BAG=∠DAF,
∴∠BAG+∠CAE=∠DAF+∠CAE,
即∠CAB=∠EAD.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
∴BC=DE.
15.
【答案】
(1)证明:∵BF=EC,
∴BF+FC=EC+CF,即BC=EF.(3分)
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS).(5分)
(2)解:AB∥DE,AC∥DF.(7分)
理由如下:
∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF.(9分)
16.
【答案】
证明:如图,在AB上截取AF=AD,连接EF.
∵AE平分∠PAB,
∴∠DAE=∠FAE.
在△DAE和△FAE中,
∴△DAE≌△FAE(SAS).
∴∠AFE=∠ADE.
∵AD∥BC,
∴∠ADE+∠C=180°.
又∵∠AFE+∠EFB=180°,
∴∠EFB=∠C.
∵BE平分∠ABC,
∴∠EBF=∠EBC.
在△BEF和△BEC中,
∴△BEF≌△BEC(AAS).
∴BF=BC.
∴AD+BC=AF+BF=AB.
