北师版八年级数学上册 1.1.1 勾股定理 能力提升卷(Word版 有答案)
文档属性
| 名称 | 北师版八年级数学上册 1.1.1 勾股定理 能力提升卷(Word版 有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 394.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 06:56:04 | ||
图片预览



文档简介
北师版八年级数学上册
1.1.1勾股定理
能力提升卷
一、选择题(共10小题,3
10=30)
1.直角三角形的两直角边长分别为5,12,则斜边上的高为(
)
A.6
B.8
C. D.
2.在Rt△ABC中,斜边长BC=3,则AB2+AC2+BC2的值为( )
A.18
B.9
C.6
D.无法计算
3.如图,在△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5
B.6
C.8
D.10
4.如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
A.5个
B.4个
C.3个
D.2个
5.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48
B.60
C.76
D.80
6.
如图,在Rt△ABC中,∠ACB=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
A.225
B.200
C.250
D.150
7.
如图,在Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,两个半圆形的面积分别记为S1,S2,则S1+S2的值等于( )
A.2π
B.4π
C.8π
D.16π
8.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载,如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图②的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
9.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方3
km处,过了20
s,飞机距离这个男孩头顶5
km(如图).这一过程中飞机飞行的速度是每秒________千米( )
A.0.2
B.2
C.0.4
D.4
10.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的面积分别为2,5,1,2,则最大的正方形E的面积是( )
A.6
B.8
C.9
D.10
二.填空题(共8小题,3
8=24)
11.无盖圆柱形杯子的展开图如图所示.将一根长为20
cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有________cm.
12.
在△ABC中,∠C=90°,一条直角边长为4
cm,斜边长比另一条直角边长长1
cm,则△ABC的周长是________.
13.在Rt△ABC中,斜边长BC=3,AB2+AC2+BC2的值为________.
14.在△ABC中,若∠B=90°,∠A,∠B,∠C的对边分别是a,b,c,且a=7,b=25,则c的长为________.
15.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是________.
16.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为________.
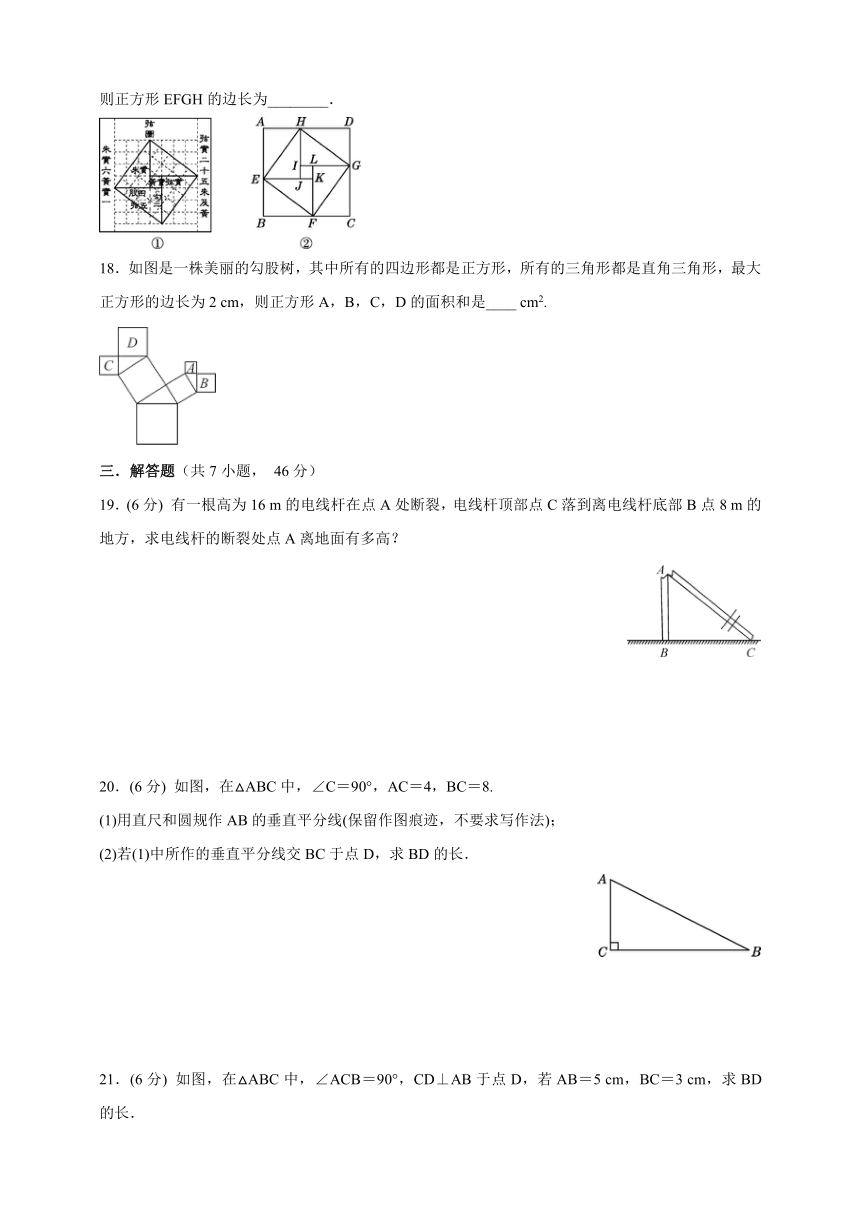
17.我国三国时期的数学家赵爽为了验证勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图①所示.在图②中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,
则正方形EFGH的边长为________.
18.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,最大正方形的边长为2
cm,则正方形A,B,C,D的面积和是____
cm2.
三.解答题(共7小题,
46分)
19.(6分)
有一根高为16
m的电线杆在点A处断裂,电线杆顶部点C落到离电线杆底部B点8
m的地方,求电线杆的断裂处点A离地面有多高?
20.(6分)
如图,在△ABC中,∠C=90°,AC=4,BC=8.
(1)用直尺和圆规作AB的垂直平分线(保留作图痕迹,不要求写作法);
(2)若(1)中所作的垂直平分线交BC于点D,求BD的长.
21.(6分)
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AB=5
cm,BC=3
cm,求BD的长.
22.(6分)
用如图①的四个形状、大小完全一样的直角三角形拼一拼,摆一摆,可以摆成如图②的正方形.请你用这个图形验证勾股定理.
图①
图②
23.(6分)
在一棵树的10
m高处有两只猴子,其中一只爬下树走向离树20
m的池塘,而另一只爬向树顶后直扑池塘(运动路线看作直线),如果两只猴子经过的距离相等,问这棵树有多高?
24.(8分)
如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
25.(8分)
.如图,将长方形纸片ABCD的一边AD向下折叠,点D落在BC边的点F处.已知AB=8
cm,BC=10
cm,求EC的长.
参考答案
1-5DACCC
6-10AACAD
11.
5
12.
20cm
13.
18
14.
24
15.
4
16.
17.
10
18.
4
19.
解:设AB长为x
m,
则有x2+82=(16-x)2,
解得x=6,
故断裂处点A离地面有6
m
20.
解:(1)所作AB的垂直平分线如图所示.
(2)如图,连接AD,由作图可知AD=BD,设BD=x,
则AD=x,CD=8-x.因为∠C=90°,
所以由勾股定理可得AC2+CD2=AD2.
因为AC=4,所以42+(8-x)2=x2,解得x=5.
所以BD=5.
21.
解:由勾股定理可以得到AB2=AC2+BC2,∴AC=4,
由S△ABC=AC·BC=AB·CD,
即×4×3=×5×CD,∴CD=,
∴BD2=BC2-CD2=,
∴BD=(cm)
22.
证明:因为图②中大正方形的面积可以表示为c2+4×ab,也可以表示为(a+b)2,
所以c2+4×ab=(a+b)2.
整理,得c2+2ab=a2+2ab+b2.
即a2+b2=c2.
23.
解:如图,点B为树顶,D处有两只猴子,则AD=10
m,C为池塘,则AC=20
m.
设BD的长为x
m,则树的高度为(10+x)m.
∵AC+AD=BD+BC,∴BC=20+10-x=30-x.
在△ACB中,∠A=90°,∴AC2+AB2=BC2,
即202+(10+x)2=(30-x)2,
解得x=5.
即树高为15
m
24.
解:在△ABC中,作AD⊥BC于点D,设BD=x,则CD=14-x.
由勾股定理,得AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
所以152-x2=132-(14-x)2.
解得x=9.
在Rt△ABD中,AD2=AB2-BD2=152-92=144,
所以AD=12.
所以S△ABC=BC·AD=×14×12=84.
25.
解:根据题意,得△AFE≌△ADE,
所以AF=AD=BC=10
cm,EF=ED.
所以EF+EC=DC=AB=8
cm.
在Rt△ABF中,根据勾股定理得BF2=AF2-AB2=102-82=36,
所以BF=6
cm.所以FC=BC-BF=10-6=4(cm).
设EC=x
cm,则EF=DC-EC=(8-x)
cm.
在Rt△EFC中,根据勾股定理得EC2+FC2=EF2,
即x2+42=(8-x)2.解这个方程,得x=3,即EC的长为3
cm.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
1.1.1勾股定理
能力提升卷
一、选择题(共10小题,3
10=30)
1.直角三角形的两直角边长分别为5,12,则斜边上的高为(
)
A.6
B.8
C. D.
2.在Rt△ABC中,斜边长BC=3,则AB2+AC2+BC2的值为( )
A.18
B.9
C.6
D.无法计算
3.如图,在△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5
B.6
C.8
D.10
4.如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
A.5个
B.4个
C.3个
D.2个
5.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48
B.60
C.76
D.80
6.
如图,在Rt△ABC中,∠ACB=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
A.225
B.200
C.250
D.150
7.
如图,在Rt△ABC中,AB=4,分别以AC,BC为直径作半圆,两个半圆形的面积分别记为S1,S2,则S1+S2的值等于( )
A.2π
B.4π
C.8π
D.16π
8.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载,如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图②的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
9.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方3
km处,过了20
s,飞机距离这个男孩头顶5
km(如图).这一过程中飞机飞行的速度是每秒________千米( )
A.0.2
B.2
C.0.4
D.4
10.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的面积分别为2,5,1,2,则最大的正方形E的面积是( )
A.6
B.8
C.9
D.10
二.填空题(共8小题,3
8=24)
11.无盖圆柱形杯子的展开图如图所示.将一根长为20
cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有________cm.
12.
在△ABC中,∠C=90°,一条直角边长为4
cm,斜边长比另一条直角边长长1
cm,则△ABC的周长是________.
13.在Rt△ABC中,斜边长BC=3,AB2+AC2+BC2的值为________.
14.在△ABC中,若∠B=90°,∠A,∠B,∠C的对边分别是a,b,c,且a=7,b=25,则c的长为________.
15.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是________.
16.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为________.
17.我国三国时期的数学家赵爽为了验证勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图①所示.在图②中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,
则正方形EFGH的边长为________.
18.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,最大正方形的边长为2
cm,则正方形A,B,C,D的面积和是____
cm2.
三.解答题(共7小题,
46分)
19.(6分)
有一根高为16
m的电线杆在点A处断裂,电线杆顶部点C落到离电线杆底部B点8
m的地方,求电线杆的断裂处点A离地面有多高?
20.(6分)
如图,在△ABC中,∠C=90°,AC=4,BC=8.
(1)用直尺和圆规作AB的垂直平分线(保留作图痕迹,不要求写作法);
(2)若(1)中所作的垂直平分线交BC于点D,求BD的长.
21.(6分)
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若AB=5
cm,BC=3
cm,求BD的长.
22.(6分)
用如图①的四个形状、大小完全一样的直角三角形拼一拼,摆一摆,可以摆成如图②的正方形.请你用这个图形验证勾股定理.
图①
图②
23.(6分)
在一棵树的10
m高处有两只猴子,其中一只爬下树走向离树20
m的池塘,而另一只爬向树顶后直扑池塘(运动路线看作直线),如果两只猴子经过的距离相等,问这棵树有多高?
24.(8分)
如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
25.(8分)
.如图,将长方形纸片ABCD的一边AD向下折叠,点D落在BC边的点F处.已知AB=8
cm,BC=10
cm,求EC的长.
参考答案
1-5DACCC
6-10AACAD
11.
5
12.
20cm
13.
18
14.
24
15.
4
16.
17.
10
18.
4
19.
解:设AB长为x
m,
则有x2+82=(16-x)2,
解得x=6,
故断裂处点A离地面有6
m
20.
解:(1)所作AB的垂直平分线如图所示.
(2)如图,连接AD,由作图可知AD=BD,设BD=x,
则AD=x,CD=8-x.因为∠C=90°,
所以由勾股定理可得AC2+CD2=AD2.
因为AC=4,所以42+(8-x)2=x2,解得x=5.
所以BD=5.
21.
解:由勾股定理可以得到AB2=AC2+BC2,∴AC=4,
由S△ABC=AC·BC=AB·CD,
即×4×3=×5×CD,∴CD=,
∴BD2=BC2-CD2=,
∴BD=(cm)
22.
证明:因为图②中大正方形的面积可以表示为c2+4×ab,也可以表示为(a+b)2,
所以c2+4×ab=(a+b)2.
整理,得c2+2ab=a2+2ab+b2.
即a2+b2=c2.
23.
解:如图,点B为树顶,D处有两只猴子,则AD=10
m,C为池塘,则AC=20
m.
设BD的长为x
m,则树的高度为(10+x)m.
∵AC+AD=BD+BC,∴BC=20+10-x=30-x.
在△ACB中,∠A=90°,∴AC2+AB2=BC2,
即202+(10+x)2=(30-x)2,
解得x=5.
即树高为15
m
24.
解:在△ABC中,作AD⊥BC于点D,设BD=x,则CD=14-x.
由勾股定理,得AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
所以152-x2=132-(14-x)2.
解得x=9.
在Rt△ABD中,AD2=AB2-BD2=152-92=144,
所以AD=12.
所以S△ABC=BC·AD=×14×12=84.
25.
解:根据题意,得△AFE≌△ADE,
所以AF=AD=BC=10
cm,EF=ED.
所以EF+EC=DC=AB=8
cm.
在Rt△ABF中,根据勾股定理得BF2=AF2-AB2=102-82=36,
所以BF=6
cm.所以FC=BC-BF=10-6=4(cm).
设EC=x
cm,则EF=DC-EC=(8-x)
cm.
在Rt△EFC中,根据勾股定理得EC2+FC2=EF2,
即x2+42=(8-x)2.解这个方程,得x=3,即EC的长为3
cm.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
