【数学】1.1.3《算法的三种基本逻辑结构和框图表示(第二课时)》课件(新人教b版必修3)
文档属性
| 名称 | 【数学】1.1.3《算法的三种基本逻辑结构和框图表示(第二课时)》课件(新人教b版必修3) |

|
|
| 格式 | rar | ||
| 文件大小 | 777.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 17:18:32 | ||
图片预览



文档简介
(共19张PPT)
普通高中课程标准数学3(必修)
书 山 有 路 勤 为 径,学 海 无 崖 苦 作 舟
少 小 不 学 习,老 来 徒 伤 悲
成功=艰苦的劳动+正确的方法+少谈空话
天才就是百分之一的灵感,百分之九十九的汗水!
天 才 在 于 勤 奋,努 力 才 能 成 功!
勤劳的孩子展望未来, 但懒惰的孩子享受现在!!!
什 么 也 不 问 的 人 什 么 也 学 不 到 !!!
怀 天 下 , 求 真 知 , 学 做 人
1.1. 3 算法的三种基本逻辑结构和框图表示(约3课时)
第一章 算法初步
第二课时
一、复习引入
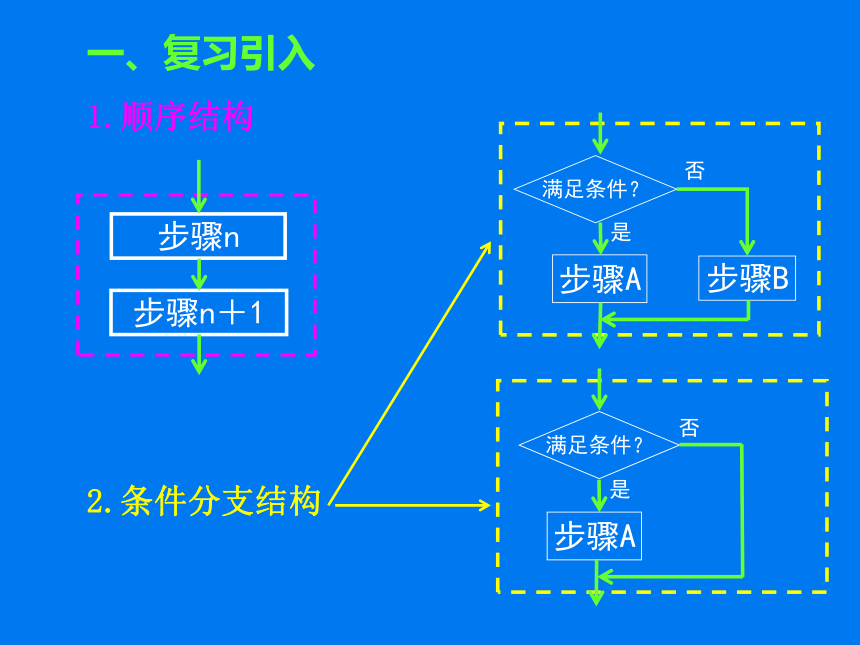
1.顺序结构
2.条件分支结构
步骤n
步骤n+1
是
是
步骤A
步骤B
满足条件?
否
步骤A
满足条件?
否
二、提出问题
太阳每天从东边升起,从西边落下,周而复始,循环不断;我们的课程表每星期循环一次;正弦函数每经过正弦值开始重复,这些都是循环问题,循环问题我们可以用循环结构框图表示。
三、概念形成
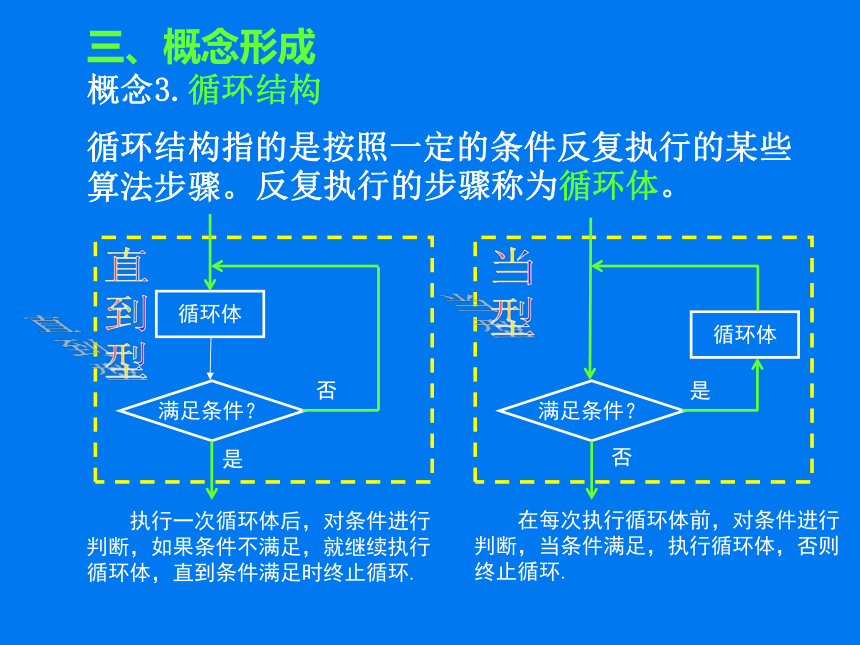
概念3.循环结构
循环结构指的是按照一定的条件反复执行的某些算法步骤。
反复执行的步骤称为循环体。
循环体
满足条件?
否
是
循环体
满足条件?
否
是
执行一次循环体后,对条件进行
判断,如果条件不满足,就继续执行
循环体,直到条件满足时终止循环.
在每次执行循环体前,对条件进行
判断,当条件满足,执行循环体,否则
终止循环.
三、概念形成
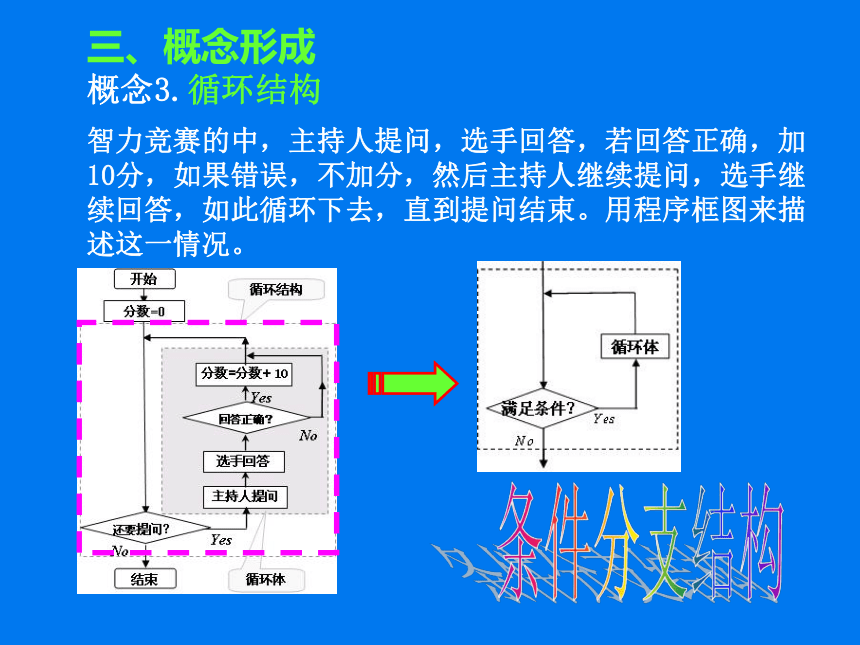
智力竞赛的中,主持人提问,选手回答,若回答正确,加10分,如果错误,不加分,然后主持人继续提问,选手继续回答,如此循环下去,直到提问结束。用程序框图来描述这一情况。
概念3.循环结构
三、概念形成
概念3.循环结构
探究
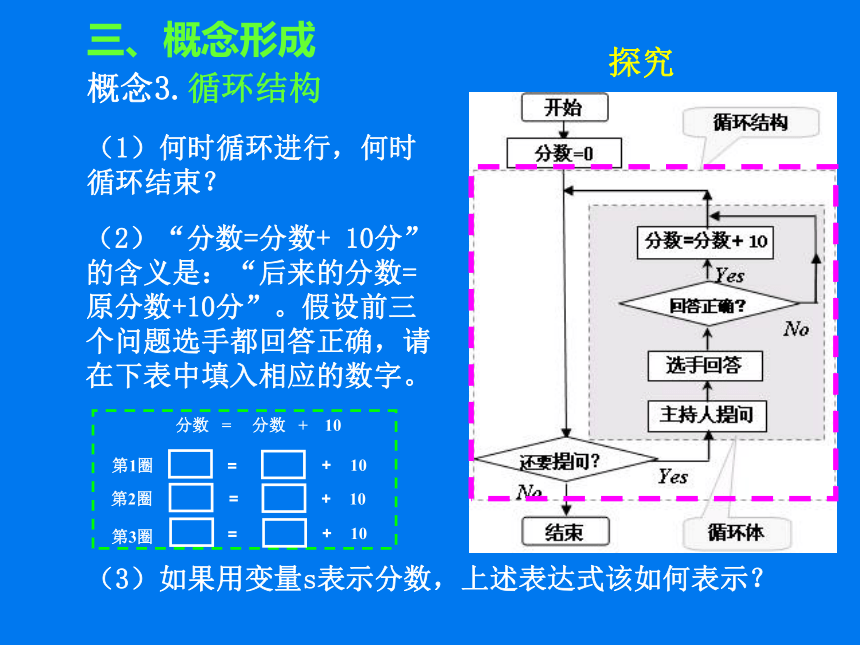
(1)何时循环进行,何时循环结束?
(2)“分数=分数+ 10分”的含义是:“后来的分数=原分数+10分”。假设前三个问题选手都回答正确,请在下表中填入相应的数字。
分数 = 分数 + 10
第1圈
第3圈
第2圈
=
+ 10
+ 10
+ 10
=
=
(3)如果用变量s表示分数,上述表达式该如何表示?
四、应用举例
例1.设计一个计算1+2+3+…+100的值的算法,并画出程序框图。
第一步:确定首数a,尾数b,项数n;
第二步:利用公式“S=n (a+b) /2”求和;
第三步:输出求和结果。
算法1:
开始
结束
输入a,b,n
S=n(a+b)/2
输出S
四、应用举例
例1.设计一个计算1+2+3+…+100的值的算法,并画出程序框图。
开始
i=1
S=0
i=i+1
S=S+i
i≤100
输出S
结束
否
是
第1步,0+1=1.
第2步,1+2=3.
第3步,3+3=6.
第4步,6+4=10.
……
第100步,4950+100=5050.
算法2:
第一步,令i=1,S=0.
第二步,若i ≤100成立,则执
行第三步;否则,输出S,结束算法.
第三步,S=S+i.
第四步,i=i+1,返回第二步.
当型循环结构
四、应用举例
例1.设计一个计算1+2+3+…+100的值的算法,并画出程序框图。
循环结构
四、应用举例
i = i + 1
Sum=Sum + i
解决方法就是加上一个判断,判断是否已经加到了100,如果加到了则退出,否则继续加。
直到型结构
当型结构
i = i + 1
Sum=Sum + i
是
否
i = i + 1
Sum=Sum + i
否
是
i<100
i>=100
请填上判断的条件。
在解题的过程中,用累加变量S表示
每一步的计算结果,即把S+i的结果仍记
为S,从而把第i步表示为S=S+i,其中S
的初始值为0,i依次取1,2,…,100.
由于i同时记录了循环的次数,所以也称
为计数变量。
循环结构中都有一个计数变量和累加变量,
计数变量用以记录循环次数,同时它的取值还
用于判断循环是否终止,累加变量用于输出结
果,累加变量和计数变量一般是同步执行的,
累加一次,计数一次.
四、应用举例
例2.某工厂2005年的年生产总值为200万元,技术革新后预计以后每年的年生产总值都比上一年增长5℅.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.
算法步骤:
第一步,输入2005年的年生产总值。
第二步,计算下一年的年生产总值。
第三步,判断所得的结果是否大于300。若是,则输出该年的年份;否则,返回第二步。
结束
开始
输出n
a=200
t=0.05a
a=a+t
n=n+1
a>300
Y
n=2005
N
(1)确定循环体:设a为某年的年生产总值,t为年生产总值的年增长量,n为年份,则循环体为t=0.05a,a=a+t,n=n+1。
(2)初始化变量: n=2005, a=200.
(3)循环控制条件: a>300
四、应用举例
结束
开始
输入n
a=200
t=0.05a
a=a+t
n=n+1
a>300
Y
n=2005
N
结束
开始
输入n
a=200
t=0.05a
a=a+t
n=n+1
a≤300
N
n=2005
Y
直到型
当型
五、课堂练习
课本第14页,练习A,1,2,3
开始
i=1
S=0
i=i+1
S=S+i
i≤10
输出S
结束
否
是
课本第14页,练习A,1参考框图
五、课堂练习
课本第14页,练习A,1,2,3
结束
开始
n=10
输出S的值
S=0
i=1
S=S+1/i
i=i+1
i≤n
Y
N
第14页,练习A,2参考框图
五、课堂练习
课本第14页,练习A,1,2,3
第14页,练习A,3参考框图
结束
开始
输出S的值
x=1
y=x2
x=x+1
x≤10
Y
N
六、课堂总结
1、循环结构的特点
2、循环结构的框图表示
3、循环结构该注意的问题
避免死循环的出现,设置好进入(结束)循环体的条件。
当型和直到型
重复同一个处理过程
七、布置作业
课本第14页,练习B,1,2,3
弹性作业:课本15页,习题1-1A,B
下课
普通高中课程标准数学3(必修)
书 山 有 路 勤 为 径,学 海 无 崖 苦 作 舟
少 小 不 学 习,老 来 徒 伤 悲
成功=艰苦的劳动+正确的方法+少谈空话
天才就是百分之一的灵感,百分之九十九的汗水!
天 才 在 于 勤 奋,努 力 才 能 成 功!
勤劳的孩子展望未来, 但懒惰的孩子享受现在!!!
什 么 也 不 问 的 人 什 么 也 学 不 到 !!!
怀 天 下 , 求 真 知 , 学 做 人
1.1. 3 算法的三种基本逻辑结构和框图表示(约3课时)
第一章 算法初步
第二课时
一、复习引入
1.顺序结构
2.条件分支结构
步骤n
步骤n+1
是
是
步骤A
步骤B
满足条件?
否
步骤A
满足条件?
否
二、提出问题
太阳每天从东边升起,从西边落下,周而复始,循环不断;我们的课程表每星期循环一次;正弦函数每经过正弦值开始重复,这些都是循环问题,循环问题我们可以用循环结构框图表示。
三、概念形成
概念3.循环结构
循环结构指的是按照一定的条件反复执行的某些算法步骤。
反复执行的步骤称为循环体。
循环体
满足条件?
否
是
循环体
满足条件?
否
是
执行一次循环体后,对条件进行
判断,如果条件不满足,就继续执行
循环体,直到条件满足时终止循环.
在每次执行循环体前,对条件进行
判断,当条件满足,执行循环体,否则
终止循环.
三、概念形成
智力竞赛的中,主持人提问,选手回答,若回答正确,加10分,如果错误,不加分,然后主持人继续提问,选手继续回答,如此循环下去,直到提问结束。用程序框图来描述这一情况。
概念3.循环结构
三、概念形成
概念3.循环结构
探究
(1)何时循环进行,何时循环结束?
(2)“分数=分数+ 10分”的含义是:“后来的分数=原分数+10分”。假设前三个问题选手都回答正确,请在下表中填入相应的数字。
分数 = 分数 + 10
第1圈
第3圈
第2圈
=
+ 10
+ 10
+ 10
=
=
(3)如果用变量s表示分数,上述表达式该如何表示?
四、应用举例
例1.设计一个计算1+2+3+…+100的值的算法,并画出程序框图。
第一步:确定首数a,尾数b,项数n;
第二步:利用公式“S=n (a+b) /2”求和;
第三步:输出求和结果。
算法1:
开始
结束
输入a,b,n
S=n(a+b)/2
输出S
四、应用举例
例1.设计一个计算1+2+3+…+100的值的算法,并画出程序框图。
开始
i=1
S=0
i=i+1
S=S+i
i≤100
输出S
结束
否
是
第1步,0+1=1.
第2步,1+2=3.
第3步,3+3=6.
第4步,6+4=10.
……
第100步,4950+100=5050.
算法2:
第一步,令i=1,S=0.
第二步,若i ≤100成立,则执
行第三步;否则,输出S,结束算法.
第三步,S=S+i.
第四步,i=i+1,返回第二步.
当型循环结构
四、应用举例
例1.设计一个计算1+2+3+…+100的值的算法,并画出程序框图。
循环结构
四、应用举例
i = i + 1
Sum=Sum + i
解决方法就是加上一个判断,判断是否已经加到了100,如果加到了则退出,否则继续加。
直到型结构
当型结构
i = i + 1
Sum=Sum + i
是
否
i = i + 1
Sum=Sum + i
否
是
i<100
i>=100
请填上判断的条件。
在解题的过程中,用累加变量S表示
每一步的计算结果,即把S+i的结果仍记
为S,从而把第i步表示为S=S+i,其中S
的初始值为0,i依次取1,2,…,100.
由于i同时记录了循环的次数,所以也称
为计数变量。
循环结构中都有一个计数变量和累加变量,
计数变量用以记录循环次数,同时它的取值还
用于判断循环是否终止,累加变量用于输出结
果,累加变量和计数变量一般是同步执行的,
累加一次,计数一次.
四、应用举例
例2.某工厂2005年的年生产总值为200万元,技术革新后预计以后每年的年生产总值都比上一年增长5℅.设计一个程序框图,输出预计年生产总值超过300万元的最早年份.
算法步骤:
第一步,输入2005年的年生产总值。
第二步,计算下一年的年生产总值。
第三步,判断所得的结果是否大于300。若是,则输出该年的年份;否则,返回第二步。
结束
开始
输出n
a=200
t=0.05a
a=a+t
n=n+1
a>300
Y
n=2005
N
(1)确定循环体:设a为某年的年生产总值,t为年生产总值的年增长量,n为年份,则循环体为t=0.05a,a=a+t,n=n+1。
(2)初始化变量: n=2005, a=200.
(3)循环控制条件: a>300
四、应用举例
结束
开始
输入n
a=200
t=0.05a
a=a+t
n=n+1
a>300
Y
n=2005
N
结束
开始
输入n
a=200
t=0.05a
a=a+t
n=n+1
a≤300
N
n=2005
Y
直到型
当型
五、课堂练习
课本第14页,练习A,1,2,3
开始
i=1
S=0
i=i+1
S=S+i
i≤10
输出S
结束
否
是
课本第14页,练习A,1参考框图
五、课堂练习
课本第14页,练习A,1,2,3
结束
开始
n=10
输出S的值
S=0
i=1
S=S+1/i
i=i+1
i≤n
Y
N
第14页,练习A,2参考框图
五、课堂练习
课本第14页,练习A,1,2,3
第14页,练习A,3参考框图
结束
开始
输出S的值
x=1
y=x2
x=x+1
x≤10
Y
N
六、课堂总结
1、循环结构的特点
2、循环结构的框图表示
3、循环结构该注意的问题
避免死循环的出现,设置好进入(结束)循环体的条件。
当型和直到型
重复同一个处理过程
七、布置作业
课本第14页,练习B,1,2,3
弹性作业:课本15页,习题1-1A,B
下课
