青岛版八年级数学下册7.6立方根课件 (共29张PPT)
文档属性
| 名称 | 青岛版八年级数学下册7.6立方根课件 (共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
图片预览





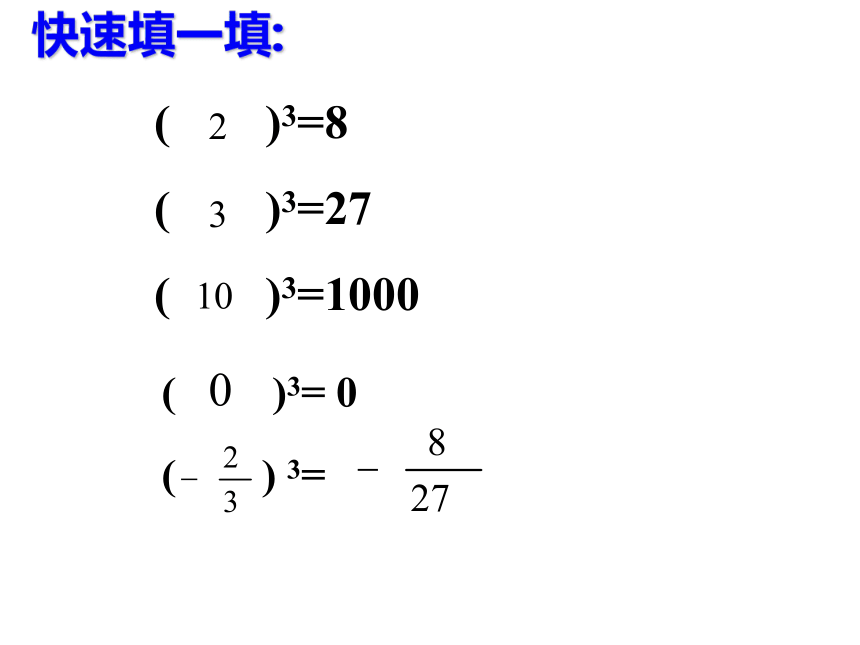



文档简介
(共29张PPT)
§7.6立方根
第7章:实数
1.
什么叫平方根?
如果x2=a,那么x是
a的平方根,
复习回顾
2.
平方根有什么性质?
(1)一个正数有两个平方根,这两个平方根互为相反数。
(2)零的平方根是零。
(3)负数没有平方根.
3.什么叫做开平方运算?
求一个数的平方根的运算,叫开平方。
(1)64的算术平方根是
;
(2)
的平方根是
;
(3)若a的平方根只有一个,那么a
=
;
(4)若数
b
的一个平方根是
1.2,
那么
b
的另一个平方根是
;
(5)
的算术平方根是
;
8
0
-1.2
3
巩固练习:
问题
:
要制作一个体积为125m3的正方体形状的包装箱,这种包装箱的边长应当是多少?
若设这个正方体的边长
是x,应该怎样列方程呢?
解:设这种包装箱的边长为
x
m,则:
x3
=
125
因为
53
=125,所以正方体包装箱的棱长为5米。
这就是要求一个数,使它的立方等于125。你能算出来吗?
(
)3=8
(
)3=27
(
)3=1000
2
3
10
快速填一填:
新知探索
一、什么叫做立方根?
一般的,如果x3=a,那么x叫做a
的立方根,或三次方根。
二、立方根的符号表示
例如:53
=125,所以5是125的立方根。
三、什么叫做开立方?
求一个数的立方根的运算叫做开立方。
四、怎样求一个数的立方根呢?
先考虑哪个数的立方等于已知数。
求下列各数的立方根:
新知探索
由此你发现了什么结论?
1、一个正数有一个正的立方根;
2、一个负数有一个负的立方根,
3、零的立方根是零。
五、立方根的特征
讨论:你能归纳出平方根和立方根的异同点吗?
4、互为相反数两个数的立方根仍然是互为相反数。
①同号性
②唯一性
区别:
(1)定义不同:
一个正数有两个平方根,
一个正数有一个立方根;
一个负数没有平方根,
一个负数有一个立方根.
(2)个数不同:
(3)表示法不同
(4)被开方数的取值范围不同
议一议
,
,
,
你会区别下列的数吗?
例题精讲
例题精讲
练一练
1.判断下列说法是否正确,并说明理由
x
(2)
25的平方根是5
x
(3)
-64没有立方根
x
(4)
-4的平方根是
x
(5)
0的平方根和立方根都是0
√
立方根是它本身的数有那些?
有1,
-1,
0
平方根是它本身的数呢?
只有0
想一想
(
)
(
)
(
)
(
)
(
)
(1)
算术平方根是它本身的数呢?
有0和1
2
-2
-0.1
a
引伸探究3
因为
=
,
=
.
=
-7
-7
=
-8
-8
(1)
(2)
从上面的例题可知:
由此可得出:
也就是把根号里的“负号”直接从根号里面提到了根号“外面”
。即
特别注意:平方根不能这样哟!
由此得出求一个负数的立方根的一般方法:
也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。
互为相反数的数的立方根也互为相反数
探究4
先填写下表,再回答问题:
0.01
0.1
1
10
100
从上面表格中你发现什么?
被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.
被开方数的小数点向左(或向右)每移动3位,它的立方根的小数点相应地向左(或向右)移动1位.
a
0.000001
0.001
1
1000
1000000
课堂练习:
1、下列运算中不正确的是(
)
(1)1的平方根是______;立方根为______;算术平方根为_________.
(2)平方根是它本身的数是__________.
(3)立方根是其本身的数是___________.
(4)算术平方根是其本身的数是________.
(5)
的立方根为
.
(6)
的平方根为
.
(7)
的立方根为
.
填空练习:
±1
1
1
0
±1
,
0
1
,
0
-2
-2
±2
2.若一个数的平方根为±8,则这个数的立方根
是
。
4.
若a2=(-5)2,b3=(-5)3,则a+b的值为
。
3.
如果一个数的立方根等于这个数的算术平方根,
那么这个数是(
)
(A)0
(B)0或1
(C)1
(D)±1或0
6.
若x2-9=0,y3+27=0,则点P(y,-x)
在第
象限
4
B
0或-10
B
二或三
课堂练习:
7.你能求出下列各式中的未知数x吗?
(1)
x3=729
(2)(x-1)3=125
解:
∴x=9
∴x-1=5
X=6
(3)
(4)
∴X=66
∴x=8
平方根、算术平方根
与立方根有何区别
?
正数的平方根有两个;
0的平方根是0;
负数没有平方根
正数的算术平方根是正数;
0的算术平方根是0;
负数没有算术平方根
正数的立方根是正数;
0的立方根是0;负数的立方根是负数
a为任意实数
小结
平方根
算术平方根
立方根
表示方法
a的取值
性质
被开方数
立方根
根指数
注意:根指数是3
时,绝对不能省略不写。
提醒你
再见
§7.6立方根
第7章:实数
1.
什么叫平方根?
如果x2=a,那么x是
a的平方根,
复习回顾
2.
平方根有什么性质?
(1)一个正数有两个平方根,这两个平方根互为相反数。
(2)零的平方根是零。
(3)负数没有平方根.
3.什么叫做开平方运算?
求一个数的平方根的运算,叫开平方。
(1)64的算术平方根是
;
(2)
的平方根是
;
(3)若a的平方根只有一个,那么a
=
;
(4)若数
b
的一个平方根是
1.2,
那么
b
的另一个平方根是
;
(5)
的算术平方根是
;
8
0
-1.2
3
巩固练习:
问题
:
要制作一个体积为125m3的正方体形状的包装箱,这种包装箱的边长应当是多少?
若设这个正方体的边长
是x,应该怎样列方程呢?
解:设这种包装箱的边长为
x
m,则:
x3
=
125
因为
53
=125,所以正方体包装箱的棱长为5米。
这就是要求一个数,使它的立方等于125。你能算出来吗?
(
)3=8
(
)3=27
(
)3=1000
2
3
10
快速填一填:
新知探索
一、什么叫做立方根?
一般的,如果x3=a,那么x叫做a
的立方根,或三次方根。
二、立方根的符号表示
例如:53
=125,所以5是125的立方根。
三、什么叫做开立方?
求一个数的立方根的运算叫做开立方。
四、怎样求一个数的立方根呢?
先考虑哪个数的立方等于已知数。
求下列各数的立方根:
新知探索
由此你发现了什么结论?
1、一个正数有一个正的立方根;
2、一个负数有一个负的立方根,
3、零的立方根是零。
五、立方根的特征
讨论:你能归纳出平方根和立方根的异同点吗?
4、互为相反数两个数的立方根仍然是互为相反数。
①同号性
②唯一性
区别:
(1)定义不同:
一个正数有两个平方根,
一个正数有一个立方根;
一个负数没有平方根,
一个负数有一个立方根.
(2)个数不同:
(3)表示法不同
(4)被开方数的取值范围不同
议一议
,
,
,
你会区别下列的数吗?
例题精讲
例题精讲
练一练
1.判断下列说法是否正确,并说明理由
x
(2)
25的平方根是5
x
(3)
-64没有立方根
x
(4)
-4的平方根是
x
(5)
0的平方根和立方根都是0
√
立方根是它本身的数有那些?
有1,
-1,
0
平方根是它本身的数呢?
只有0
想一想
(
)
(
)
(
)
(
)
(
)
(1)
算术平方根是它本身的数呢?
有0和1
2
-2
-0.1
a
引伸探究3
因为
=
,
=
.
=
-7
-7
=
-8
-8
(1)
(2)
从上面的例题可知:
由此可得出:
也就是把根号里的“负号”直接从根号里面提到了根号“外面”
。即
特别注意:平方根不能这样哟!
由此得出求一个负数的立方根的一般方法:
也就是说,求一个负数的立方根,可以先求出这个负数的绝对值的立方根,然后再取它的相反数。
互为相反数的数的立方根也互为相反数
探究4
先填写下表,再回答问题:
0.01
0.1
1
10
100
从上面表格中你发现什么?
被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.
被开方数的小数点向左(或向右)每移动3位,它的立方根的小数点相应地向左(或向右)移动1位.
a
0.000001
0.001
1
1000
1000000
课堂练习:
1、下列运算中不正确的是(
)
(1)1的平方根是______;立方根为______;算术平方根为_________.
(2)平方根是它本身的数是__________.
(3)立方根是其本身的数是___________.
(4)算术平方根是其本身的数是________.
(5)
的立方根为
.
(6)
的平方根为
.
(7)
的立方根为
.
填空练习:
±1
1
1
0
±1
,
0
1
,
0
-2
-2
±2
2.若一个数的平方根为±8,则这个数的立方根
是
。
4.
若a2=(-5)2,b3=(-5)3,则a+b的值为
。
3.
如果一个数的立方根等于这个数的算术平方根,
那么这个数是(
)
(A)0
(B)0或1
(C)1
(D)±1或0
6.
若x2-9=0,y3+27=0,则点P(y,-x)
在第
象限
4
B
0或-10
B
二或三
课堂练习:
7.你能求出下列各式中的未知数x吗?
(1)
x3=729
(2)(x-1)3=125
解:
∴x=9
∴x-1=5
X=6
(3)
(4)
∴X=66
∴x=8
平方根、算术平方根
与立方根有何区别
?
正数的平方根有两个;
0的平方根是0;
负数没有平方根
正数的算术平方根是正数;
0的算术平方根是0;
负数没有算术平方根
正数的立方根是正数;
0的立方根是0;负数的立方根是负数
a为任意实数
小结
平方根
算术平方根
立方根
表示方法
a的取值
性质
被开方数
立方根
根指数
注意:根指数是3
时,绝对不能省略不写。
提醒你
再见
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
