【数学】2.2.1《用样本的频率分布估计总体的分布2》课件(新人教b版必修3)
文档属性
| 名称 | 【数学】2.2.1《用样本的频率分布估计总体的分布2》课件(新人教b版必修3) |

|
|
| 格式 | rar | ||
| 文件大小 | 266.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览









文档简介
(共36张PPT)
2.2.1 用样本的频率分布估计总体的分布(二)
二、总体密度曲线
1.频率分布折线图
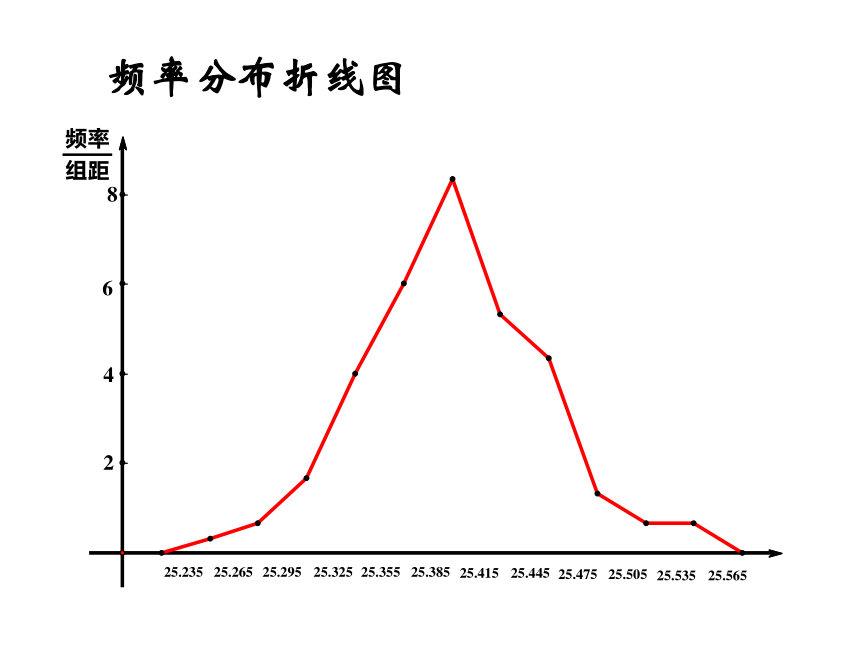
把频率分布直方图各个长方形上边的中点用线段连接起来,就得到频率分布折线图。
为了方便看图,一般习惯于把频率分布折线图画成与横轴相连,所以横轴上的左右两端点没有实际的意义。例如,前面的钢管内径的频率分布折线图,如图所示。
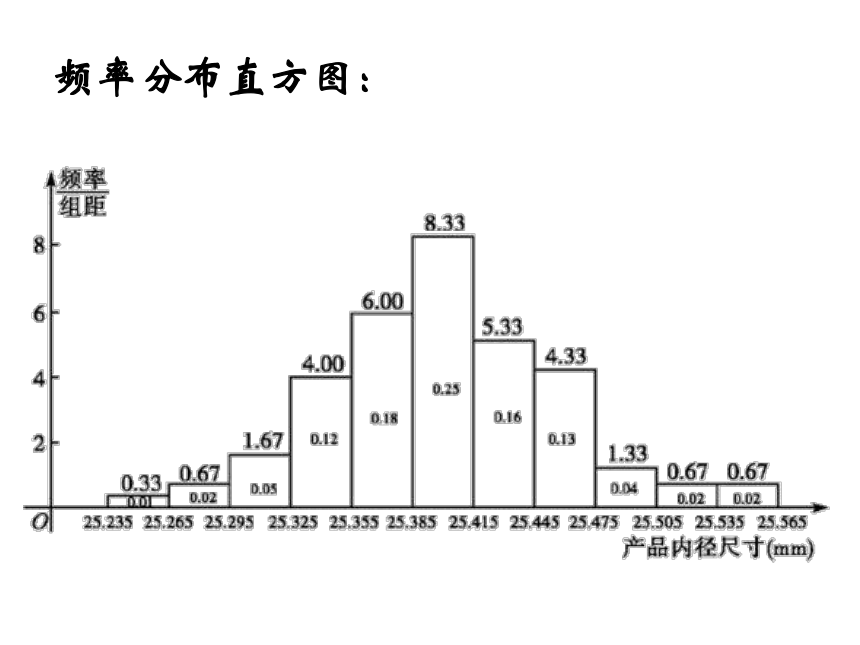
频率分布直方图:
频率分布折线图
2.总体密度曲线
如果样本容量越大,所分组数越多,上述图中表示的频率分布就越接近于总体在各个小组内所取值的个数与总数比值的大小。
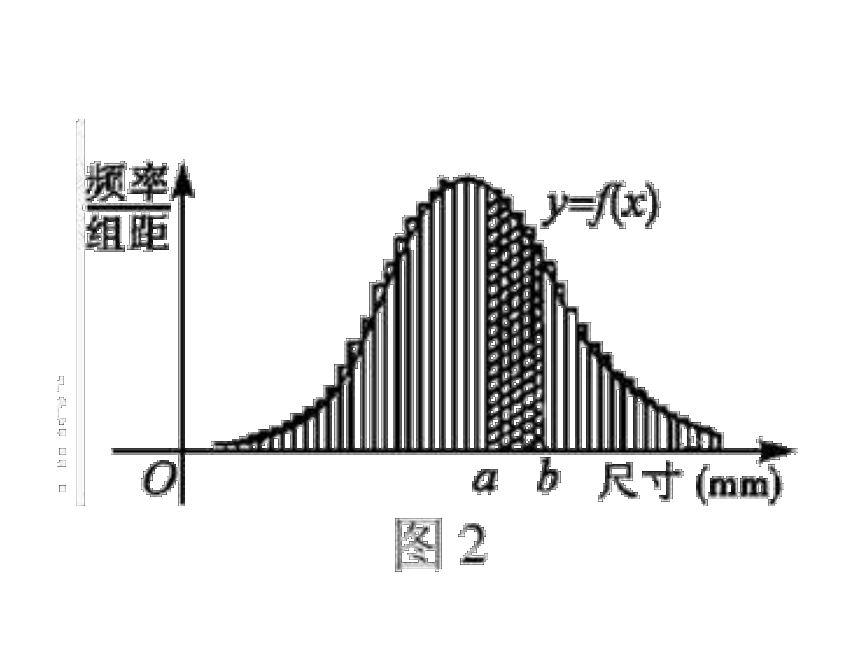
设想如果样本容量不断增大,分组的组距不断缩小,则频率分布直方图实际上越来越接近于总体的分布,它可以用一条光滑曲线y=f(x)来描绘,这条光滑曲线就叫做总体密度曲线。
总体密度曲线精确地反映了一个总体在各个区域内取值的规律。
产品尺寸落在(a,b)内的百分率就是图中带斜线部分的面积。
对前面钢管内径的例子来说,总体密度曲线呈中间高两边低的“钟”形分布,总体的数据大致呈对称分布,并且大部分数据都集中在靠近中间的区间内 。
例:对于样本频率分布折线图与总体密度曲线的关系,下列说法中正确的是( )
(A)频率分布折线图与总体密度曲线无关
(B)频率分布折线图就是总体密度曲线
(C)样本容量很大的频率分布折线图就是总体密度曲线
(D)如果样本容量无限增大,分组的组距无限减小,那么频率分布折线图就会无限接近于总体密度曲线
D
解析:总体密度曲线通常是用样本频率分布估计出来的;因为如果样本容量无限增大,分组的组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线,这条曲线就是总体密度曲线,故选D.
(1)总体密度曲线与总体分布相互唯一确定,如果总体分布已知,就可以得到总体密度曲线的函数表达式,从而用函数的理论去研究它。但我们所面临的情况是总体分布未知,因此,我们只能通过样本频率分布折线图近似表示总体密度曲线,当然还可以用其他方法估计总体密度曲线,但不能够通过样本数据准确地画出总体密度曲线。
进一步理解:
(2)总体密度曲线的实际意义在于:
总体密度曲线与x轴,直线x=a,x=b围成的面积等于x在[a,b]取值时的概率.
2.茎叶图
茎叶图也是用来表示数据的一种图,茎是中间的一列数,叶是从茎上生长出来的数.
例.甲、乙两篮球运动员在上赛季每场比赛的得分如下,试比较这两位运动员的得分水平.
甲: 12,15,24,25,31,31,36,36,37,39,44,49,50.
乙: 8,13,14,16,23,26,28,33,38,39,51
解:画出两人得分的茎叶图
茎叶图的中间部分像一颗植物的茎,两边部分像这颗植物上长出来的叶子。
用中间的数字表示两位运动员得分的十位数,两边的数字分布表示两个人各场得分的个位数,例如 3| 389 就表示了33,38,39这3个数据。
从这个茎叶图可以看出甲运动员的得分大致对称平均得分及中位数、众数都是30多分;乙运动员的得分除一个51外,也大致对称,平均得分及中位数、众数都是20多分,因此甲运动员发挥比较稳定,总体得分情况比乙好.
画茎叶图的步骤
S1 将每个数据分为茎(高位)和叶(低位)两部分;
S2 将最小茎和最大茎之间的数按大小次序排成一列,写在左(右)侧;
S3 将各个数据的叶按大小次序写在其茎右(左)侧。
几种表示样本分布的方法比较:
(1)频率分布表在数量表示上比较确切,但不够直观、形象,分析数据分布的总体态势不太方便;
(2)频率分布直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到频率分布表中看不清楚的数据模式,但是从频率分布直方图本身不能得出原始的数据内容,也就是说,把数据表示成直方图后,原有的具体数据信息就被抹掉了。
(3)频率分布折线图的优点是它反映了数据的变化趋势,如果样本容量不断增大,分组的组距不断缩小,那么折线图就趋向于总体密度曲线。
(4)用茎叶图刻画数据有两个优点:一是所有的信息都可以从这个茎叶图中得到;二是茎叶图便于记录和表示,能够展示数据的分布情况,但当样本数据较多或数据位数较多时,茎叶图就显得不太方便了。
例1.在某电脑杂志的一篇文章中,每个句子的字数如下:
10,28,31,17,23,27,18,15,26,24,20,19,36,27,14,25,22,11,24,27,17.
在某报纸的一篇文章中,每个句子的字数如下:
27,39,33,24,28,19,32,41,33,27,35,12,36,41,27,13,22,23,18,46,32,22。
(1)将这两组数据用茎叶图表示;
(2)将这两组数据进行比较分析,得到什么结论?
(1)将这两组数据用茎叶图表示;
(2)电脑杂志上每个句子的字数集中在10,30之间,中位数为22.5,而报纸上每个句子的字数集中在20,40之间,中位数为27.5,还可以看出电脑杂志上每个句子的平均字数比报纸上每个句子的平均字数要少,说明电脑杂志作为科普读物需要简洁明了、通俗易懂。
例2. 有人说:“茎叶图表示三位数以上的数据时不够方便”, 果真如此吗?请看下例:
现在能否用茎叶图来表示上述数据呢?
解:从上述数据可以看到它们的百位数字都是3,所不同的仅仅是十位和个位,而两位数据是可以作茎的,那么只需在茎的位置写上百位和十位,叶的位置上写上个位即可。
例3. 某运动员得分的茎叶图如下,试判断他的得分的中位数,众数及稳定程度.
解:从这个图可以直观的看出该运动员得分的中位数是36、众数是31与36,
且得分大都在20和40之间,分布较对称,集中程度高,说明其发挥比较稳定.
练习题:
1.在频率分布直方图中,小矩形的高表示( )
A.频率/样本容量
B.组距×频率
C.频率
D.频率/组距
D
2.在用样本频率估计总体分布的过程中,下列说法中正确的是( )
A.总体容量越大,估计越精确
B.总体容量越小,估计越精确
C.样本容量越大,估计越精确
D.样本容量越小,估计越精确
C
3.一个容量为20的样本数据,分组后组距与频数如下表.
组距 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 2 3 4 5 4 2
则样本在区间(-∞,50)上的频率为( )
A.0.5 B.0.25 C.0.6 D.0.7
D
4. 10个小球分别编有号码1,2,3,4,其中1号球4个,2号球2个,3号球3个,4号球1个,数0.4是指1号球占总体分布的( )
A.频数 B.频率
C.频率/组距 D.累计频率
B
5.已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是( )
A. [5.5,7.5) B. [7.5,9.5)
C. [9.5,11.5) D. [11.5,13.5)
D
6.频率分布直方图中,小长方体的面积等于( )
A.相应各组的频数
B.相应各组的频率
C.组数
D.组距
B
7.将容量为50的数据,按从小到大的顺序分为6组,如下表.
组号 1 2 3 4 5 6
频数 6 8 10 10 9 7
第3组的频率和前3组的累计频率是( )
A. 0.24和0.5 B. 0.2和0.48
C. 0.06和0.24 D. 0.14和0.48
B
8.从一群学生中抽取一个一定容量的样本对他们的学习成绩进行分析,已知不超过70分的人数为8人,其累计频率为0.4,则这样的样本容量是( )
A.20人 B.40人
C.70人 D.80人
A
9. 一个容量为n的样本分成若干组,已知某组的频数和频率分别是30和0.25,则n=____________.
120
10. 将100个数据分成8个组,其中有一组是9个数据,那么该组的频数是______,频率是____________.
9
0.09
11.从某校2100名学生随机抽取一个30名学生的样本,样本中每个学生用于课外作业的时间(单位:min)依次为:75,80,85,65,95,100,70,55,65,75,85,110,120,80,85,80,75,90,90,95,70,60,60,75,90,95,65,75,80,80.该校的学生中作业时间超过一个半小时(含一个半小时)的学生有____________人.
630
12.频率分布直方图中各小长方体的面积和为____________.
1
2.2.1 用样本的频率分布估计总体的分布(二)
二、总体密度曲线
1.频率分布折线图
把频率分布直方图各个长方形上边的中点用线段连接起来,就得到频率分布折线图。
为了方便看图,一般习惯于把频率分布折线图画成与横轴相连,所以横轴上的左右两端点没有实际的意义。例如,前面的钢管内径的频率分布折线图,如图所示。
频率分布直方图:
频率分布折线图
2.总体密度曲线
如果样本容量越大,所分组数越多,上述图中表示的频率分布就越接近于总体在各个小组内所取值的个数与总数比值的大小。
设想如果样本容量不断增大,分组的组距不断缩小,则频率分布直方图实际上越来越接近于总体的分布,它可以用一条光滑曲线y=f(x)来描绘,这条光滑曲线就叫做总体密度曲线。
总体密度曲线精确地反映了一个总体在各个区域内取值的规律。
产品尺寸落在(a,b)内的百分率就是图中带斜线部分的面积。
对前面钢管内径的例子来说,总体密度曲线呈中间高两边低的“钟”形分布,总体的数据大致呈对称分布,并且大部分数据都集中在靠近中间的区间内 。
例:对于样本频率分布折线图与总体密度曲线的关系,下列说法中正确的是( )
(A)频率分布折线图与总体密度曲线无关
(B)频率分布折线图就是总体密度曲线
(C)样本容量很大的频率分布折线图就是总体密度曲线
(D)如果样本容量无限增大,分组的组距无限减小,那么频率分布折线图就会无限接近于总体密度曲线
D
解析:总体密度曲线通常是用样本频率分布估计出来的;因为如果样本容量无限增大,分组的组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线,这条曲线就是总体密度曲线,故选D.
(1)总体密度曲线与总体分布相互唯一确定,如果总体分布已知,就可以得到总体密度曲线的函数表达式,从而用函数的理论去研究它。但我们所面临的情况是总体分布未知,因此,我们只能通过样本频率分布折线图近似表示总体密度曲线,当然还可以用其他方法估计总体密度曲线,但不能够通过样本数据准确地画出总体密度曲线。
进一步理解:
(2)总体密度曲线的实际意义在于:
总体密度曲线与x轴,直线x=a,x=b围成的面积等于x在[a,b]取值时的概率.
2.茎叶图
茎叶图也是用来表示数据的一种图,茎是中间的一列数,叶是从茎上生长出来的数.
例.甲、乙两篮球运动员在上赛季每场比赛的得分如下,试比较这两位运动员的得分水平.
甲: 12,15,24,25,31,31,36,36,37,39,44,49,50.
乙: 8,13,14,16,23,26,28,33,38,39,51
解:画出两人得分的茎叶图
茎叶图的中间部分像一颗植物的茎,两边部分像这颗植物上长出来的叶子。
用中间的数字表示两位运动员得分的十位数,两边的数字分布表示两个人各场得分的个位数,例如 3| 389 就表示了33,38,39这3个数据。
从这个茎叶图可以看出甲运动员的得分大致对称平均得分及中位数、众数都是30多分;乙运动员的得分除一个51外,也大致对称,平均得分及中位数、众数都是20多分,因此甲运动员发挥比较稳定,总体得分情况比乙好.
画茎叶图的步骤
S1 将每个数据分为茎(高位)和叶(低位)两部分;
S2 将最小茎和最大茎之间的数按大小次序排成一列,写在左(右)侧;
S3 将各个数据的叶按大小次序写在其茎右(左)侧。
几种表示样本分布的方法比较:
(1)频率分布表在数量表示上比较确切,但不够直观、形象,分析数据分布的总体态势不太方便;
(2)频率分布直方图能够很容易地表示大量数据,非常直观地表明分布的形状,使我们能够看到频率分布表中看不清楚的数据模式,但是从频率分布直方图本身不能得出原始的数据内容,也就是说,把数据表示成直方图后,原有的具体数据信息就被抹掉了。
(3)频率分布折线图的优点是它反映了数据的变化趋势,如果样本容量不断增大,分组的组距不断缩小,那么折线图就趋向于总体密度曲线。
(4)用茎叶图刻画数据有两个优点:一是所有的信息都可以从这个茎叶图中得到;二是茎叶图便于记录和表示,能够展示数据的分布情况,但当样本数据较多或数据位数较多时,茎叶图就显得不太方便了。
例1.在某电脑杂志的一篇文章中,每个句子的字数如下:
10,28,31,17,23,27,18,15,26,24,20,19,36,27,14,25,22,11,24,27,17.
在某报纸的一篇文章中,每个句子的字数如下:
27,39,33,24,28,19,32,41,33,27,35,12,36,41,27,13,22,23,18,46,32,22。
(1)将这两组数据用茎叶图表示;
(2)将这两组数据进行比较分析,得到什么结论?
(1)将这两组数据用茎叶图表示;
(2)电脑杂志上每个句子的字数集中在10,30之间,中位数为22.5,而报纸上每个句子的字数集中在20,40之间,中位数为27.5,还可以看出电脑杂志上每个句子的平均字数比报纸上每个句子的平均字数要少,说明电脑杂志作为科普读物需要简洁明了、通俗易懂。
例2. 有人说:“茎叶图表示三位数以上的数据时不够方便”, 果真如此吗?请看下例:
现在能否用茎叶图来表示上述数据呢?
解:从上述数据可以看到它们的百位数字都是3,所不同的仅仅是十位和个位,而两位数据是可以作茎的,那么只需在茎的位置写上百位和十位,叶的位置上写上个位即可。
例3. 某运动员得分的茎叶图如下,试判断他的得分的中位数,众数及稳定程度.
解:从这个图可以直观的看出该运动员得分的中位数是36、众数是31与36,
且得分大都在20和40之间,分布较对称,集中程度高,说明其发挥比较稳定.
练习题:
1.在频率分布直方图中,小矩形的高表示( )
A.频率/样本容量
B.组距×频率
C.频率
D.频率/组距
D
2.在用样本频率估计总体分布的过程中,下列说法中正确的是( )
A.总体容量越大,估计越精确
B.总体容量越小,估计越精确
C.样本容量越大,估计越精确
D.样本容量越小,估计越精确
C
3.一个容量为20的样本数据,分组后组距与频数如下表.
组距 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70)
频数 2 3 4 5 4 2
则样本在区间(-∞,50)上的频率为( )
A.0.5 B.0.25 C.0.6 D.0.7
D
4. 10个小球分别编有号码1,2,3,4,其中1号球4个,2号球2个,3号球3个,4号球1个,数0.4是指1号球占总体分布的( )
A.频数 B.频率
C.频率/组距 D.累计频率
B
5.已知样本:12,7,11,12,11,12,10,10,9,8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是( )
A. [5.5,7.5) B. [7.5,9.5)
C. [9.5,11.5) D. [11.5,13.5)
D
6.频率分布直方图中,小长方体的面积等于( )
A.相应各组的频数
B.相应各组的频率
C.组数
D.组距
B
7.将容量为50的数据,按从小到大的顺序分为6组,如下表.
组号 1 2 3 4 5 6
频数 6 8 10 10 9 7
第3组的频率和前3组的累计频率是( )
A. 0.24和0.5 B. 0.2和0.48
C. 0.06和0.24 D. 0.14和0.48
B
8.从一群学生中抽取一个一定容量的样本对他们的学习成绩进行分析,已知不超过70分的人数为8人,其累计频率为0.4,则这样的样本容量是( )
A.20人 B.40人
C.70人 D.80人
A
9. 一个容量为n的样本分成若干组,已知某组的频数和频率分别是30和0.25,则n=____________.
120
10. 将100个数据分成8个组,其中有一组是9个数据,那么该组的频数是______,频率是____________.
9
0.09
11.从某校2100名学生随机抽取一个30名学生的样本,样本中每个学生用于课外作业的时间(单位:min)依次为:75,80,85,65,95,100,70,55,65,75,85,110,120,80,85,80,75,90,90,95,70,60,60,75,90,95,65,75,80,80.该校的学生中作业时间超过一个半小时(含一个半小时)的学生有____________人.
630
12.频率分布直方图中各小长方体的面积和为____________.
1
