【数学】2.2.2《用样本的数字特征估计总体的数字特征2》课件(新人教b版必修3)
文档属性
| 名称 | 【数学】2.2.2《用样本的数字特征估计总体的数字特征2》课件(新人教b版必修3) |

|
|
| 格式 | rar | ||
| 文件大小 | 95.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
2.2.2 用样本的数字特征估计总体的数字特征(二)
二、用样本的标准差估计总体的标准差
数据的离散程度可以用极差、方差或标准差来描述。
为了表示样本数据的单位表示的波动幅度,通常要求出样本方差或者它的算术平方根.
(1)方差:设在一组数据,x1,x2,…,xn中,各数据与它们的平均数x的差的平方分别是
来衡量这组数据的波动大小,并把它叫做这组数据的方差,一组数据方差越大,则这组数据波动越大。
那么我们用它们的平均数,即
(2)标准差:我们把数据的方差的算术平方根叫做这组数据的标准差,它也是一个用来衡量一组数据的波动大小的重要的量。
计算标准差的算法:
S2 算出每个样本数据与样本平均数的差
(i=1,2,……,n);
S1 算出样本数据的平均数x;
S3 算出 (i=1,2,…,n);
S4 算出 (i=1,2,…,n)这n个数的平均数,即为样本方差s2;
S5 算出方差的算术平方根,即为样本标准差s。
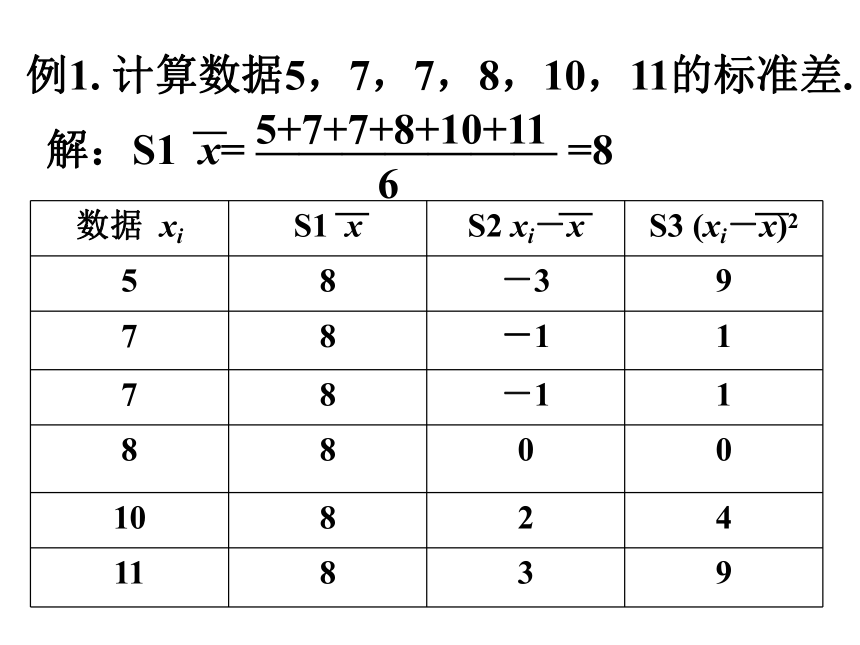
例1. 计算数据5,7,7,8,10,11的标准差.
解:S1 x= ——————— =8
5+7+7+8+10+11
6
数据 xi S1 x S2 xi-x S3 (xi-x)2
5 8 -3 9
7 8 -1 1
7 8 -1 1
8 8 0 0
10 8 2 4
11 8 3 9
S4 s2= ——————— =4;
9+1+1+0+4+9
6
S5 .
所以这组数据的标准差是2.
例2. 从某灯泡厂生产的一批灯泡中随机地抽取10只进行寿命测试,得数据如下(单位:h):
1458,1395,1562,1614,1351,1490,1478,1382,1536,1496
使用函数型计算器或计算机的Excel软件求样本的平均数x和样本的标准差。
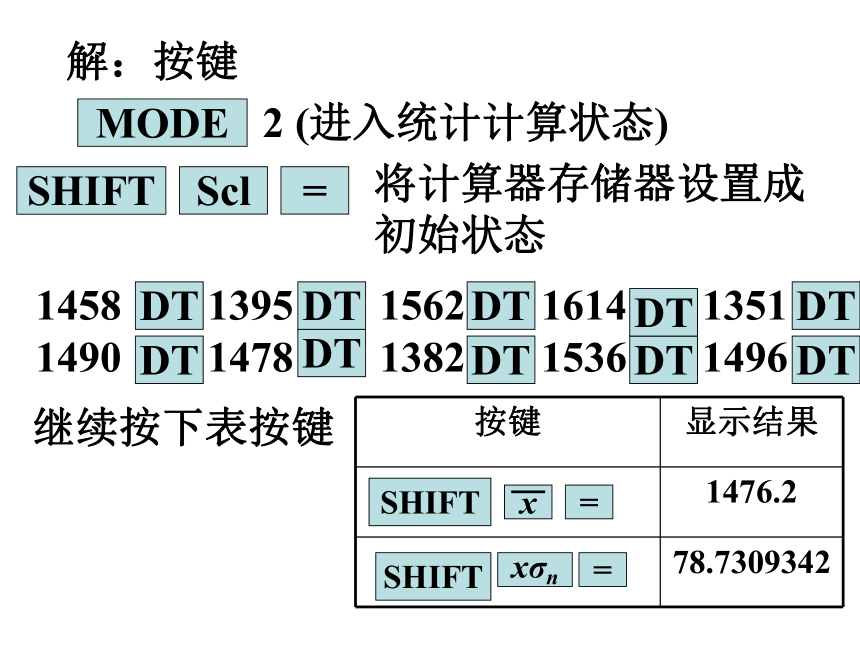
解:按键
MODE
2 (进入统计计算状态)
将计算器存储器设置成初始状态
SHIFT
Scl
=
1458 1395 1562 1614 1351 1490 1478 1382 1536 1496
DT
DT
DT
DT
DT
DT
DT
DT
DT
DT
继续按下表按键
按键 显示结果
1476.2
78.7309342
SHIFT
SHIFT
xσn
=
=
x
解2:打开Excel工作表,在一列输入数据,如将10个数据输入A1到A10单元格中.
(1)利用求和∑计算它们的和;
(2)用函数AVERAGE(A1:A10)求它们的平均数;
(3)用函数VARPA(A1:A10)求它们的方差;
(4)用开方函数Sqrt(方差)计算它们的标准差.
例3.计算数据89,93,88,91,94,90,88,87的方差和标准差。(标准差结果精确到0.1)
解:
.
所以这组数据的方差为5.5,标准差为2.3 .
例4. 从甲、乙两名学生中选拔一人乘积射击比赛,对他们的射击水平进行测试,两人在相同的条件下各射击10次,命中环数如下﹕
甲﹕7,8,6,8,6,5,8,10,7,4;
乙﹕9,5,7,8,7,6,8,6,7,7.
(1)计算甲、乙两人射击命中环数的平均数和标准差;
(2)比较两人的成绩,然后决定选择哪一人参赛.
解:(1)计算得x甲=7,x乙=7;
s甲=1.73,s乙=1.10.
(2)由(1)知,甲、乙两人平均成绩相等,但s乙(3)标准差和频率直方图的关系
从标准差的定义可知,如果样本各数据都相等,则标准差得0,这表明数据没有波动幅度,数据没有离散性;若个体的值与平均数的差的绝对值较大,则标准差也较大,表明数据的波动幅度也很大,数据的离散程度很高,因此标准差描述了数据对平均数的离散程度。
A B
样本数据 3 3 3 3 3 1 1 3 5 5
平均数 3 3
标准差 0 1.79
频率分布直方图
数据没有离散度
数据离散程度很高
再看钢管内径尺寸的例子,它的样本平均数是25.401,样本标准差是0.056,再直方图中用虚线标出平均数所在的位置,并画出距平均数两侧各一倍标准差和两倍标准差的区间。可以看到大约有70%的钢管内径尺寸落在距平均数两侧各一倍标准差的区间内,即(x-s, x+s)
大约有95%的钢管内径尺寸落在距平均数两侧各两倍标准差的区间内,即(x-2s, x+2s)。
s
s
2s
2s
x
的平均数为 ,
(2)新数据
方差为 .
,方差仍为 .
(1)新数据
的平均数为
,方差为 .
的平均数为
(3)新数据
如果数据
的平均数为 ,
方差为
,则
(4)方差的运算性质:
练习:
(3)若k1,k2,…, k8的方差为3,则2(k1-3),
2(k2-3), …, 2(k8-3)的方差为________
4
32
12
A
B
(7)在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为________
9.5,0.016
五、回顾小结:
1.用样本的数字特征估计总体的数字特征分两类:
用样本平均数估计总体平均数。
用样本方差、标准差估计总体方差、标准差。样本容量越大,估计就越精确。
2.方差、标准差描述一组数据围绕平均数波动的大小,反映了一组数据变化的幅度.
1.甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:t/hm2),试根据这组数据估计哪一种水稻品种的产量比较稳定。
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
解:甲品种的样本平均数为10,样本方差为 [(9.8-10)2 +(9.9-10)2+(10.1-10)2+ (10-10)2+(10.2-10)2]÷5=0.02.
乙品种的样本平均数也为10,样本方差为 [(9.4-10)2+(10.3-10)2+(10.8-10)2+ (9.7-10)2+(9.8-10)2]÷5=0.24.
因为0.24>0.02,
所以,由这组数据可以认为甲种水稻的产量比较稳定。
2.为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换。已知某校使用的100只日光灯在必须换掉前的使用天数如下,试估计这种日光灯的平均使用寿命和标准差。
天数 151~180 181~210 211~240 241~270 271~300 301~330 331~360 361~390
灯泡数 1 11 18 20 25 16 7 2
解:各组中值分别为165,195,225,285,315,345,375,由此算得平均数约为
165×1%+195×11%+225×18%+255×20%+285×25%+315×16%+345×7%+375×2%=267.9≈268(天)
这些组中值的方差为
[1×(165-268)2+11×(195-268)2+18×(225-268)2+20×(255-268)2+25×(285-268)2+16× (315-268)2+7×(345-268)2+2×(375-268)2] ÷100=2128.60(天2).
故所求的标准差约 (天)
答:估计这种日光灯的平均使用寿命约为268天,标准差约为46天.
2.2.2 用样本的数字特征估计总体的数字特征(二)
二、用样本的标准差估计总体的标准差
数据的离散程度可以用极差、方差或标准差来描述。
为了表示样本数据的单位表示的波动幅度,通常要求出样本方差或者它的算术平方根.
(1)方差:设在一组数据,x1,x2,…,xn中,各数据与它们的平均数x的差的平方分别是
来衡量这组数据的波动大小,并把它叫做这组数据的方差,一组数据方差越大,则这组数据波动越大。
那么我们用它们的平均数,即
(2)标准差:我们把数据的方差的算术平方根叫做这组数据的标准差,它也是一个用来衡量一组数据的波动大小的重要的量。
计算标准差的算法:
S2 算出每个样本数据与样本平均数的差
(i=1,2,……,n);
S1 算出样本数据的平均数x;
S3 算出 (i=1,2,…,n);
S4 算出 (i=1,2,…,n)这n个数的平均数,即为样本方差s2;
S5 算出方差的算术平方根,即为样本标准差s。
例1. 计算数据5,7,7,8,10,11的标准差.
解:S1 x= ——————— =8
5+7+7+8+10+11
6
数据 xi S1 x S2 xi-x S3 (xi-x)2
5 8 -3 9
7 8 -1 1
7 8 -1 1
8 8 0 0
10 8 2 4
11 8 3 9
S4 s2= ——————— =4;
9+1+1+0+4+9
6
S5 .
所以这组数据的标准差是2.
例2. 从某灯泡厂生产的一批灯泡中随机地抽取10只进行寿命测试,得数据如下(单位:h):
1458,1395,1562,1614,1351,1490,1478,1382,1536,1496
使用函数型计算器或计算机的Excel软件求样本的平均数x和样本的标准差。
解:按键
MODE
2 (进入统计计算状态)
将计算器存储器设置成初始状态
SHIFT
Scl
=
1458 1395 1562 1614 1351 1490 1478 1382 1536 1496
DT
DT
DT
DT
DT
DT
DT
DT
DT
DT
继续按下表按键
按键 显示结果
1476.2
78.7309342
SHIFT
SHIFT
xσn
=
=
x
解2:打开Excel工作表,在一列输入数据,如将10个数据输入A1到A10单元格中.
(1)利用求和∑计算它们的和;
(2)用函数AVERAGE(A1:A10)求它们的平均数;
(3)用函数VARPA(A1:A10)求它们的方差;
(4)用开方函数Sqrt(方差)计算它们的标准差.
例3.计算数据89,93,88,91,94,90,88,87的方差和标准差。(标准差结果精确到0.1)
解:
.
所以这组数据的方差为5.5,标准差为2.3 .
例4. 从甲、乙两名学生中选拔一人乘积射击比赛,对他们的射击水平进行测试,两人在相同的条件下各射击10次,命中环数如下﹕
甲﹕7,8,6,8,6,5,8,10,7,4;
乙﹕9,5,7,8,7,6,8,6,7,7.
(1)计算甲、乙两人射击命中环数的平均数和标准差;
(2)比较两人的成绩,然后决定选择哪一人参赛.
解:(1)计算得x甲=7,x乙=7;
s甲=1.73,s乙=1.10.
(2)由(1)知,甲、乙两人平均成绩相等,但s乙
从标准差的定义可知,如果样本各数据都相等,则标准差得0,这表明数据没有波动幅度,数据没有离散性;若个体的值与平均数的差的绝对值较大,则标准差也较大,表明数据的波动幅度也很大,数据的离散程度很高,因此标准差描述了数据对平均数的离散程度。
A B
样本数据 3 3 3 3 3 1 1 3 5 5
平均数 3 3
标准差 0 1.79
频率分布直方图
数据没有离散度
数据离散程度很高
再看钢管内径尺寸的例子,它的样本平均数是25.401,样本标准差是0.056,再直方图中用虚线标出平均数所在的位置,并画出距平均数两侧各一倍标准差和两倍标准差的区间。可以看到大约有70%的钢管内径尺寸落在距平均数两侧各一倍标准差的区间内,即(x-s, x+s)
大约有95%的钢管内径尺寸落在距平均数两侧各两倍标准差的区间内,即(x-2s, x+2s)。
s
s
2s
2s
x
的平均数为 ,
(2)新数据
方差为 .
,方差仍为 .
(1)新数据
的平均数为
,方差为 .
的平均数为
(3)新数据
如果数据
的平均数为 ,
方差为
,则
(4)方差的运算性质:
练习:
(3)若k1,k2,…, k8的方差为3,则2(k1-3),
2(k2-3), …, 2(k8-3)的方差为________
4
32
12
A
B
(7)在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为________
9.5,0.016
五、回顾小结:
1.用样本的数字特征估计总体的数字特征分两类:
用样本平均数估计总体平均数。
用样本方差、标准差估计总体方差、标准差。样本容量越大,估计就越精确。
2.方差、标准差描述一组数据围绕平均数波动的大小,反映了一组数据变化的幅度.
1.甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:t/hm2),试根据这组数据估计哪一种水稻品种的产量比较稳定。
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
解:甲品种的样本平均数为10,样本方差为 [(9.8-10)2 +(9.9-10)2+(10.1-10)2+ (10-10)2+(10.2-10)2]÷5=0.02.
乙品种的样本平均数也为10,样本方差为 [(9.4-10)2+(10.3-10)2+(10.8-10)2+ (9.7-10)2+(9.8-10)2]÷5=0.24.
因为0.24>0.02,
所以,由这组数据可以认为甲种水稻的产量比较稳定。
2.为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换。已知某校使用的100只日光灯在必须换掉前的使用天数如下,试估计这种日光灯的平均使用寿命和标准差。
天数 151~180 181~210 211~240 241~270 271~300 301~330 331~360 361~390
灯泡数 1 11 18 20 25 16 7 2
解:各组中值分别为165,195,225,285,315,345,375,由此算得平均数约为
165×1%+195×11%+225×18%+255×20%+285×25%+315×16%+345×7%+375×2%=267.9≈268(天)
这些组中值的方差为
[1×(165-268)2+11×(195-268)2+18×(225-268)2+20×(255-268)2+25×(285-268)2+16× (315-268)2+7×(345-268)2+2×(375-268)2] ÷100=2128.60(天2).
故所求的标准差约 (天)
答:估计这种日光灯的平均使用寿命约为268天,标准差约为46天.
