【数学】2.3.1《变量间的相互关系》课件(新人教b版必修3)
文档属性
| 名称 | 【数学】2.3.1《变量间的相互关系》课件(新人教b版必修3) |

|
|
| 格式 | rar | ||
| 文件大小 | 17.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 17:18:32 | ||
图片预览





文档简介
(共17张PPT)
2.3.1 变量间的相互关系(一)
一、变量之间的相关关系
变量与变量之间的关系常见的有两类:一类是确定性的函数关系,像正方形的边长a和面积S的关系,另一类是变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有随机性的。
例如,由人的身高并不能确定体重,但一般说来“身高者,体也重”,我们说身高与体重这两个变量具有相关关系.
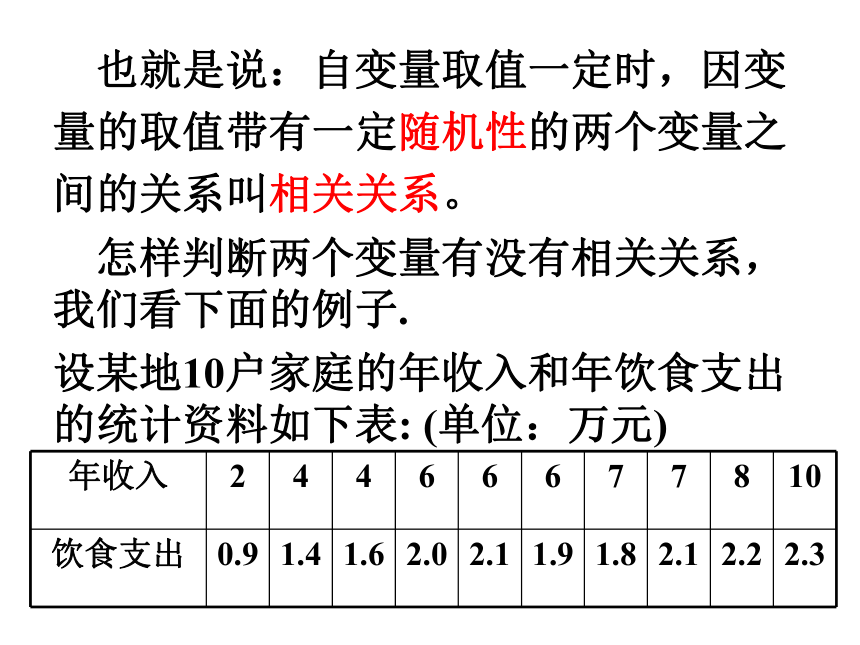
也就是说:自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫相关关系。
怎样判断两个变量有没有相关关系,我们看下面的例子.
设某地10户家庭的年收入和年饮食支出的统计资料如下表: (单位:万元)
年收入 2 4 4 6 6 6 7 7 8 10
饮食支出 0.9 1.4 1.6 2.0 2.1 1.9 1.8 2.1 2.2 2.3
由表中数据可以看出,y有随x增加而增加的趋势,并且增加的趋势变缓。
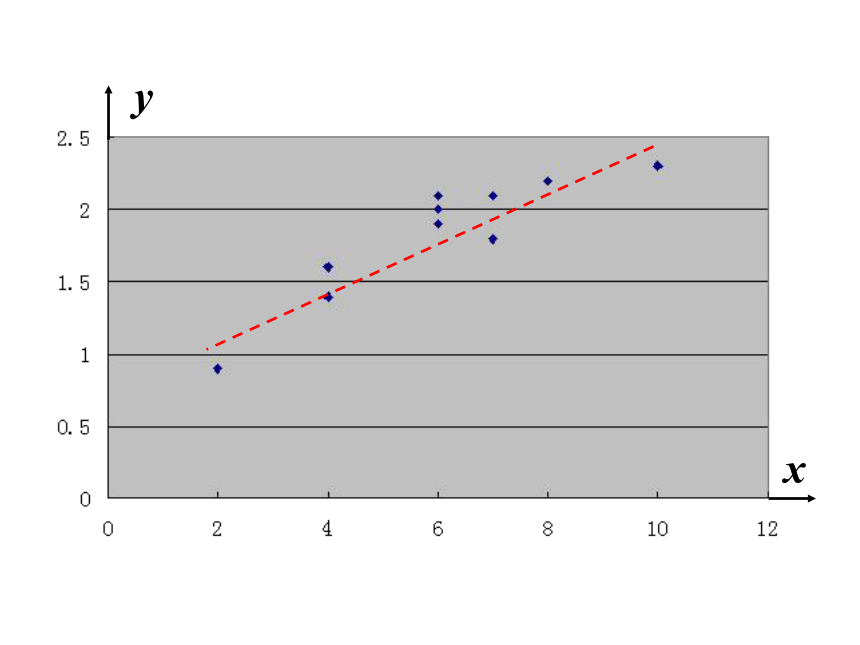
为了更清楚地看出x与y是否有相关关系,我们以年收入x的取值为横坐标,把年饮食支出y的相应取值作为纵坐标,在直角坐标系中描点。这样的图形叫做散点图。
x
y
从图中可以看出家庭年收入和年饮食支出之间具有相关关系。
并且当年收入的值由小变大时,年饮食支出的值也在由小变大。这种相关称作正相关;反之如果一个变量的值由小变大时,另一个变量的值由大变小,这种相关称作负相关。
相关关系与函数关系的异同点
(1)相同点:两者均是指两个变量的关系;
(2)不同点:函数关系是一种确定的关系,如匀速直线运动中时间t与路程s的关系;
相关关系是一种非确定的关系,如一块农田的水稻产量与施肥量之间的关系,事实上,函数关系是两个非随机变量的关系,而相关关系是非随机变量与随机变量的关系。
函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系。
例如,有人发现,对于在校儿童,鞋的大小与阅读能力有很强的相关关系,然而学会新词并不能使脚变大,而是涉及到第三个因素——年龄,当儿童长大一些以后,他的阅读能力会提高,而且由于人长大脚也变大。
如何分析变量之间是否具有相关的关系
分析变量之间是否具有相关的关系,我们可以借助日常生活和工作经验对一些常规问题来进行定性分析,如儿童的身高随着年龄的增长而增长,但它们之间又不存在一种确定的函数关系,因此它们之间是一种非确定性的随机关系,即相关关系。但仅凭这种定性分析不够;
一来定性分析有时会给我们以误导; 二来定性分析无法确定变量之间相互影响的程度有多大。因些,我们还需要进行定量分析。
如何进行定量分析呢?由于变量间的相关关系是一种随机关系,因此,我们只能借助统计这一工具来解决问题,也就是通过收集大量数据,在对数据进行统计分析的基础上,发现其中的规律,并对它们之间的关系作出推断。
两个变量之间的相关关系有哪些?
从散点图上可以看出,如果变量之间存在着某种关系,这些点会有一个集中的大致趋势,这种趋势通常可以用一条光滑的曲线来近似描述,这种近似的过程称为曲线拟合。在两个变量x和y的散点图中,所有点看上去都在一条直线附近波动,则称变量间是线性相关的。此时,我们可以用一条直线来拟合(如图),这条直线叫回归直线。
例2. 5个学生的数学和物理成绩如下表:
学生
学科 A B C D E
数学 80 75 70 65 60
物理 70 66 68 64 62
画出散点图,并判断它们是否有相关关系.
数学
物理
具有相关关系.
例3. 下表给出了某校12名高一学生的身高(单位:cm)和体重(单位:kg):
身高 151 152 153 154 156 157 158 160 160 162 163 164
体重 40 41 41 41.5 42 42.5 43 44 45 45 46 45.5
画出散点图,并观察它们是否有相关关系.
身高
体重
具有相关关系.
例4. 某农场经过观测得到水稻产量和施化肥量的统计数据如下:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
画出的散点图 ,判断它们是否有相关关系,并考虑水稻的产量会不会随化肥使用量的增加而一直增长。
x
y
散点图如下:具有相关关系.
水稻的产量不会随化肥使用量的增加而一直增长。
2.3.1 变量间的相互关系(一)
一、变量之间的相关关系
变量与变量之间的关系常见的有两类:一类是确定性的函数关系,像正方形的边长a和面积S的关系,另一类是变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有随机性的。
例如,由人的身高并不能确定体重,但一般说来“身高者,体也重”,我们说身高与体重这两个变量具有相关关系.
也就是说:自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫相关关系。
怎样判断两个变量有没有相关关系,我们看下面的例子.
设某地10户家庭的年收入和年饮食支出的统计资料如下表: (单位:万元)
年收入 2 4 4 6 6 6 7 7 8 10
饮食支出 0.9 1.4 1.6 2.0 2.1 1.9 1.8 2.1 2.2 2.3
由表中数据可以看出,y有随x增加而增加的趋势,并且增加的趋势变缓。
为了更清楚地看出x与y是否有相关关系,我们以年收入x的取值为横坐标,把年饮食支出y的相应取值作为纵坐标,在直角坐标系中描点。这样的图形叫做散点图。
x
y
从图中可以看出家庭年收入和年饮食支出之间具有相关关系。
并且当年收入的值由小变大时,年饮食支出的值也在由小变大。这种相关称作正相关;反之如果一个变量的值由小变大时,另一个变量的值由大变小,这种相关称作负相关。
相关关系与函数关系的异同点
(1)相同点:两者均是指两个变量的关系;
(2)不同点:函数关系是一种确定的关系,如匀速直线运动中时间t与路程s的关系;
相关关系是一种非确定的关系,如一块农田的水稻产量与施肥量之间的关系,事实上,函数关系是两个非随机变量的关系,而相关关系是非随机变量与随机变量的关系。
函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系。
例如,有人发现,对于在校儿童,鞋的大小与阅读能力有很强的相关关系,然而学会新词并不能使脚变大,而是涉及到第三个因素——年龄,当儿童长大一些以后,他的阅读能力会提高,而且由于人长大脚也变大。
如何分析变量之间是否具有相关的关系
分析变量之间是否具有相关的关系,我们可以借助日常生活和工作经验对一些常规问题来进行定性分析,如儿童的身高随着年龄的增长而增长,但它们之间又不存在一种确定的函数关系,因此它们之间是一种非确定性的随机关系,即相关关系。但仅凭这种定性分析不够;
一来定性分析有时会给我们以误导; 二来定性分析无法确定变量之间相互影响的程度有多大。因些,我们还需要进行定量分析。
如何进行定量分析呢?由于变量间的相关关系是一种随机关系,因此,我们只能借助统计这一工具来解决问题,也就是通过收集大量数据,在对数据进行统计分析的基础上,发现其中的规律,并对它们之间的关系作出推断。
两个变量之间的相关关系有哪些?
从散点图上可以看出,如果变量之间存在着某种关系,这些点会有一个集中的大致趋势,这种趋势通常可以用一条光滑的曲线来近似描述,这种近似的过程称为曲线拟合。在两个变量x和y的散点图中,所有点看上去都在一条直线附近波动,则称变量间是线性相关的。此时,我们可以用一条直线来拟合(如图),这条直线叫回归直线。
例2. 5个学生的数学和物理成绩如下表:
学生
学科 A B C D E
数学 80 75 70 65 60
物理 70 66 68 64 62
画出散点图,并判断它们是否有相关关系.
数学
物理
具有相关关系.
例3. 下表给出了某校12名高一学生的身高(单位:cm)和体重(单位:kg):
身高 151 152 153 154 156 157 158 160 160 162 163 164
体重 40 41 41 41.5 42 42.5 43 44 45 45 46 45.5
画出散点图,并观察它们是否有相关关系.
身高
体重
具有相关关系.
例4. 某农场经过观测得到水稻产量和施化肥量的统计数据如下:
施化肥量x 15 20 25 30 35 40 45
水稻产量y 330 345 365 405 445 450 455
画出的散点图 ,判断它们是否有相关关系,并考虑水稻的产量会不会随化肥使用量的增加而一直增长。
x
y
散点图如下:具有相关关系.
水稻的产量不会随化肥使用量的增加而一直增长。
