青岛版数学八年级上册课件1.2怎样判定三角形全等课件(第1课时SAS)(共21张PPT)
文档属性
| 名称 | 青岛版数学八年级上册课件1.2怎样判定三角形全等课件(第1课时SAS)(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 956.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-11 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第1章
全等三角形
1.2怎样判定三角形全等
第1课时
教学目标
1.知道三角形全等“边角边”的内容;
2.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件;
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。
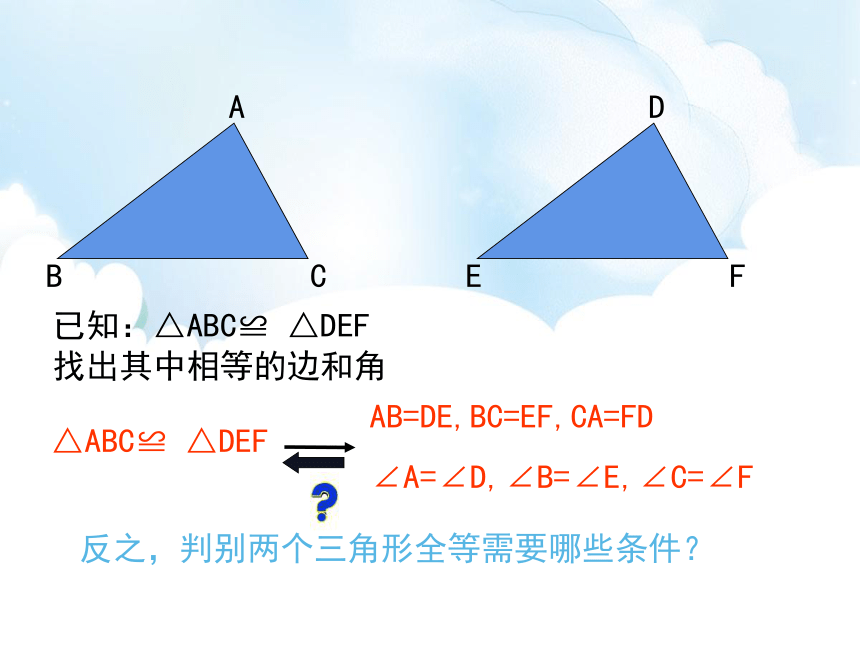
已知:△ABC≌
△DEF
找出其中相等的边和角
反之,判别两个三角形全等需要哪些条件?
AB=DE,BC=EF,CA=FD
∠A=∠D,∠B=∠E,∠C=∠F
△ABC≌
△DEF
一个条件
寻求判别三角形全等的条件
三个条件
边边边
角角角
两角一边
两边一角
两个条件
全等三角形:三组边对应相等,三对角对应相等
一组边相等
一对角相等
两边和它的夹角
两边和它一边的对角
两角和它的夹边
两角和一角的对边
一边一角相等
两对角相等
两组边相等
只给一个条件(一条边或一个角)
只给一条边时,如:
3cm
3cm
3cm
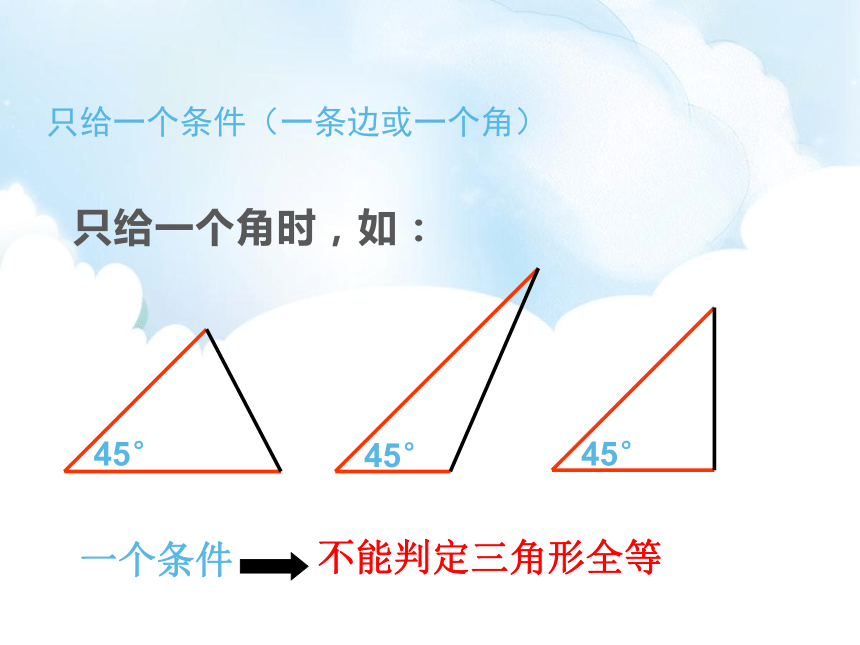
只给一个角时,如:
45°
45°
45°
只给一个条件(一条边或一个角)
一个条件
不能判定三角形全等
给出两个条件时(一边及一角)
如果三角形的一条边为3cm,一个内角为30°
3cm
3cm
3cm
30°
30°
30°
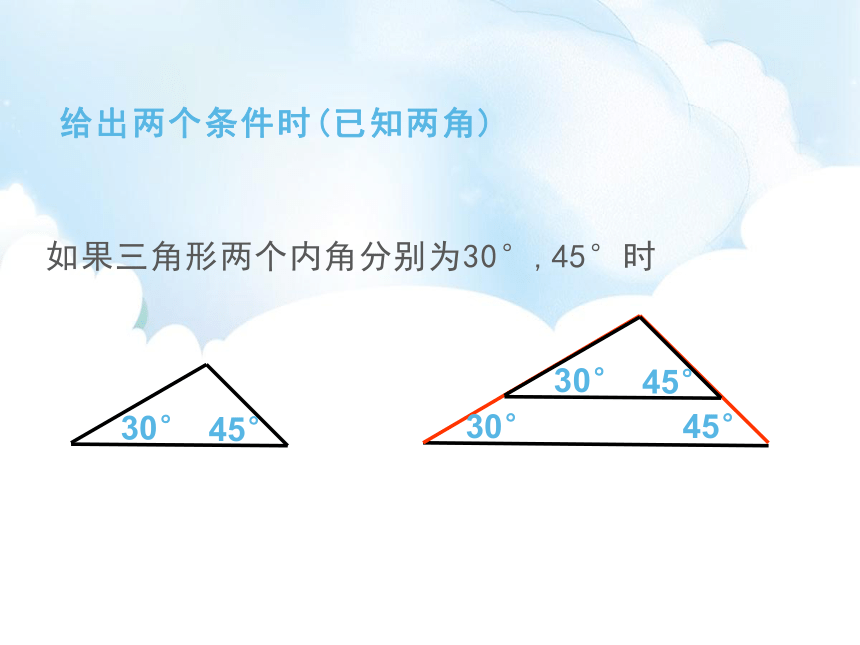
给出两个条件时(已知两角)
如果三角形两个内角分别为30°,45°时
30°
45°
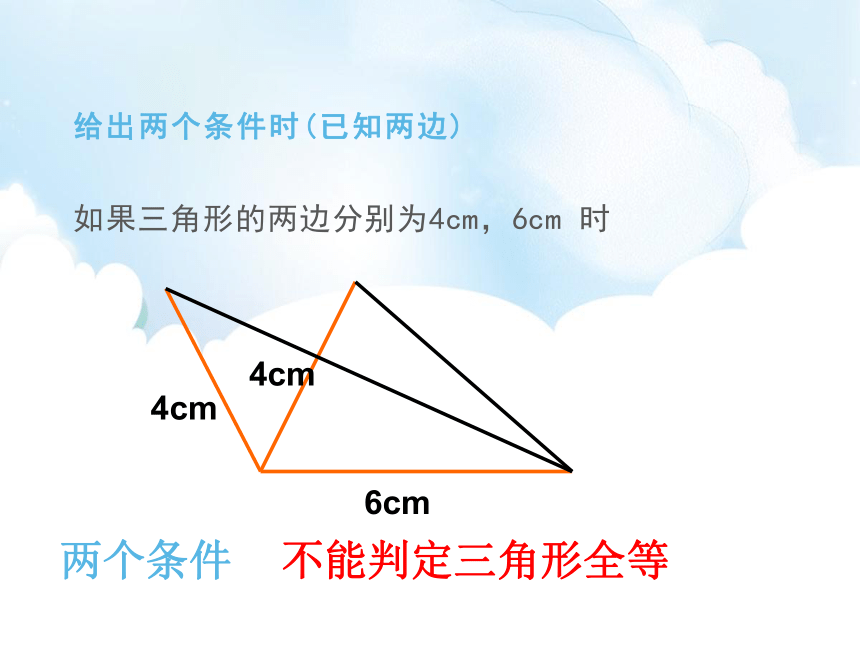
给出两个条件时(已知两边)
如果三角形的两边分别为4cm,6cm
时
6cm
4cm
4cm
两个条件
不能判定三角形全等
两边一角对应相等
两边夹角对应相等
(边角边)
两边一对角对应相等
(边边角)
给出三个条件时(已知两边一角)
大家一起做下面的实验:
1、用三角板画∠MAN=45°;
2、在AM上截取AB=3cm;在AN上截取AC=2cm;
3、连接BC。
与周围同学所剪的比较一下,它们全等吗?
你得出什么结论?
B
C
′
\
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
在△ABC和△DEF中,
AB=DE
∠B=∠E
BC=EF
∴
△ABC≌△DEF
(SAS)
若两个三角形两边以及这两边的夹角对应相等
则这两个三角形全等
条件:AB=DE,∠B=∠E,
BC=EF
结论:
△ABC≌△DEF
判定方法1
两边及其夹角分别相等的两个三角形全等.
可以简写成
“边角边”
或“
SAS
”
用数学语言表述:
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SAS)
AB=DE
∠A=∠D
CA=FD
新知学习
练一练1:
在下列三角形中,哪两个三角形全等?
⑴
⑵
⑶
⑷
⑸
⑹
解:全等的三角形有:⑴和⑷,
⑶和⑸.
已知:如图,
AB=AD
,∠BAC=
∠DAC
△ABC
和△ADC
全等吗?
分析:
△
ABC
≌△
ADC
AB=AD(已知)
∠BAC=∠DAC
(已知)
?
B
C
D
A
AC=AC(公共边)
例1
1.
如图,AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
注意:
要充分利用图形中“对顶角相等”这个条件.
练一练:
2、如图:AB=AC,AD=AE,△ABE和△ACD全等吗?请说明理由。
注意:
要充分利用图形中“公共角”这个条件.
你还能得到哪些相等的线段?说明理由.
两边以及其中一边的对角对应相等的两个三角形全等吗?
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,
你发现了什么?
做一做
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其中一边所对的角对应相等,两个三角形不一定全等.
先画一个40°的角,然后在其中一边上取3.5厘米,最后画40°的角所对的边2.5厘米.
某校八年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长AC至D,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?
C
·
A
D
E
B
实际应用
小结:
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
两边以及其中一边的对角对应相等的两个三角形不一定全等.
判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
三角形全等书写三步骤:
(1)写出在哪两个三角形中
(2)摆出三个条件用大括号括起来
(3)写出全等结论
第1章
全等三角形
1.2怎样判定三角形全等
第1课时
教学目标
1.知道三角形全等“边角边”的内容;
2.会运用“SAS”识别三角形全等,为证明线段相等或角相等创造条件;
3.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。
已知:△ABC≌
△DEF
找出其中相等的边和角
反之,判别两个三角形全等需要哪些条件?
AB=DE,BC=EF,CA=FD
∠A=∠D,∠B=∠E,∠C=∠F
△ABC≌
△DEF
一个条件
寻求判别三角形全等的条件
三个条件
边边边
角角角
两角一边
两边一角
两个条件
全等三角形:三组边对应相等,三对角对应相等
一组边相等
一对角相等
两边和它的夹角
两边和它一边的对角
两角和它的夹边
两角和一角的对边
一边一角相等
两对角相等
两组边相等
只给一个条件(一条边或一个角)
只给一条边时,如:
3cm
3cm
3cm
只给一个角时,如:
45°
45°
45°
只给一个条件(一条边或一个角)
一个条件
不能判定三角形全等
给出两个条件时(一边及一角)
如果三角形的一条边为3cm,一个内角为30°
3cm
3cm
3cm
30°
30°
30°
给出两个条件时(已知两角)
如果三角形两个内角分别为30°,45°时
30°
45°
给出两个条件时(已知两边)
如果三角形的两边分别为4cm,6cm
时
6cm
4cm
4cm
两个条件
不能判定三角形全等
两边一角对应相等
两边夹角对应相等
(边角边)
两边一对角对应相等
(边边角)
给出三个条件时(已知两边一角)
大家一起做下面的实验:
1、用三角板画∠MAN=45°;
2、在AM上截取AB=3cm;在AN上截取AC=2cm;
3、连接BC。
与周围同学所剪的比较一下,它们全等吗?
你得出什么结论?
B
C
′
\
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
在△ABC和△DEF中,
AB=DE
∠B=∠E
BC=EF
∴
△ABC≌△DEF
(SAS)
若两个三角形两边以及这两边的夹角对应相等
则这两个三角形全等
条件:AB=DE,∠B=∠E,
BC=EF
结论:
△ABC≌△DEF
判定方法1
两边及其夹角分别相等的两个三角形全等.
可以简写成
“边角边”
或“
SAS
”
用数学语言表述:
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SAS)
AB=DE
∠A=∠D
CA=FD
新知学习
练一练1:
在下列三角形中,哪两个三角形全等?
⑴
⑵
⑶
⑷
⑸
⑹
解:全等的三角形有:⑴和⑷,
⑶和⑸.
已知:如图,
AB=AD
,∠BAC=
∠DAC
△ABC
和△ADC
全等吗?
分析:
△
ABC
≌△
ADC
AB=AD(已知)
∠BAC=∠DAC
(已知)
?
B
C
D
A
AC=AC(公共边)
例1
1.
如图,AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。
注意:
要充分利用图形中“对顶角相等”这个条件.
练一练:
2、如图:AB=AC,AD=AE,△ABE和△ACD全等吗?请说明理由。
注意:
要充分利用图形中“公共角”这个条件.
你还能得到哪些相等的线段?说明理由.
两边以及其中一边的对角对应相等的两个三角形全等吗?
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,
你发现了什么?
做一做
A
B
C
D
E
F
2.5cm
3.5cm
40°
40°
3.5cm
2.5cm
结论:两边及其中一边所对的角对应相等,两个三角形不一定全等.
先画一个40°的角,然后在其中一边上取3.5厘米,最后画40°的角所对的边2.5厘米.
某校八年级一班学生到野外活动,为测量一池塘两端A、B的距离。设计了如下方案:如图,先在平地上取一个可直接到达A、B的点C,再连结AC、BC并分别延长AC至D,使DC=AC,EC=BC,最后测得DE的距离即为AB的长.你认为这种方法是否可行?
C
·
A
D
E
B
实际应用
小结:
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
两边以及其中一边的对角对应相等的两个三角形不一定全等.
判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
三角形全等书写三步骤:
(1)写出在哪两个三角形中
(2)摆出三个条件用大括号括起来
(3)写出全等结论
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
