【数学】2.3.2《两个变量的线性相关》课件(新人教b版必修3)
文档属性
| 名称 | 【数学】2.3.2《两个变量的线性相关》课件(新人教b版必修3) |

|
|
| 格式 | rar | ||
| 文件大小 | 647.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
2.3.2 两个变量的线性相关
.
求和符号
如:
记为:
复习引入:
1、现实生活中存在许多相关关系:商品销售与广告、粮食生产与施肥量、人体的脂肪量与年龄等等的相关关系.
2、通过收集大量的数据,进行统计,对数据分析,找出其中的规律,对其相关关系作出一定判断.
3、由于变量之间相关关系的广泛性和不确定性,所以样本数据应较大,和有代表性.才能对它们之间的关系作出正确的判断.
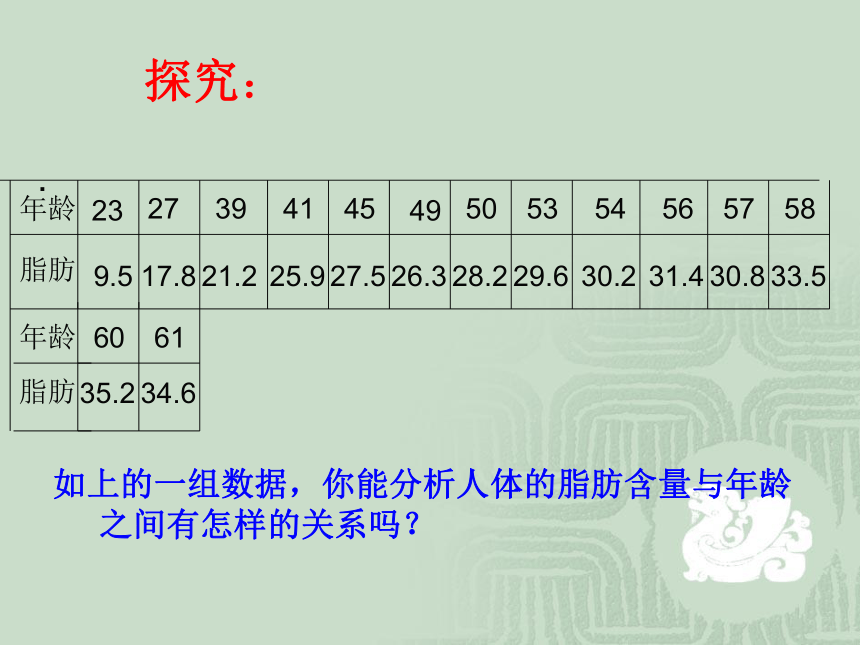
探究:
.
年龄
脂肪
23
9.5
27
17.8
39
21.2
41
25.9
45
49
27.5
26.3
50
28.2
53
29.6
54
30.2
56
31.4
57
30.8
年龄
脂肪
58
33.5
60
35.2
61
34.6
如上的一组数据,你能分析人体的脂肪含量与年龄
之间有怎样的关系吗?
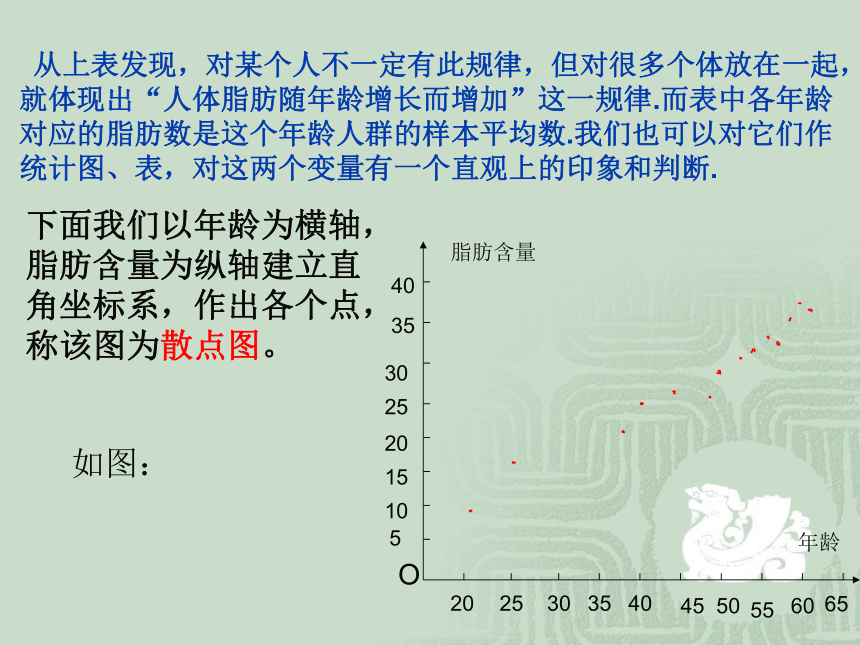
从上表发现,对某个人不一定有此规律,但对很多个体放在一起,就体现出“人体脂肪随年龄增长而增加”这一规律.而表中各年龄对应的脂肪数是这个年龄人群的样本平均数.我们也可以对它们作统计图、表,对这两个变量有一个直观上的印象和判断.
下面我们以年龄为横轴,
脂肪含量为纵轴建立直
角坐标系,作出各个点,
称该图为散点图。
如图:
O
20
25
30
35
40
45
50
55
60
65
年龄
脂肪含量
5
10
15
20
25
30
35
40
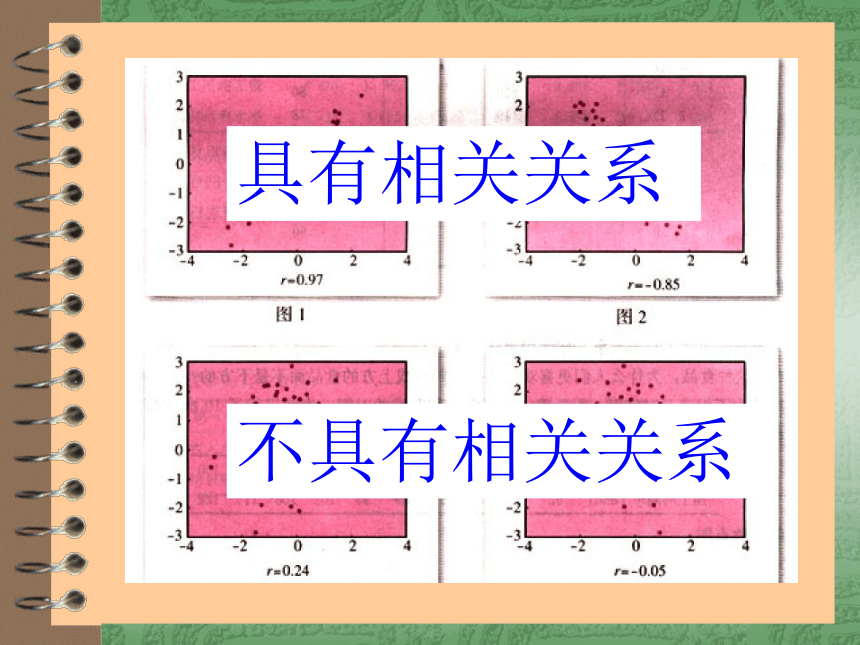
具有相关关系
不具有相关关系
从刚才的散点图发现:年龄越大,体内脂肪含量越高,点的位置散布在从左下角到右上角的区域。称它们成正相关。但有的两个变量的相关,如下图所示:
如高原含氧量与海拔高度
的相关关系,海平面以上,
海拔高度越高,含氧量越
少。
作出散点图发现,它们散
布在从左上角到右下角的区
域内。又如汽车的载重和汽
车每消耗1升汽油所行使的
平均路程,称它们成负相关.
O
我们再观察它的图像发现这些点大致分布在一条直线附
近,像这样,如果散点图中点的分布从整体上看大致在
一条直线附近,我们就称这两个变量之间具有线性相
关关系,这条直线叫做回归直线,该直线叫回归直线方程。
20
25
30
35
40
45
50
55
60
65
年龄
脂肪含量
0
5
10
15
20
25
30
35
40
用方程
在一般统计书中习惯用b表示一次项系数,用a表示常数项,这正好与我们表示的一次函数习惯相反.
离差:
将
称为离差.
叫总离差
最小二乘法:
为最小的方法.
2
求
利用配方法求得:
例1:观察两相关变量得如下表:
x -1 -2 -3 -4 -5 5 3 4 2 1
y -9 -7 -5 -3 -1 1 5 3 7 9
求两变量间的回归方程
解:
列表:
i 1 2 3 4 5 6 7 8 9 10
-1 -2 -3 -4 -5 5 3 4 2 1
-9 -7 -5 -3 -1 1 5 3 7 9
9 14 15 12 5 5 15 12 14 9
计算得:
∴所求回归直线方程为 y=x
^
小结:求线性回归直线方程的步骤:
第一步:列表 ;
第二步:计算 ;
第三步:代入公式计算b,a的值;
第四步:写出直线方程。
例2:有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度 -5 0 4 7 12 15 19 23 27 31 36
热饮杯数 156 150 132 128 130 116 104 89 93 76 54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一
般规律;
(3)求回归方程;
(4)如果某天的气温是 C,预测这天卖出的热饮杯数。
解: (1)散点图
(2)气温与热饮杯数成负相关,即气温越高, 卖出去的热饮杯数越少。
温度
热饮杯数
(3)从散点图可以看出,这些点大致分布在一条直线附近。
y=-2.352x+147.767
^
(4)当x=2时,y=143.063,因此,这天大约可以卖出143杯热饮。
^
(3)
=-2.352
=143.767
2.3.2 两个变量的线性相关
.
求和符号
如:
记为:
复习引入:
1、现实生活中存在许多相关关系:商品销售与广告、粮食生产与施肥量、人体的脂肪量与年龄等等的相关关系.
2、通过收集大量的数据,进行统计,对数据分析,找出其中的规律,对其相关关系作出一定判断.
3、由于变量之间相关关系的广泛性和不确定性,所以样本数据应较大,和有代表性.才能对它们之间的关系作出正确的判断.
探究:
.
年龄
脂肪
23
9.5
27
17.8
39
21.2
41
25.9
45
49
27.5
26.3
50
28.2
53
29.6
54
30.2
56
31.4
57
30.8
年龄
脂肪
58
33.5
60
35.2
61
34.6
如上的一组数据,你能分析人体的脂肪含量与年龄
之间有怎样的关系吗?
从上表发现,对某个人不一定有此规律,但对很多个体放在一起,就体现出“人体脂肪随年龄增长而增加”这一规律.而表中各年龄对应的脂肪数是这个年龄人群的样本平均数.我们也可以对它们作统计图、表,对这两个变量有一个直观上的印象和判断.
下面我们以年龄为横轴,
脂肪含量为纵轴建立直
角坐标系,作出各个点,
称该图为散点图。
如图:
O
20
25
30
35
40
45
50
55
60
65
年龄
脂肪含量
5
10
15
20
25
30
35
40
具有相关关系
不具有相关关系
从刚才的散点图发现:年龄越大,体内脂肪含量越高,点的位置散布在从左下角到右上角的区域。称它们成正相关。但有的两个变量的相关,如下图所示:
如高原含氧量与海拔高度
的相关关系,海平面以上,
海拔高度越高,含氧量越
少。
作出散点图发现,它们散
布在从左上角到右下角的区
域内。又如汽车的载重和汽
车每消耗1升汽油所行使的
平均路程,称它们成负相关.
O
我们再观察它的图像发现这些点大致分布在一条直线附
近,像这样,如果散点图中点的分布从整体上看大致在
一条直线附近,我们就称这两个变量之间具有线性相
关关系,这条直线叫做回归直线,该直线叫回归直线方程。
20
25
30
35
40
45
50
55
60
65
年龄
脂肪含量
0
5
10
15
20
25
30
35
40
用方程
在一般统计书中习惯用b表示一次项系数,用a表示常数项,这正好与我们表示的一次函数习惯相反.
离差:
将
称为离差.
叫总离差
最小二乘法:
为最小的方法.
2
求
利用配方法求得:
例1:观察两相关变量得如下表:
x -1 -2 -3 -4 -5 5 3 4 2 1
y -9 -7 -5 -3 -1 1 5 3 7 9
求两变量间的回归方程
解:
列表:
i 1 2 3 4 5 6 7 8 9 10
-1 -2 -3 -4 -5 5 3 4 2 1
-9 -7 -5 -3 -1 1 5 3 7 9
9 14 15 12 5 5 15 12 14 9
计算得:
∴所求回归直线方程为 y=x
^
小结:求线性回归直线方程的步骤:
第一步:列表 ;
第二步:计算 ;
第三步:代入公式计算b,a的值;
第四步:写出直线方程。
例2:有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度 -5 0 4 7 12 15 19 23 27 31 36
热饮杯数 156 150 132 128 130 116 104 89 93 76 54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一
般规律;
(3)求回归方程;
(4)如果某天的气温是 C,预测这天卖出的热饮杯数。
解: (1)散点图
(2)气温与热饮杯数成负相关,即气温越高, 卖出去的热饮杯数越少。
温度
热饮杯数
(3)从散点图可以看出,这些点大致分布在一条直线附近。
y=-2.352x+147.767
^
(4)当x=2时,y=143.063,因此,这天大约可以卖出143杯热饮。
^
(3)
=-2.352
=143.767
