【数学】3.1.4《概率的加法公式》课件(新人教b版必修3)
文档属性
| 名称 | 【数学】3.1.4《概率的加法公式》课件(新人教b版必修3) |  | |
| 格式 | rar | ||
| 文件大小 | 43.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-19 17:18:32 | ||
图片预览











文档简介
(共32张PPT)
3.1.4 概率的加法公式
一、互斥事件、事件的并、对立事件
1.互斥事件:不可能同时发生的两个事件叫做互斥事件(或称为互不相容事件);
2.事件的并:由事件A和B至少有一个发生(即A发生,或B发生,或A、B都发生)所构成的事件C,称为事件A与B的并(或和)。记作C=A∪B(或C=A+B)。
事件A∪B是由事件A或B所包含的基本事件所组成的集合。
3.对立事件:不能同时发生且必有一个发生的两个事件叫做互为对立事件。
事件A的对立事件记作.
例1. 抛掷一颗骰子,观察掷出的点数. 设事件A为“出现奇数点”,B为“出现2点”. 已知P(A)= ,P(B)= ,求“出现奇数点或2点”的概率。
这里的事件A和事件B不可能同时发生,这种不可能同时发生的两个事件叫做互斥事件
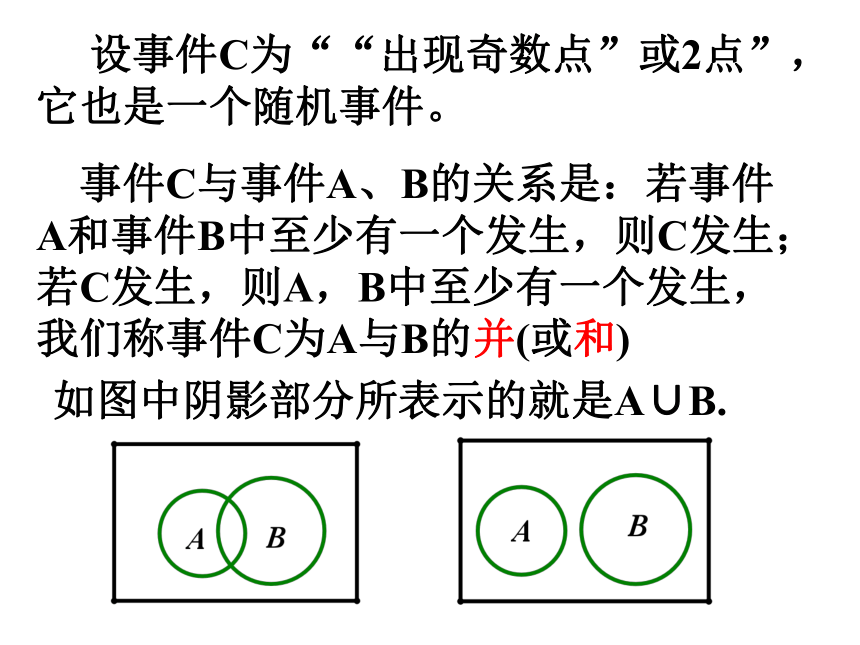
设事件C为““出现奇数点”或2点”,它也是一个随机事件。
事件C与事件A、B的关系是:若事件A和事件B中至少有一个发生,则C发生;若C发生,则A,B中至少有一个发生,我们称事件C为A与B的并(或和)
设事件C为““出现奇数点”或2点”,它也是一个随机事件。
事件C与事件A、B的关系是:若事件A和事件B中至少有一个发生,则C发生;若C发生,则A,B中至少有一个发生,我们称事件C为A与B的并(或和)
如图中阴影部分所表示的就是A∪B.
例2.判断下列各对事件是否是互斥事件,并说明理由。
某小组有3名男生和2名女生,从中任选2名同学去参加演讲比赛,其中
(1)恰有1名男生和恰有2名男生;
(2)至少有1名男生和至少有1名女生;
(3)至少有1名男生和全是男生;
(4)至少有1名男生和全是女生。
解:(1)是互斥事件;
(2)不可能是互斥事件;
(3)不可能是互斥事件;
(4)是互斥事件;
例3.判断下列给出的每对事件,(1)是否为互斥事件,(2)是否为对立事件,并说明理由。
从40张扑克牌(红桃、黑桃、方块、梅花,点数从1~10各4张)中,任取1张:
(1)“抽出红桃”与“抽出黑桃”;
(2)“抽出红色牌”与“抽出黑色牌”;
(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”。
解:(1)是互斥事件,不是对立事件;
(2)既是互斥事件,又是对立事件;
(3)不是互斥事件,当然不可能是对立事件;
所以对立事件一定是互斥事件,而互斥事件不一定是对立事件。
假定事件A与B互斥,则
P(A∪B)=P(A)+P(B)。
二、互斥事件的概率加法公式
证明:假定A、B为互斥事件,在n次试验中,事件A出现的频数为n1,事件B出现的频数为n2,则事件A∪B出现的频数正好是n1+n2,所以事件A∪B的频率为
如果用μn(A)表示在n次试验中事件A出现的频率,则有μn(A∪B)=μn(A)+μn(B).
由概率的统计定义可知,
P(A∪B)=P(A)+P(B)。
一般地,如果事件A1,A2,…,An彼此互斥,那么P(A1∪A2∪…∪An)=P(A1)+P(A2) +…+P(An),即彼此互斥事件和的概率等于概率的和.
在求某些较为复杂事件的概率时,先将它分解为一些较为简单的、并且概率已知(或较容易求出)的彼此互斥的事件,然后利用概率的加法公式求出概率. 因此互斥事件的概率加法公式具有“化整为零、化难为易”的功效,但需要注意的是使用该公式时必须检验是否满足它的前提条件“彼此互斥”.
例1中事件C:“出现奇数点或2点”的概率是事件A:“出现奇数点”的概率与事件B:“出现2点”的概率之和,即
P(C)=P(A)+P(B)=
例4. 在数学考试中,小明的成绩在90分以上的概率是0.18,在80~89分的概率是0.51,在70~79分的概率是0.15,在60~69分的概率是0.09,计算小明在数学考试中取得80分以上成绩的概率和小明考试及格的概率.
解: 分别记小明的成绩在90分以上,在80~89分,在70~79分,在60~69分为事件B,C,D,E,这四个事件是彼此互斥的.
根据概率的加法公式,小明的考试成绩在80分以上的概率是
P(B∪C)=P(B)+P(C)=0.18+0.51=0.69.
小明考试及格的概率为
P(B∪C∪D∪E)=P(B)+P(C)+ P(D)+P(E)
= 0.18+0.51+0.15+0.09=0.93.
对立事件的概率
若事件A的对立事件为A,则
P(A)=1-P(A).
证明:事件A与A是互斥事件,所以P(A∪A)=P(A)+P(A),又A∪A=Ω,
而由必然事件得到P(Ω)=1,
故P(A)=1-P(A).
在上面的例题中,若令A=“小明考试及格”,则A=“小明考试不及格”
如果求小明考试不及格的概率,则由公式得
P(A)=1-P(A)=1-0.93=0.07.
即小明考试不及格的概率是0.07.
例5. 某战士射击一次,问:
(1)若事件A=“中靶”的概率为0.95,则A的概率为多少?
(2)若事件B=“中靶环数大于5”的概率为0.7 ,那么事件C=“中靶环数小于6”的概率为多少?
(3)事件D=“中靶环数大于0且小于6”的概率是多少?
解:因为A与A互为对立事件,
(1)P(A)=1-P(A)=0.05;
(2)事件B与事件C也是互为对立事件,
所以P(C)=1-P(B)=0.3;
(3)事件D的概率应等于中靶环数小于6的概率减去未中靶的概率,即
P(D)=P(C)-P(A)=0.3-0.05=0.25
例6.盒内装有各色球12只,其中5红、4黑、2白、1绿,从中取1球,设事件A为“取出1只红球”,事件B为“取出1只黑球”,事件C为“取出1只白球”,事件D为“取出1只绿球”.已知P(A)= ,P(B)= , P(C)= ,P(D)= ,
求:(1)“取出1球为红或黑”的概率;(2)“取出1球为红或黑或白”的概率.
解:(1)“取出红球或黑球”的概率为P(A∪B)=P(A)+P(B)= ;
(2)“取出红或黑或白球”的概率为P(A∪B∪C)=P(A)+P(B)+P(C)= 。
又(2)A∪B∪C的对立事件为D,
所以P(A∪B∪C)=1-P(D)= 即为所求.
例7. 某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3、0.2、0.1、0.4,
(1)求他乘火车或乘飞机去的概率;
(2)求他不乘轮船去的概率;
(3)如果他乘某种交通工具去开会的概率为0.5,请问他有可能是乘何种交通工具去的?
解:记“他乘火车去”为事件A,,“他乘轮船去”为事件B,“他乘汽车去”为事件C,“他乘飞机去”为事件D,这四个事件不可能同时发生,故它们彼此互斥,
(1)故P(A∪C)=0.4;
(2)设他不乘轮船去的概率为P,则P=1-P(B)=0.8;
(3)由于0.5=0.1+0.4=0.2+0.3,故他有可能乘火车或乘轮船去,也有可能乘汽车或乘飞机去。
练习题:
1.每道选择题有4个选择项,其中只有1个选择项是正确的。某次考试共有12道选择题,某人说:“每题选择正确的概率是1/4,我每题都选择第一个选择项,则一定有3题选择结果正确”这句话( )
(A)正确 (B)错误
(C)不一定 (D)无法解释
B
2.从1,2,…,9中任取两数,其中:①恰有一个偶数和恰有一个奇数;②至少有一个奇数和两个都是奇数;③至少有一个奇数和两个都是偶数;④至少有一个奇数和至少有一个偶数。在上述事件中,是对立事件的是( )
(A)① (B)②④
(C)③ (D)①③
C
3.甲、乙2人下棋,下成和棋的概率是 ,乙获胜的概率是 ,则甲不胜的概率是( )
A. B.
C. D.
B
4. 从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“至少有一个红球”
C.“恰有一个黑球”与“恰有两个黑球”
D.“至少有一个黑球”与“都是红球”
C
5.抽查10件产品,设事件A:至少有两件次品,则A的对立事件为( )
A. 至多两件次品
B. 至多一件次品
C. 至多两件正品
D. 至少两件正品
B
6. 从一批羽毛球产品中任取一个,其质量小于4.8 g的概率为0.3,质量小于4.85 g的概率为0.32,那么质量在[4.8,4.85) (g)范围内的概率是 ( )
A.0.62 B.0.38
C.0.02 D.0.68
C
7.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03、丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为( )
A.0.09 B.0.98
C.0.97 D.0.96
D
8.某射手射击一次击中10环、9环、8环的概率分别是0.3,0.3,0.2,那么他射击一次不够8环的概率是 。
0.2
9. 某人在打靶中,连续射击2次,事件“至少有一次中靶”的互斥事件是 .
两次都不中靶
10. 我国西部一个地区的年降水量在下列区间内的概率如下表所示:
年降水量/mm [100,150) [150,200) [200,250) [250,300]
概率 0.21 0.16 0.13 0.12
则年降水量在[200,300](mm)范围内的概率是______________.
0.25
11.某射手在一次射击中射中10环、9环、8环、7环、7环以下的概率分别为0.24、0.28、0.19、0.16、0.13.计算这个射手在一次射击中:
(1)射中10环或9环的概率,
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.
0.52
0.87
0.29
3.1.4 概率的加法公式
一、互斥事件、事件的并、对立事件
1.互斥事件:不可能同时发生的两个事件叫做互斥事件(或称为互不相容事件);
2.事件的并:由事件A和B至少有一个发生(即A发生,或B发生,或A、B都发生)所构成的事件C,称为事件A与B的并(或和)。记作C=A∪B(或C=A+B)。
事件A∪B是由事件A或B所包含的基本事件所组成的集合。
3.对立事件:不能同时发生且必有一个发生的两个事件叫做互为对立事件。
事件A的对立事件记作.
例1. 抛掷一颗骰子,观察掷出的点数. 设事件A为“出现奇数点”,B为“出现2点”. 已知P(A)= ,P(B)= ,求“出现奇数点或2点”的概率。
这里的事件A和事件B不可能同时发生,这种不可能同时发生的两个事件叫做互斥事件
设事件C为““出现奇数点”或2点”,它也是一个随机事件。
事件C与事件A、B的关系是:若事件A和事件B中至少有一个发生,则C发生;若C发生,则A,B中至少有一个发生,我们称事件C为A与B的并(或和)
设事件C为““出现奇数点”或2点”,它也是一个随机事件。
事件C与事件A、B的关系是:若事件A和事件B中至少有一个发生,则C发生;若C发生,则A,B中至少有一个发生,我们称事件C为A与B的并(或和)
如图中阴影部分所表示的就是A∪B.
例2.判断下列各对事件是否是互斥事件,并说明理由。
某小组有3名男生和2名女生,从中任选2名同学去参加演讲比赛,其中
(1)恰有1名男生和恰有2名男生;
(2)至少有1名男生和至少有1名女生;
(3)至少有1名男生和全是男生;
(4)至少有1名男生和全是女生。
解:(1)是互斥事件;
(2)不可能是互斥事件;
(3)不可能是互斥事件;
(4)是互斥事件;
例3.判断下列给出的每对事件,(1)是否为互斥事件,(2)是否为对立事件,并说明理由。
从40张扑克牌(红桃、黑桃、方块、梅花,点数从1~10各4张)中,任取1张:
(1)“抽出红桃”与“抽出黑桃”;
(2)“抽出红色牌”与“抽出黑色牌”;
(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”。
解:(1)是互斥事件,不是对立事件;
(2)既是互斥事件,又是对立事件;
(3)不是互斥事件,当然不可能是对立事件;
所以对立事件一定是互斥事件,而互斥事件不一定是对立事件。
假定事件A与B互斥,则
P(A∪B)=P(A)+P(B)。
二、互斥事件的概率加法公式
证明:假定A、B为互斥事件,在n次试验中,事件A出现的频数为n1,事件B出现的频数为n2,则事件A∪B出现的频数正好是n1+n2,所以事件A∪B的频率为
如果用μn(A)表示在n次试验中事件A出现的频率,则有μn(A∪B)=μn(A)+μn(B).
由概率的统计定义可知,
P(A∪B)=P(A)+P(B)。
一般地,如果事件A1,A2,…,An彼此互斥,那么P(A1∪A2∪…∪An)=P(A1)+P(A2) +…+P(An),即彼此互斥事件和的概率等于概率的和.
在求某些较为复杂事件的概率时,先将它分解为一些较为简单的、并且概率已知(或较容易求出)的彼此互斥的事件,然后利用概率的加法公式求出概率. 因此互斥事件的概率加法公式具有“化整为零、化难为易”的功效,但需要注意的是使用该公式时必须检验是否满足它的前提条件“彼此互斥”.
例1中事件C:“出现奇数点或2点”的概率是事件A:“出现奇数点”的概率与事件B:“出现2点”的概率之和,即
P(C)=P(A)+P(B)=
例4. 在数学考试中,小明的成绩在90分以上的概率是0.18,在80~89分的概率是0.51,在70~79分的概率是0.15,在60~69分的概率是0.09,计算小明在数学考试中取得80分以上成绩的概率和小明考试及格的概率.
解: 分别记小明的成绩在90分以上,在80~89分,在70~79分,在60~69分为事件B,C,D,E,这四个事件是彼此互斥的.
根据概率的加法公式,小明的考试成绩在80分以上的概率是
P(B∪C)=P(B)+P(C)=0.18+0.51=0.69.
小明考试及格的概率为
P(B∪C∪D∪E)=P(B)+P(C)+ P(D)+P(E)
= 0.18+0.51+0.15+0.09=0.93.
对立事件的概率
若事件A的对立事件为A,则
P(A)=1-P(A).
证明:事件A与A是互斥事件,所以P(A∪A)=P(A)+P(A),又A∪A=Ω,
而由必然事件得到P(Ω)=1,
故P(A)=1-P(A).
在上面的例题中,若令A=“小明考试及格”,则A=“小明考试不及格”
如果求小明考试不及格的概率,则由公式得
P(A)=1-P(A)=1-0.93=0.07.
即小明考试不及格的概率是0.07.
例5. 某战士射击一次,问:
(1)若事件A=“中靶”的概率为0.95,则A的概率为多少?
(2)若事件B=“中靶环数大于5”的概率为0.7 ,那么事件C=“中靶环数小于6”的概率为多少?
(3)事件D=“中靶环数大于0且小于6”的概率是多少?
解:因为A与A互为对立事件,
(1)P(A)=1-P(A)=0.05;
(2)事件B与事件C也是互为对立事件,
所以P(C)=1-P(B)=0.3;
(3)事件D的概率应等于中靶环数小于6的概率减去未中靶的概率,即
P(D)=P(C)-P(A)=0.3-0.05=0.25
例6.盒内装有各色球12只,其中5红、4黑、2白、1绿,从中取1球,设事件A为“取出1只红球”,事件B为“取出1只黑球”,事件C为“取出1只白球”,事件D为“取出1只绿球”.已知P(A)= ,P(B)= , P(C)= ,P(D)= ,
求:(1)“取出1球为红或黑”的概率;(2)“取出1球为红或黑或白”的概率.
解:(1)“取出红球或黑球”的概率为P(A∪B)=P(A)+P(B)= ;
(2)“取出红或黑或白球”的概率为P(A∪B∪C)=P(A)+P(B)+P(C)= 。
又(2)A∪B∪C的对立事件为D,
所以P(A∪B∪C)=1-P(D)= 即为所求.
例7. 某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为0.3、0.2、0.1、0.4,
(1)求他乘火车或乘飞机去的概率;
(2)求他不乘轮船去的概率;
(3)如果他乘某种交通工具去开会的概率为0.5,请问他有可能是乘何种交通工具去的?
解:记“他乘火车去”为事件A,,“他乘轮船去”为事件B,“他乘汽车去”为事件C,“他乘飞机去”为事件D,这四个事件不可能同时发生,故它们彼此互斥,
(1)故P(A∪C)=0.4;
(2)设他不乘轮船去的概率为P,则P=1-P(B)=0.8;
(3)由于0.5=0.1+0.4=0.2+0.3,故他有可能乘火车或乘轮船去,也有可能乘汽车或乘飞机去。
练习题:
1.每道选择题有4个选择项,其中只有1个选择项是正确的。某次考试共有12道选择题,某人说:“每题选择正确的概率是1/4,我每题都选择第一个选择项,则一定有3题选择结果正确”这句话( )
(A)正确 (B)错误
(C)不一定 (D)无法解释
B
2.从1,2,…,9中任取两数,其中:①恰有一个偶数和恰有一个奇数;②至少有一个奇数和两个都是奇数;③至少有一个奇数和两个都是偶数;④至少有一个奇数和至少有一个偶数。在上述事件中,是对立事件的是( )
(A)① (B)②④
(C)③ (D)①③
C
3.甲、乙2人下棋,下成和棋的概率是 ,乙获胜的概率是 ,则甲不胜的概率是( )
A. B.
C. D.
B
4. 从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球”
B.“至少有一个黑球”与“至少有一个红球”
C.“恰有一个黑球”与“恰有两个黑球”
D.“至少有一个黑球”与“都是红球”
C
5.抽查10件产品,设事件A:至少有两件次品,则A的对立事件为( )
A. 至多两件次品
B. 至多一件次品
C. 至多两件正品
D. 至少两件正品
B
6. 从一批羽毛球产品中任取一个,其质量小于4.8 g的概率为0.3,质量小于4.85 g的概率为0.32,那么质量在[4.8,4.85) (g)范围内的概率是 ( )
A.0.62 B.0.38
C.0.02 D.0.68
C
7.某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03、丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为( )
A.0.09 B.0.98
C.0.97 D.0.96
D
8.某射手射击一次击中10环、9环、8环的概率分别是0.3,0.3,0.2,那么他射击一次不够8环的概率是 。
0.2
9. 某人在打靶中,连续射击2次,事件“至少有一次中靶”的互斥事件是 .
两次都不中靶
10. 我国西部一个地区的年降水量在下列区间内的概率如下表所示:
年降水量/mm [100,150) [150,200) [200,250) [250,300]
概率 0.21 0.16 0.13 0.12
则年降水量在[200,300](mm)范围内的概率是______________.
0.25
11.某射手在一次射击中射中10环、9环、8环、7环、7环以下的概率分别为0.24、0.28、0.19、0.16、0.13.计算这个射手在一次射击中:
(1)射中10环或9环的概率,
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.
0.52
0.87
0.29
