1.3.1 有理数的加法(1)课件(共17张PPT)
文档属性
| 名称 | 1.3.1 有理数的加法(1)课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 670.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 14:58:00 | ||
图片预览



文档简介
(共17张PPT)
人教版 七年级上
1.3.1有理数的加法(1)
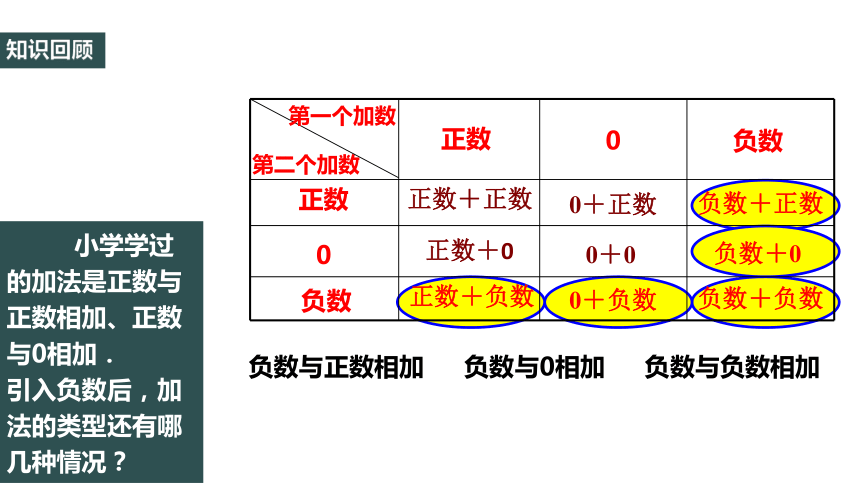
小学学过的加法是正数与正数相加、正数与0相加.
引入负数后,加法的类型还有哪几种情况?
正数+正数
0+正数
负数+正数
0+0
负数+0
0+负数
负数+负数
第二个加数
正数
0
负数
正数
0
负数
正数+0
正数+负数
第一个加数
负数与负数相加
负数与正数相加
负数与0相加
知识回顾
重点:了解有理数的加法的意义,会根据有理数的加法法则进行有理数的加法运算
难点:有理数加法中的异号两数如何进行加法运算
重点难点
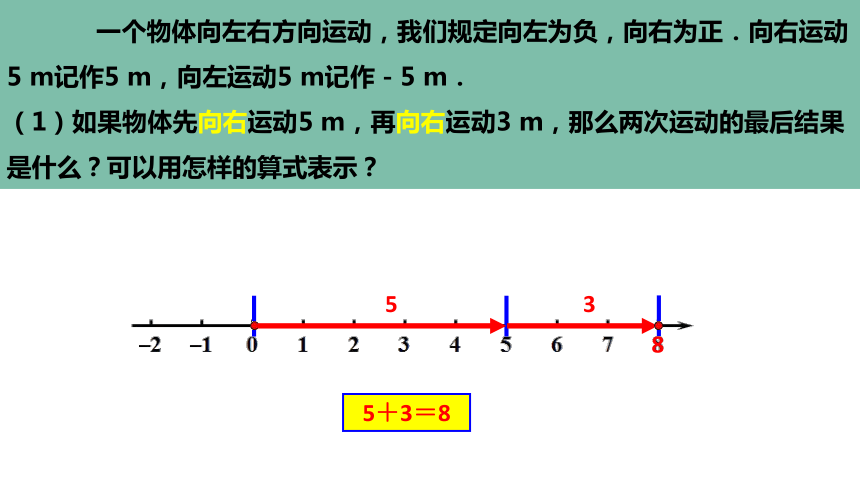
一个物体向左右方向运动,我们规定向左为负,向右为正.向右运动5 m记作5 m,向左运动5 m记作-5 m.
(1)如果物体先向右运动5 m,再向右运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
5
3
8
5+3=8
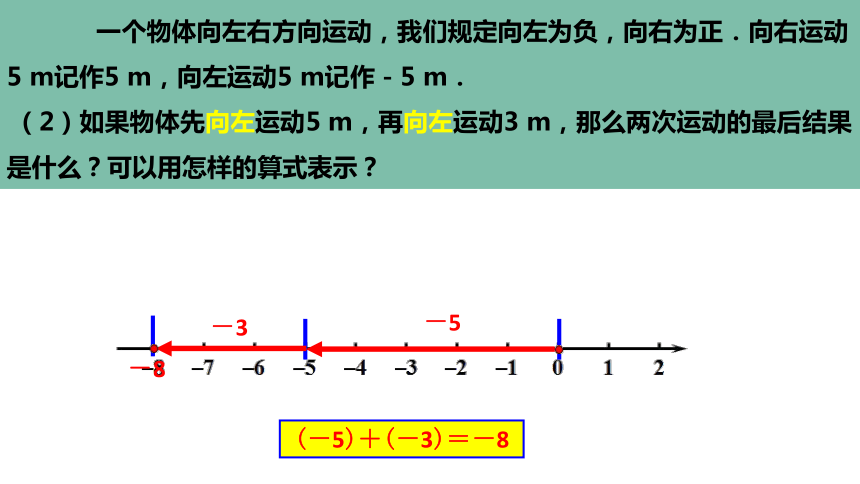
一个物体向左右方向运动,我们规定向左为负,向右为正.向右运动5 m记作5 m,向左运动5 m记作-5 m.
(2)如果物体先向左运动5 m,再向左运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
-5
-3
-8
(-5)+(-3)=-8
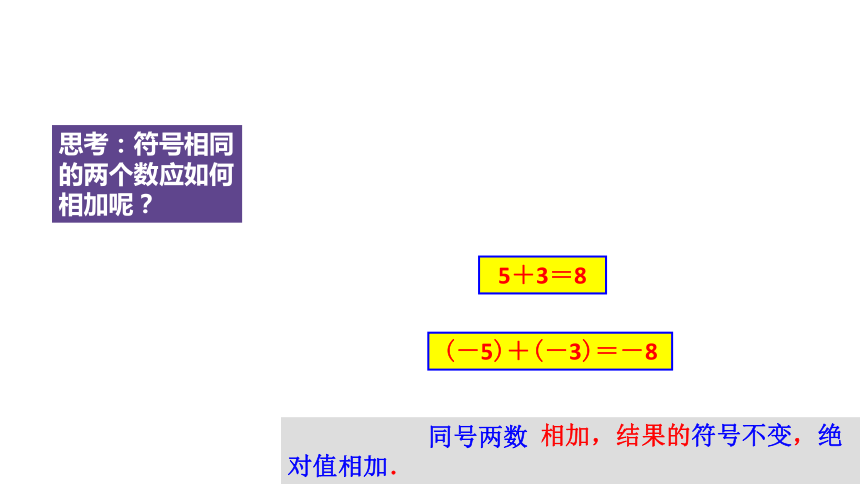
(-5)+(-3)=-8
5+3=8
思考:符号相同的两个数应如何相加呢?
符号相同的两个数相加,结果的符号不变,绝对值相加.
同号两数
1.判断对错,并说明理由.
(1)-5+6=-11 ( )
(2)(-2)+(-5)=3 ( )
(3)(-8)+(-6)=-14 ( )
2. 填空.
×
×
√
7+5=_____, (-2)+(-6)=______.
12
-8
变式训练
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
例题讲解
例1: 计算:
(1)(-3)+(-9);
(2)(-4.7)+3.9;
解:
(1)(-3)+(-9)
=-( 3+9)
=-12
先定符号,
再算绝对值.
(2)(-4.7)+3.9
=-(4.7-3.9)
=-0.8
变式训练
(1)(+9)+(-2); (2)(-9)+(+2);
(3)(-9)+0; (4)0+(+2);
答案:(1 ) 7 ; (2)-7; (3 ) -9; (4)2
课堂练习
1. 有理数加法法则:
(1)同号两数相加,取相同的符号,并把 相加;
(2)绝对值不相等的 两数相加,取绝对值 的加数的符号,并用较大的绝对值 较小的绝对值;互为相反数的两个数相加得 ;
(3)一个数同 相加,仍得这个数.
2. 两数相加时,首先确定 的符号,再确定 的大小,最后将绝对值相加或相减.
绝对值
异号
较大
减去
0
0
和
绝对值
3. 在1,-1,-2这3个数中,任意两数之和的最大值是( )
A. 1 B. 0 C. -1 D. 3
B
4.计算:
(1) (-7)+(-3); (2)(-40)+(+15)
(3)10+(-3); (4)(+9)+7
(5)(-15)+(-20);(6)(-9)+ 0
(7)100+(-99) ; (8)(-0.5)+ 4.4
(1)-10;(2)-25;(3)7;(4)16;
答案:
(5)-35;(6)-9; (7)1;(8)3.9
5. 根据题意列式计算:
(1)比-10的相反数大-20的数;
(2)16的相反数与-8的绝对值的和;
(3)m是绝对值最小的数,n是最大的负整数,p是最小的正整数,求m+n+(-p)的值.
解:(1)-(-10)+(-20)=-10.
(2)(-16)+|-8|=-8.
(3)由题意得,m=0,n=-1,p=1,
所以m+n+(-p)=0+(-1)+(-1)=-2.
课堂总结
今天我们学习了哪些知识?
1.有理数的加法法则是什么?
2.进行有理数的加法运算时需要注意哪几个步骤?
教材p18练习题.
课后作业
谢
谢
观
看
人教版 七年级上
1.3.1有理数的加法(1)
小学学过的加法是正数与正数相加、正数与0相加.
引入负数后,加法的类型还有哪几种情况?
正数+正数
0+正数
负数+正数
0+0
负数+0
0+负数
负数+负数
第二个加数
正数
0
负数
正数
0
负数
正数+0
正数+负数
第一个加数
负数与负数相加
负数与正数相加
负数与0相加
知识回顾
重点:了解有理数的加法的意义,会根据有理数的加法法则进行有理数的加法运算
难点:有理数加法中的异号两数如何进行加法运算
重点难点
一个物体向左右方向运动,我们规定向左为负,向右为正.向右运动5 m记作5 m,向左运动5 m记作-5 m.
(1)如果物体先向右运动5 m,再向右运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
5
3
8
5+3=8
一个物体向左右方向运动,我们规定向左为负,向右为正.向右运动5 m记作5 m,向左运动5 m记作-5 m.
(2)如果物体先向左运动5 m,再向左运动3 m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
-5
-3
-8
(-5)+(-3)=-8
(-5)+(-3)=-8
5+3=8
思考:符号相同的两个数应如何相加呢?
符号相同的两个数相加,结果的符号不变,绝对值相加.
同号两数
1.判断对错,并说明理由.
(1)-5+6=-11 ( )
(2)(-2)+(-5)=3 ( )
(3)(-8)+(-6)=-14 ( )
2. 填空.
×
×
√
7+5=_____, (-2)+(-6)=______.
12
-8
变式训练
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
例题讲解
例1: 计算:
(1)(-3)+(-9);
(2)(-4.7)+3.9;
解:
(1)(-3)+(-9)
=-( 3+9)
=-12
先定符号,
再算绝对值.
(2)(-4.7)+3.9
=-(4.7-3.9)
=-0.8
变式训练
(1)(+9)+(-2); (2)(-9)+(+2);
(3)(-9)+0; (4)0+(+2);
答案:(1 ) 7 ; (2)-7; (3 ) -9; (4)2
课堂练习
1. 有理数加法法则:
(1)同号两数相加,取相同的符号,并把 相加;
(2)绝对值不相等的 两数相加,取绝对值 的加数的符号,并用较大的绝对值 较小的绝对值;互为相反数的两个数相加得 ;
(3)一个数同 相加,仍得这个数.
2. 两数相加时,首先确定 的符号,再确定 的大小,最后将绝对值相加或相减.
绝对值
异号
较大
减去
0
0
和
绝对值
3. 在1,-1,-2这3个数中,任意两数之和的最大值是( )
A. 1 B. 0 C. -1 D. 3
B
4.计算:
(1) (-7)+(-3); (2)(-40)+(+15)
(3)10+(-3); (4)(+9)+7
(5)(-15)+(-20);(6)(-9)+ 0
(7)100+(-99) ; (8)(-0.5)+ 4.4
(1)-10;(2)-25;(3)7;(4)16;
答案:
(5)-35;(6)-9; (7)1;(8)3.9
5. 根据题意列式计算:
(1)比-10的相反数大-20的数;
(2)16的相反数与-8的绝对值的和;
(3)m是绝对值最小的数,n是最大的负整数,p是最小的正整数,求m+n+(-p)的值.
解:(1)-(-10)+(-20)=-10.
(2)(-16)+|-8|=-8.
(3)由题意得,m=0,n=-1,p=1,
所以m+n+(-p)=0+(-1)+(-1)=-2.
课堂总结
今天我们学习了哪些知识?
1.有理数的加法法则是什么?
2.进行有理数的加法运算时需要注意哪几个步骤?
教材p18练习题.
课后作业
谢
谢
观
看
