1.3.1 有理数的加法(2)课件(共18张PPT)
文档属性
| 名称 | 1.3.1 有理数的加法(2)课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-12 14:58:00 | ||
图片预览






文档简介
(共18张PPT)
人教版
七上
1.3.1
有理数的加法(2)
有理数的加法法则是什么?
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
知识回顾
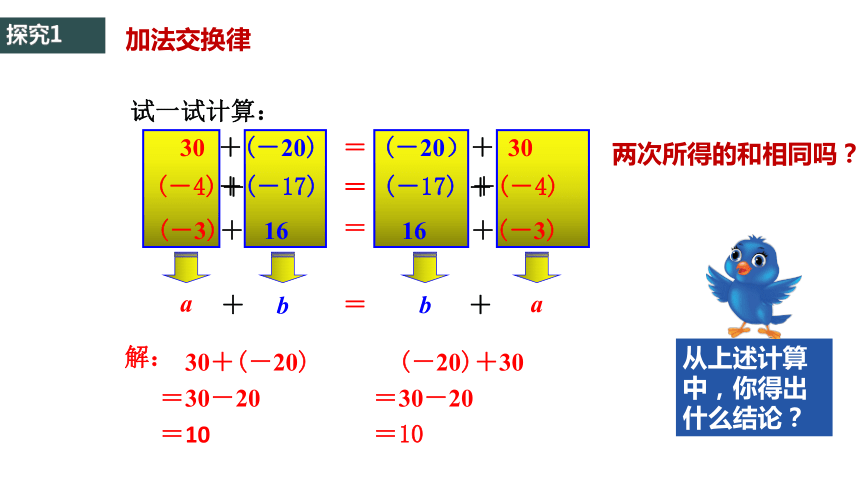
解:
30+(-20)
=30-20
=10
(-20)+30
=30-20
=10
=
=
=
a
a
b
b
+
+
+
+
=
=
试一试计算:
30
+(-20)
(-20)+
30
(-4)+(-17)
(-17)
+(-4)
(-3)+
16
16
+(-3)
加法交换律
探究1
从上述计算中,你得出什么结论?
两次所得的和相同吗?
有理数加法中,两个数相加,交换加数的位置,和不变.
加法交换律:a+b=b+a
计算:
[8+(-5)]+(-4)
8+[(-5)+(-4)]
解:[8+(-5)]+(-4)
=3+(-4)
=-1
8+[(-5)+(-4)]
=8+(-9)
=-1
=
两次所得的和相同吗?
探究2
加法结合律
计算:
[8+(-5)]+(-4)
8+[(-5)+(-4)]
=
你能得出什么结论呢?
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律:(a+b)+c=a+(b+c)
例题讲解
例2
计算16
+
(-25)
+
24+
(-35).
解:
16
+
(-25)
+
24+
(-35)
=
16
+
24
+
[
(-25)
+
(-35)]
=40+
(-60)
=-20.
本例中是怎样使计算简化的?根据是什么?
把正数或负数分别相加,从而使计算简化.
计算:43+(-77)+37+(-23).
导引:
先把正数、负数分别结合,然后再计算.
解:
原式=(43+37)+[(-77)+(-23)]
=80+(-100)
=-20.
变式练习
例题讲解
例3
10袋小麦称后记录如图所示(单位:kg).
10袋
小麦一共多
少千克?如果每袋小麦以90
kg为标准,10袋小麦总计超过多少千克或不足多少千克?
解法1:先计算10袋小麦一共多少千克:
91
+
91
+
91.
5+89
+
91.
2
+
91.
3+88.
7+88.
8+
91.
8+91.
1
=
905.
4.
再计算总计超过多少千克:
905.4-90×10=5.
4.
解法二:每袋小麦超过90kg的记作正数,不足的记作负数.
10袋小麦对应的分别为:
+1,+1,+1.5,
-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4
90×10+5.4=905.4.
答:10袋小麦一共905.4千克,总计超过5.4千克.
1.
加法交换律:两个数相加,交换
的位置,
不变,用字母表示为a+b=
.
2.
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,
不变,用字母表示为(a+b)+c=
.
3.
常用组合方法:相反数结合法;同号结合法;同分母结合法;凑整法;同形结合法等。
课堂练习
加数
和
b+a
和
a+(b+c)
4.
下列变形运用加法运算律正确的是( )
4+(-3)=4+3
B.
2+(-5)+4=(-5)+4+2
C.
[-3+(-2)]+5=[-3+(-5)]+2
D.+(-1)
+(+)
=+
+
(+1)
B
课堂练习
5.计算
(1)10+(-24)+(-5)+26+(-42)+18;
原式=(10+26+18)-(24+5+42)
=54-71
=-17.
6.有6筐蔬菜,每筐质量分别为(单位:kg):
48,52,47,49,53,54.
(1)如果以50kg为基准,超过的千克数记为正数,不足的千克数记为负数,则用正、负数表示这6筐蔬菜的质量分别为(单位:kg):
_____,_____,_____,_____,_____,_____;
(2)试用两种不同的方法求出这6筐蔬菜的总质量.
-2
+2
-3
-1
+3
+4
解:(2)方法一:48+52+47+49+53+54=303;
方法二:
(-2)+(+2)+(-3)+(-1)+(+3)+(+4)=3
50×6
+3
=300+3=303
答:这6筐蔬菜的总质量是303kg.
有理数的加法运算律及其应用:
①先将相反数相加;
②再将其中的同号的数相加;
③最后求异号加数的和,有分数时,可把相加得整数的先加起来.
加法交换律:
加法结合律:
a
+
b
=
b
+
a
a+(
b+
c
)=(
a
+b
)+c
本节课里我的收获是……
课堂总结
P20教材练习题1—2题.
课后作业
https://www.21cnjy.com/help/help_extract.php
人教版
七上
1.3.1
有理数的加法(2)
有理数的加法法则是什么?
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
知识回顾
解:
30+(-20)
=30-20
=10
(-20)+30
=30-20
=10
=
=
=
a
a
b
b
+
+
+
+
=
=
试一试计算:
30
+(-20)
(-20)+
30
(-4)+(-17)
(-17)
+(-4)
(-3)+
16
16
+(-3)
加法交换律
探究1
从上述计算中,你得出什么结论?
两次所得的和相同吗?
有理数加法中,两个数相加,交换加数的位置,和不变.
加法交换律:a+b=b+a
计算:
[8+(-5)]+(-4)
8+[(-5)+(-4)]
解:[8+(-5)]+(-4)
=3+(-4)
=-1
8+[(-5)+(-4)]
=8+(-9)
=-1
=
两次所得的和相同吗?
探究2
加法结合律
计算:
[8+(-5)]+(-4)
8+[(-5)+(-4)]
=
你能得出什么结论呢?
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律:(a+b)+c=a+(b+c)
例题讲解
例2
计算16
+
(-25)
+
24+
(-35).
解:
16
+
(-25)
+
24+
(-35)
=
16
+
24
+
[
(-25)
+
(-35)]
=40+
(-60)
=-20.
本例中是怎样使计算简化的?根据是什么?
把正数或负数分别相加,从而使计算简化.
计算:43+(-77)+37+(-23).
导引:
先把正数、负数分别结合,然后再计算.
解:
原式=(43+37)+[(-77)+(-23)]
=80+(-100)
=-20.
变式练习
例题讲解
例3
10袋小麦称后记录如图所示(单位:kg).
10袋
小麦一共多
少千克?如果每袋小麦以90
kg为标准,10袋小麦总计超过多少千克或不足多少千克?
解法1:先计算10袋小麦一共多少千克:
91
+
91
+
91.
5+89
+
91.
2
+
91.
3+88.
7+88.
8+
91.
8+91.
1
=
905.
4.
再计算总计超过多少千克:
905.4-90×10=5.
4.
解法二:每袋小麦超过90kg的记作正数,不足的记作负数.
10袋小麦对应的分别为:
+1,+1,+1.5,
-1,+1.2,+1.3,-1.3,-1.2,+1.8,+1.1
1+1+1.5+(-1)+1.2+1.3+(-1.3)+(-1.2)+1.8+1.1
=[1+(-1)]+[1.2+(-1.2)]+[1.3+(-1.3)]+(1+1.5+1.8+1.1)
=5.4
90×10+5.4=905.4.
答:10袋小麦一共905.4千克,总计超过5.4千克.
1.
加法交换律:两个数相加,交换
的位置,
不变,用字母表示为a+b=
.
2.
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,
不变,用字母表示为(a+b)+c=
.
3.
常用组合方法:相反数结合法;同号结合法;同分母结合法;凑整法;同形结合法等。
课堂练习
加数
和
b+a
和
a+(b+c)
4.
下列变形运用加法运算律正确的是( )
4+(-3)=4+3
B.
2+(-5)+4=(-5)+4+2
C.
[-3+(-2)]+5=[-3+(-5)]+2
D.+(-1)
+(+)
=+
+
(+1)
B
课堂练习
5.计算
(1)10+(-24)+(-5)+26+(-42)+18;
原式=(10+26+18)-(24+5+42)
=54-71
=-17.
6.有6筐蔬菜,每筐质量分别为(单位:kg):
48,52,47,49,53,54.
(1)如果以50kg为基准,超过的千克数记为正数,不足的千克数记为负数,则用正、负数表示这6筐蔬菜的质量分别为(单位:kg):
_____,_____,_____,_____,_____,_____;
(2)试用两种不同的方法求出这6筐蔬菜的总质量.
-2
+2
-3
-1
+3
+4
解:(2)方法一:48+52+47+49+53+54=303;
方法二:
(-2)+(+2)+(-3)+(-1)+(+3)+(+4)=3
50×6
+3
=300+3=303
答:这6筐蔬菜的总质量是303kg.
有理数的加法运算律及其应用:
①先将相反数相加;
②再将其中的同号的数相加;
③最后求异号加数的和,有分数时,可把相加得整数的先加起来.
加法交换律:
加法结合律:
a
+
b
=
b
+
a
a+(
b+
c
)=(
a
+b
)+c
本节课里我的收获是……
课堂总结
P20教材练习题1—2题.
课后作业
https://www.21cnjy.com/help/help_extract.php
